«Солнце в зените» — что значит это выражение? Как понять, что солнце находится в зените
Часто можно услышать выражение «солнце в зените». Что это значит? Где, в какой точке небосвода можно увидеть светило в этот момент, и как такая позиция отличается от других его положений и состояний? В какое время суток или года это происходит? И, если солнце в зените — что это значит для жителей планеты Земля?
Основные сведения о Солнце
Солнце — это ближайшая звезда к планете Земля, центральное небесное тело одноименной системы, имеющее форму шара и состоящее из раскаленных газов с температурой поверхности приближенной к 5505°C, а в центральной части разогретое до 13,5 миллионов градусов.
В диаметре Солнце почти в 110 раз больше планеты Земля — 1 392 000 километров.
Вокруг Солнца имеется атмосфера, состоящая из трех слоев — фотосферы, хромосферы и солнечной короны. Все излучение, которое люди могут воспринять с помощью зрения, относится к первому слою. Во время полного солнечного затмения можно наблюдать солнечную корону, которая в диаметре в разы превосходит свой источник.
Масса Солнца превышает земную в 333 тысячи раз, но его объем еще больше — в 1 миллион 304 тысячи раз, что значит меньшую плотность состава звезды.
Энергия, получаемая нашей планетой от Солнца, составляет лишь малую часть всей, излучаемой звездой, но она многократно превышает всю, вырабатываемую на Земле искусственно.
Оборот солнца вокруг своей оси происходит за 25,4 привычных нам двадцатичетырехчасовых суток.
Примерное расстояние от нашей планеты до Солнца — 149,5 миллионов километров, но эти величины так огромны с точки зрения преодоления, что меряются не линейными единицами, а временными с позиции движения света. Солнечный свет достигает Земли за 8 минут и 18 секунд (скорость его перемещения равна 300 000 километрам в секунду).
Вся Солнечная система постоянно смещается в космическом пространстве по направлению к созвездию Лиры. Скорость этого движения равна 20 километрам в секунду.
Что такое зенит?
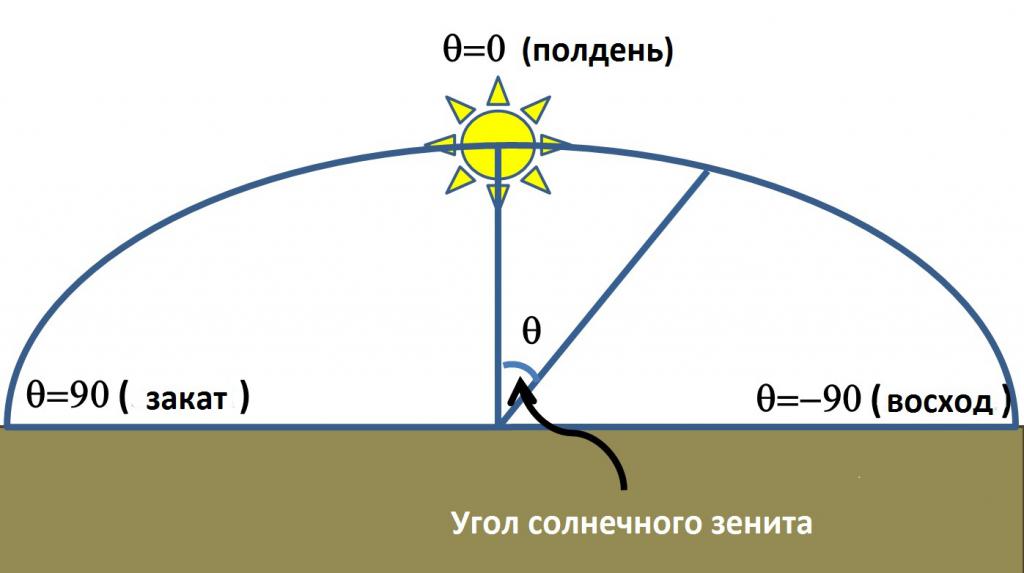
Зенитом называют наивысшую точку на небосводе, то есть, когда говорят о том, что солнце в зените — это значит, что светило расположено прямо по вертикали над головой наблюдающего. Солнечные лучи в таком случае падают перпендикулярно к поверхности земли — под прямым углом. Так что, если предметы не отбрасывают тени — это значит, что солнце в зените.
Однако данное определение в разговорной речи применяется в отношении положения солнца, которое только условно можно назвать зенитом. Благодаря особенностям небесных тел и их положения в космическом пространстве относительно друг друга, падать под углом, равным 90°, лучи Солнца будут далеко не на каждую часть Земли.
Точка, находящаяся на этой же отвесной прямой, что и зенит, но в противоположном ее направлении — ниже линии горизонта, называется надиром.
Движение солнечного зенита в течение года
Так как происходит постоянное перемещение небесных тел относительно друг друга и собственной оси каждого, зенит солнца на протяжении всего земного года все время сдвигается в направлении от тропика к тропику со скоростью округленно равной 1° за четверо суток (точнее — 3,8), что в пересчете на неделю составит 2°. Это значит, что определить, как солнце в зените будет смещаться в отношении земли, очень просто.
Имея для отправной точки знания о днях солнцестояния, можно приблизительно посчитать широту, на которой солнце будет достигать своего зенита для любой даты.
Дважды в год Солнце находится в зените над экватором — 21 марта и 23 сентября в те календарные дни, когда света и тьмы в сутках поровну — это осеннее и весеннее равноденствие. Значит в расчетах широты нахождения солнца в зените это те исходные числа, которые можно брать за основу.
Например: рассчитывая широту, на которой будет солнце в российский День космонавтики — 12 апреля, необходимо определить количество суток, прошедших с ближайшей опорной даты (это будет весеннее равноденствие 21 марта). Между отправной точкой во времени и расчетной 22 календарных дня. Если смещение светила на 1° происходит за 3,8, суток, то за 22 его нахождение изменится на 22 : 3,8 = 5,7°. Так как в данном случае нет необходимости в точных вычислениях, можно округлить полученное значение до 6° — именно так изменится угол Солнца по отношению к Земле в направлении его движения к северу от экватора.
Где на нашей планете можно увидеть солнце в зените
Для удобства определения точек и положений объектов в масштабе планеты, вся Земля разделена по горизонтали и вертикали условными линиями — опоясывающие называются параллелями, и экватор, находящийся посередине, является самой длинной из них. Говоря о положении какой-то точки на планете с помощью параллелей, используют термин «широта».
Вертикальные линии — меридианы, соответствуют долготе. Все числовые значения широты и долготы обозначаются в градусах.
Благодаря форме Земли и наклону ее оси к Солнцу на 23°, положение светила относительно нашей планеты, которое определяется как зенит, возможно далеко не для каждой ее точки. Для большинства жителей это явление недоступно.
Падение солнечных лучей под прямым углом происходит только на экваторе и в пределах тропиков — между параллелями выше и ниже (южнее и севернее) линии экватора.
Северный (названный в честь созвездия Рака) и Южный (именуемый в честь Козерога) тропики условно ограничивают ту часть планеты, над которой в полдень возможно положение солнца в зените.
В день летнего солнцестояния — 22 июня, солнце в зените будет над параллелью, именуемой Северным тропиком, а в день зимнего солнцестояния, 21 декабря — над Южным. На всех широтах, расположенных между ними, положение солнца в зените можно наблюдать дважды в году.
Как солнце в наивысшей точке небосвода вдохновляет поэтов
Небесные светила, оба — и царствующее днем, и главенствующее ночью — вдохновляют людей искусства на написание картин, музыки, литературных произведений разных форм.
Среди них и молодая московская поэтесса, лауреат Пушкинского молодежного фестиваля «С веком наравне» Кира Тихонова (в девичестве Данилянц).
Солнце в зените, пальто в снегу.
Вверх по улице волоку
Санки, тяжелые, как чугун,
И под общий хохот и визг
Я, разгоняясь, слетаю вниз,
В кучу барахтающихся лиц,
Огненных от мороза.
Снега как в тундре, праздник детей!
Мы настроили крепостей,
Мы на улице целый день,
В мокрой насквозь одежде.
Мы затеяли снежный бой.
Мы в темноте приходим домой,
Разгоряченные, как из парной,
Хоть выжимай и вешай!
Солнце в зените, шорты в пыли.
В куче хохочущей ребятни
Красный, с ржавчиной на руле
Старый велик несется.
Колени в зеленке, сбиты опять.
Солнце как в тропиках — тридцать пять!
Рады гоняться и догонять
Под этим палящим солнцем.
Нету айпада, планшета нет,
До первых компьютеров — десять лет.
Детство, радостное, как свет,
Помнится через дымку.
Солнце в зените. Комбинезон.
Мой старший ребенок с хмурым лицом
Снег брезгливо пинает носком
И начинающий автор родом из подмосковного города Мытищи Виктория Викольская.
Обожаю те ясные дни,
Когда солнце приходит в зенит.
И утром приходит в зенит,
И под вечер приходит в зенит
А вовсе не только в полудень.
Даже если на улице студень,
Даже если холодно людям,
Прогуляться солнце манит
Потому что приходит в зенит!
Озаряют лучи мир с утра —
Это очень даже обычно.
Но чего-то все ж необычно.
И что же тут необычно?
Так сегодня, так было вчера.
Да само то здесь столь необычно:
Что солнцу, ему безразлично,
Какая в мире пора.
Пусть любая в мире пора —
Озаряют лучи мир с утра.
Обожаю те ясные дни,
Когда солнце приходит в зенит.
Что же значит — приходит в зенит?
Это значит — на небе ни тучи,
И утром на небе ни тучи,
И под вечер на небе ни тучи.
Блеснувший на стеклышке лучик.
На древесном листике лучик.
Иль высокие мощные кручи
Озаряет тот солнечный лучик.
Даже если хмурятся тучи —
Если есть хоть один этот лучик,
То значит — не пасмурны дни.
А если не пасмурны дни,
Как бы ни был неярок тот лучик,
Он сильнее, чем хмурые тучи!
Потому что пробился сквозь тучи,
Подаренный солнцем могучим.
Если лучик пробился сквозь тучи,-
То, значит, не пасмурны дни,
Если есть хоть один этот лучик,-
Значит солнце приходит в зенит!
Пусть это не совсем верно с точки зрения науки, зато тепло и действительно солнечно.
Солнце в зените как символ
В каждом учении, опирающемся на символизм, солнцу отведено особое место. В отношении светила как знака, имеющего влияние на расшифровку сновидений, можно встретить различные трактовки в разных сборниках.
Если приснилось солнце в зените — что это значит, и как понять такое видение? Вот несколько значений сна:
- удовлетворенное честолюбие и исчерпанные (в других вариантах — безграничные) возможности сновидца;
- удачный выбор поклонников и успешное осуществление тщательно подготовленного плана личного процветания;
- счастье и вознагражденные обоснованные амбиции;
- продвижение по карьерной лестнице;
- удача во всем.
Можно сказать, что солнце способно радовать людей, согревать и дарить им свое покровительство не только днем, во время бодрствования, но и ночью, даже во сне. Не обязательно верить в тонкие связи между событиями и явлениями, пограничные научным знаниям, чтобы сбывались добрые предсказания — достаточно просто не сомневаться в хорошем и светлом предстоящем.
Источник
Положение Солнца — Position of the Sun
Положение Солнца в небе является функцией как времени и географического расположения наблюдений на земной поверхности «s. Как околоземные орбиты на Солнце на протяжении более года , Солнце , кажется, двигаться по отношению к неподвижным звездам на небесной сфере , по круговой траектории , называемой эклиптикой .
Вращение Земли вокруг своей оси вызывает суточное движение , так что кажется, что Солнце движется по небу по пути Солнца, который зависит от географической широты наблюдателя . Время, когда Солнце проходит через меридиан наблюдателя, зависит от географической долготы .
Таким образом, чтобы найти положение Солнца в данном месте в данный момент времени, можно проделать следующие три шага:
- вычислить положение Солнца в эклиптической системе координат ,
- преобразовать в экваториальную систему координат , и
- преобразовать в горизонтальную систему координат для местного времени и местоположения наблюдателя.
СОДЕРЖАНИЕ
Примерное положение
Эклиптические координаты
Эти уравнения из Астрономического альманаха можно использовать для расчета видимых координат Солнца , среднего равноденствия и эклиптики даты с точностью около 0 ° 0,01 (36 дюймов) для дат между 1950 и 2050 годами. закодированы в подпрограмму Fortran 90 в Ref. и используются для расчета зенитного угла Солнца и солнечного азимута в наблюдаемом с поверхности Земли.
Начните с вычисления n — количества дней (положительных или отрицательных, включая дробные дни) с полудня по Гринвичу по земному времени 1 января 2000 года ( J2000.0 ). Если известна юлианская дата нужного времени, то
п знак равно J D — 2451545,0 <\ displaystyle n = \ mathrm 
Средняя долгота Солнца, с поправкой на аберрации света , является:
L знак равно 280 460 ∘ + 0,9856474 ∘ п <\ displaystyle L = 280,460 ^ <\ circ>+0.9856474 ^ <\ circ>n>
Средняя аномалия Солнца ( на самом деле, Земли по своей орбите вокруг Солнца, но это удобно делать вид Солнца вокруг Земли), является:
грамм знак равно 357 528 ∘ + 0,9856003 ∘ п <\ displaystyle g = 357,528 ^ <\ circ>+0,9856003 ^ <\ circ>n>
Задайте и в диапазоне от 0 ° до 360 °, добавляя или вычитая кратные 360 ° по мере необходимости. L <\ displaystyle L> грамм <\ displaystyle g>
λ знак равно L + 1,915 ∘ грех грамм + 0,020 ∘ грех 2 грамм <\ displaystyle \ lambda = L + 1,915 ^ <\ circ>\ sin g + 0,020 ^ <\ circ>\ sin 2g>
β знак равно 0 <\ displaystyle \ beta = 0> ,
поскольку эклиптическая широта Солнца никогда не превышает 0,00033 °,
а расстояние от Солнца до Земли в астрономических единицах равно:
р знак равно 1.00014 — 0,01671 потому что грамм — 0,00014 потому что 2 грамм <\ Displaystyle R = 1.00014-0.01671 \ cos g-0.00014 \ cos 2g> .
Наклон эклиптики
Если угол наклона эклиптики нигде не получен, его можно приблизительно определить:
ϵ знак равно 23 439 ∘ — 0,0000004 ∘ п <\ displaystyle \ epsilon = 23,439 ^ <\ circ>-0,0000004 ^ <\ circ>n>
Экваториальные координаты
λ <\ displaystyle \ lambda> , и образуют полное положение Солнца в эклиптической системе координат . Это может быть превращено в экваториальной системе координат пути вычисления наклонения эклиптики , и продолжает: β <\ displaystyle \ beta> р <\ displaystyle R> ϵ <\ displaystyle \ epsilon>
α знак равно арктан ( потому что ϵ загар λ ) <\ Displaystyle \ альфа = \ arctan (\ соз \ эпсилон \ загар \ лямбда)> , где находится в том же квадранте, что и , α <\ displaystyle \ alpha> λ <\ displaystyle \ lambda>
Чтобы получить RA в правом квадранте в компьютерных программах, используйте функцию Arctan с двойным аргументом, такую как ATAN2 (y, x)
α знак равно арктан 2 ( потому что ϵ грех λ , потому что λ ) <\ Displaystyle \ альфа = \ arctan 2 (\ соз \ эпсилон \ грех \ лямбда, \ соз \ лямбда)>
δ знак равно Arcsin ( грех ϵ грех λ ) <\ Displaystyle \ дельта = \ arcsin (\ грех \ эпсилон \ грех \ лямбда)> .
Прямоугольные экваториальные координаты
Правые прямоугольные экваториальные координаты в астрономических единицах равны:
Икс знак равно р потому что λ <\ displaystyle X = R \ cos \ lambda> Y знак равно р потому что ϵ грех λ <\ Displaystyle Y = R \ соз \ эпсилон \ грех \ лямбда> Z знак равно р грех ϵ грех λ <\ Displaystyle Z = р \ грех \ эпсилон \ грех \ лямбда> Где ось находится в направлении мартовского равноденствия , ось — в сторону июньского солнцестояния , а ось — в направлении северного полюса мира . Икс <\ displaystyle X> Y <\ displaystyle Y> Z <\ displaystyle Z>
Горизонтальные координаты
Склонение Солнца с Земли
Обзор
Солнце, кажется, движется на север во время северной весны , пересекая небесный экватор в мартовское равноденствие . Его склонение достигает максимума, равного углу наклона оси Земли (23,44 °) во время июньского солнцестояния , затем уменьшается до минимума (-23,44 °) во время декабрьского солнцестояния , когда его значение является отрицательным для наклона оси. Эта вариация порождает времена года .
Линейный график склонения Солнца в течение года напоминает синусоиду с амплитудой от 23,44 °, а одна лопасти волны на несколько дней дольше , чем другие, среди других отличий.
Следующие явления произошли бы, если бы Земля была идеальной сферой , вращающейся по круговой орбите вокруг Солнца, и если бы ее ось была наклонена на 90 °, так что сама ось находилась в плоскости орбиты (аналогично Урану ). На одну дату в год, Солнце будет прямо над головой на Северный полюс , поэтому его склонение будет + 90 °. В течение следующих нескольких месяцев подсолнечная точка будет двигаться к Южному полюсу с постоянной скоростью, пересекая круги широты с постоянной скоростью, так что склонение Солнца будет линейно уменьшаться со временем. В конце концов, Солнце окажется прямо над Южным полюсом со склонением -90 °; тогда он начнёт двигаться на север с постоянной скоростью. Таким образом, график солнечного склонения, если смотреть с этой сильно наклоненной Земли, будет напоминать треугольную волну, а не синусоидальную волну, зигзагообразную между плюсами и минусами 90 °, с линейными сегментами между максимумами и минимумами.
Если осевой наклон на 90 ° уменьшается, то абсолютные максимальное и минимальное значения наклона уменьшатся, чтобы равняться осевому наклону. Кроме того, формы максимумов и минимумов на графике станут менее острыми, изогнувшись, чтобы напоминать максимумы и минимумы синусоидальной волны. Однако даже когда осевой наклон равен наклону реальной Земли, максимумы и минимумы остаются более острыми, чем у синусоидальной волны.
На самом деле, орбита Земли является эллиптической . Земля движется вокруг Солнца около перигелия в начале января быстрее , чем около афелия в начале июля. Это заставляет процессы, подобные изменению солнечного склонения, происходить в январе быстрее, чем в июле. На графике это делает минимумы более острыми, чем максимумы. Кроме того, поскольку перигелий и афелий не происходят в точные даты солнцестояний, максимумы и минимумы слегка асимметричны. Темпы изменений до и после не совсем равны.
Поэтому график видимого склонения Солнца по-разному отличается от синусоидальной волны. Как показано ниже, его точное вычисление связано с некоторыми трудностями.
Расчеты
Наклонение Солнца , δ ☉ , — это угол между лучами Солнца и плоскостью экватора Земли. Наклон оси Земли ( астрономы называют ее наклоном эклиптики ) — это угол между осью Земли и линией, перпендикулярной орбите Земли. Наклон оси Земли медленно меняется в течение тысяч лет, но его текущее значение ε = 23 ° 26 ‘почти постоянно, поэтому изменение солнечного склонения в течение одного года почти такое же, как и в течение следующего года.
Во время солнцестояний угол между лучами Солнца и плоскостью экватора Земли достигает максимального значения 23 ° 26 ‘. Следовательно, δ ☉ = + 23 ° 26 ‘в день северного летнего солнцестояния и δ ☉ = -23 ° 26′ в период южного летнего солнцестояния.
В момент каждого равноденствия центр Солнца, кажется, проходит через небесный экватор , а δ ☉ равно 0 °.
Склонение Солнца в любой момент рассчитывается по формуле:
δ ⊙ знак равно Arcsin [ грех ( — 23,44 ∘ ) ⋅ грех ( E L ) ] <\ displaystyle \ delta _ <\ odot>= \ arcsin \ left [\ sin \ left (-23,44 ^ <\ circ>\ right) \ cdot \ sin \ left (EL \ right) \ right]>
где EL — долгота эклиптики (по сути, положение Земли на ее орбите). Поскольку эксцентриситет земной орбиты невелик, ее орбиту можно аппроксимировать как круг, что вызывает ошибку до 1 °. Приближение круга означает, что EL будет на 90 ° впереди солнцестояний на орбите Земли (в дни равноденствия), так что sin (EL) можно записать как sin (90 + NDS) = cos (NDS), где NDS — количество дни после декабрьского солнцестояния. Также используя приближение, что arcsin [sin (d) · cos (NDS)] близко к d · cos (NDS), получается следующая часто используемая формула:
δ ⊙ знак равно — 23,44 ∘ ⋅ потому что [ 360 ∘ 365 ⋅ ( N + 10 ) ] <\ displaystyle \ delta _ <\ odot>= — 23,44 ^ <\ circ>\ cdot \ cos \ left [<\ frac <360 ^ <\ circ>> <365>> \ cdot \ left (N + 10 \ right )\верно]>
где N — день года, начинающийся с N = 0 в полночь по всемирному времени (UT), когда начинается 1 января (т.е. часть дней в порядковой дате -1). Число 10 в (N + 10) — это приблизительное количество дней после декабрьского солнцестояния до 1 января. Это уравнение переоценивает склонение около сентябрьского равноденствия до + 1,5 °. Аппроксимация синусоидальной функции сама по себе приводит к ошибке до 0,26 ° и не рекомендуется для использования в приложениях солнечной энергии. Формула Спенсера 1971 года (основанная на ряде Фурье ) также не рекомендуется из-за ошибки до 0,28 °. Дополнительная ошибка до 0,5 ° может возникнуть во всех уравнениях для равноденствий, если не использовать десятичный разряд при выборе N для корректировки времени после полуночи UT для начала этого дня. Таким образом, приведенное выше уравнение может иметь погрешность до 2,0 °, что примерно в четыре раза больше угловой ширины Солнца, в зависимости от того, как оно используется.
Склонение можно более точно рассчитать, если не делать двух приближений, используя параметры орбиты Земли для более точной оценки EL:
δ ⊙ знак равно Arcsin [ грех ( — 23,44 ∘ ) ⋅ потому что ( 360 ∘ 365,24 ( N + 10 ) + 360 ∘ π ⋅ 0,0167 грех ( 360 ∘ 365,24 ( N — 2 ) ) ) ] <\ displaystyle \ delta _ <\ odot>= \ arcsin \ left [\ sin \ left (-23,44 ^ <\ circ>\ right) \ cdot \ cos \ left (<\ frac <360 ^ <\ circ>> < 365,24>> \ left (N + 10 \ right) + <\ frac <360 ^ <\ circ>> <\ pi>> \ cdot 0,0167 \ sin \ left (<\ frac <360 ^ <\ circ>> <365,24 >> \ left (N-2 \ right) \ right) \ right) \ right]>
который можно упростить, оценив константы до:
δ ⊙ знак равно — Arcsin [ 0,39779 потому что ( 0,98565 ∘ ( N + 10 ) + 1,914 ∘ грех ( 0,98565 ∘ ( N — 2 ) ) ) ] <\ displaystyle \ delta _ <\ odot>= — \ arcsin \ left [0,39779 \ cos \ left (0,98565 ^ <\ circ>\ left (N + 10 \ right) +1,914 ^ <\ circ>\ sin \ left ( 0,98565 ^ <\ circ>\ left (N-2 \ right) \ right) \ right) \ right]>
N — количество дней с полуночи UT, когда начинается 1 января (т. Е. Часть дней в порядковой дате -1), и может включать десятичные дроби для корректировки на местное время позже или раньше в течение дня. Число 2 в (N-2) — это приблизительное количество дней до перигелия Земли после 1 января . Число 0,0167 — текущее значение эксцентриситета орбиты Земли. Эксцентриситет очень медленно меняется во времени, но для дат, довольно близких к настоящему, его можно считать постоянным. Наибольшие ошибки в этом уравнении составляют менее ± 0,2 °, но менее ± 0,03 ° для данного года, если число 10 корректируется в большую или меньшую сторону в дробных днях, в зависимости от того, насколько далеко декабрьское солнцестояние предыдущего года произошло до или после. полдень 22 декабря. Эти точности сравниваются с продвинутыми расчетами NOAA, которые основаны на алгоритме Жана Миуса 1999 года с точностью до 0,01 °.
(Приведенная выше формула связана с достаточно простым и точным вычислением уравнения времени , которое описано здесь .)
Более сложные алгоритмы корректируют изменения эклиптической долготы, используя термины в дополнение к поправке на эксцентриситет 1-го порядка, описанной выше. Они также исправляют наклон 23,44 °, который очень незначительно меняется со временем. Поправки также могут включать влияние Луны на смещение положения Земли от центра орбиты пары вокруг Солнца. После определения склонения относительно центра Земли применяется дополнительная поправка на параллакс , которая зависит от расстояния наблюдателя от центра Земли. Эта поправка меньше 0,0025 °. Погрешность вычисления положения центра Солнца может быть менее 0,00015 °. Для сравнения, ширина Солнца около 0,5 °.
Атмосферная рефракция
Вышеописанные расчеты склонения не включают эффекты преломления света в атмосфере, из-за которых видимый угол возвышения Солнца, видимый наблюдателем, оказывается выше фактического угла возвышения, особенно при малых возвышениях Солнца. Например, когда Солнце находится на высоте 10 °, кажется, что оно находится под углом 10,1 °. Наклонение Солнца может использоваться вместе с его прямым восхождением для расчета его азимута, а также его истинного возвышения, которое затем может быть скорректировано на преломление, чтобы определить его видимое положение.
Уравнение времени
В дополнение к ежегодному колебанию видимого положения Солнца с севера на юг, соответствующему описанному выше изменению его склонения, существует также меньшее, но более сложное колебание в направлении восток-запад. Это вызвано наклоном оси Земли, а также изменениями скорости ее орбитального движения вокруг Солнца, вызванными эллиптической формой орбиты. Основными эффектами этого колебания с востока на запад являются изменения во времени таких событий, как восход и закат, а также в чтении солнечных часов по сравнению с часами, показывающими местное среднее время . Как показано на графике, солнечные часы могут быть быстрее или медленнее примерно на 16 минут по сравнению с часами. Поскольку Земля вращается со средней скоростью в один градус каждые четыре минуты относительно Солнца, это 16-минутное смещение соответствует сдвигу на восток или запад примерно на четыре градуса видимого положения Солнца по сравнению с его средним положением. Смещение на запад заставляет солнечные часы опережать время.
Поскольку основной эффект этого колебания касается времени, его называют уравнением времени , используя слово «уравнение» в несколько архаичном смысле, означающем «исправление». Колебания измеряются в единицах времени, минутах и секундах, что соответствует количеству, на которое солнечные часы опережают часы. Уравнение времени может быть положительным или отрицательным.
Аналемма
Аналемма представляет собой диаграмма , которая показывает годовые изменения положения Солнца на небесной сфере , относительно среднего положения, как видно из фиксированного места на Земле. (Слово аналемма также иногда, но редко, используется в других контекстах.) Его можно рассматривать как изображение видимого движения Солнца в течение года , которое напоминает восьмерку. Аналемму можно изобразить, наложив фотографии, сделанные в одно и то же время дня с разницей в несколько дней в течение года .
Аналемму также можно рассматривать как график склонения Солнца , обычно отображаемый вертикально, против уравнения времени , нанесенного горизонтально. Обычно масштабы выбираются так, чтобы равные расстояния на диаграмме представляли равные углы в обоих направлениях на небесной сфере. Таким образом, 4 минуты (точнее 3 минуты 56 секунд) в уравнении времени представлены таким же расстоянием, как 1 ° в склонении , поскольку Земля вращается со средней скоростью 1 ° каждые 4 минуты относительно Солнца. .
Аналемма нарисована так, как если бы наблюдатель смотрел вверх на небе. Если вверху показан север , то справа — запад . Обычно это делается даже тогда, когда аналемма отмечена на географическом глобусе , на котором континенты и т. Д. Показаны с запада влево.
Некоторые аналеммы отмечены, чтобы показать положение Солнца на графике в разные даты с интервалом в несколько дней в течение года. Это позволяет аналемме , которые будут использоваться , чтобы сделать простые аналоговые вычисления величин , такими как время и азимуты от восхода и захода солнца . Аналеммы без даты используются для корректировки времени, показываемого солнечными часами .
Источник