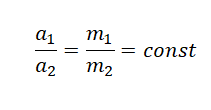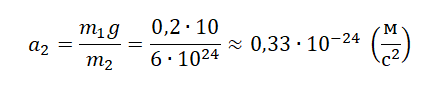Законы Кеплера
Гравитационное взаимодействие проще всего наблюдать на космических объектах, обладающих огромной массой. В окружающей нас повседневности действие гравитации между предметами наблюдать сложно, даже если вес предметов составляет сотни и тысячи килограммов. В микромире силы гравитационного взаимодействия малы настолько, что ими можно пренебречь, потому на первый план выходят другие виды взаимодействий между элементарными частицами и атомами.
Гравитация удерживает живых существ и предметы на поверхности планеты, определяет характер движения планет вокруг Солнца. Именно гравитационное воздействие определяет тот факт, что планеты удерживаются вокруг своих звезд, а спутники не могут уйти в космическое пространство и продолжат движение по орбите вокруг своей планеты.
Закон всемирного тяготения или как его еще называют, теория гравитации, был открыт именно при наблюдении за планетами Солнечной системы.
Если наблюдать за движением небесных тел с Земли, то может показаться, что все эти тела движутся по сложной траектории. Так, например, древний ученый Птолемей, первооткрыватель законов движения планет, поместил Землю в центр вселенной и предположил, что другие планеты и звезды движутся вокруг Земли по большим и малым орбитам.
Рисунок 1 . 24 . 1 . Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд.
Законы движения планет, установленные Птолемеем никем из исследователей не оспаривалась на протяжении 14 веков и только в середине 16 столетия была заменена Коперником на гелиоцентрическую систему, согласно которой все планеты движутся вокруг Солнца.
На основе гелиоцентрической системы объяснить траектории движения небесных тел стало намного проще. На основании трудов Коперника и наблюдений за движением планет астронома из Дании Браге немецкий астроном Кеплер сформулировал три эмпирических закона движения планет в Солнечной системе.
Первый закон Кеплера
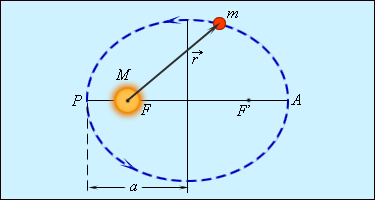
Планеты Солнечной системы движутся по эллиптическим орбитам. В одном из фокусов такой орбиты находится Солнце.
Мы проиллюстрировали первый закон Кеплера рисунком. На нем изображена планета, чья масса меньше массы звезды. Звезда находится в одном из фокусов эллипса, по которому движется планета. Точкой Р мы обозначили ближайшую к звезде траекторию, носящая название перигелия. Точка А – это наиболее удаленная от звезды точка траектории, которая называется афелием. Большая ось эллипса располагается между точками афелии и перигелия.
Рисунок 1 . 24 . 2 . Эллиптическая орбита планеты массой m M . a – длина большой полуоси, F и F ‘ – фокусы орбиты.
В Солнечной системе все планеты за исключением Плутона движутся по орбитам, которые близки к круговым.
Второй закон Кеплера, или закон площадей
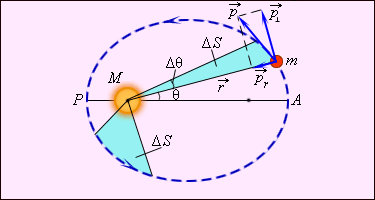
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Рисунок 1 . 24 . 3 . Закон площадей – второй закон Кеплера.
Эквивалентом второго закона Кеплера можно считать закон сохранения момента импульса. На рисунке, расположенном выше, изображен вектор импульса тела p → и составляющие его p r → и p ⊥ → . Площадь, заметенная радиус-вектором за малое время Δ t , приближенно равна площади треугольника с основанием r Δ θ и высотой r :
∆ S = 1 2 r 2 ∆ θ или ∆ S ∆ t = 1 2 r 2 ∆ θ ∆ t = 1 2 r 2 ω ; ( ∆ t → 0 ) .
Здесь ω = ∆ θ ∆ t ; ( ∆ t → 0 ) – угловая скорость.
Момент импульса L по абсолютной величине равен произведению модулей векторов p r → и p ⊥ → :
L = r p ⊥ = r ( m v ⊥ ) = m r 2 ω так как v ⊥ = r ω .
Из этих отношений следует:
∆ S ∆ t = L 2 m , ∆ t → 0
Поэтому, если по второму закону Кеплера ∆ S ∆ t = co n s t , то и момент импульса L при движении остается неизменным.
В частности, поскольку скорости планеты в перигелии v P → и афелии v A → направлены перпендикулярно радиус-векторам r P → и r A → из закона сохранения момента импульса следует:
r P v p = r A u A
Третий закон Кеплера
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.
Формула третьего закона Кеплера имеет вид:
T 2 a 3 = c o n s t или T 1 2 a 1 3 = T 2 2 a 2 3
Точность, с которой третий закон Кеплера выполняется для всех планет, составляющих Солнечную систему, составляет выше 1 % .
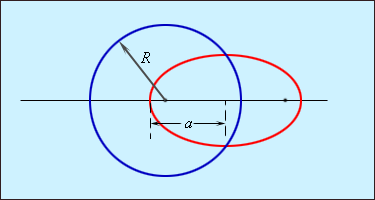
На рисунке изображены две орбиты, по которым небесные тела движутся вокруг звезды. Одна из орбит круговая с радиусом R , а другая – эллиптическая с большой полуосью a . Если R = a , то согласно третьему закону Кеплера периоды обращения планет по таким орбитам будут одинаковы.
Рисунок 1 . 24 . 4 . Круговая и эллиптическая орбиты. При R = a периоды обращения тел по этим орбитам одинаковы.
Рисунок 1 . 24 . 5 . Модель законов Кеплера.
Законы Кеплера очень долго были правилами, полученными эмпирически на основе наблюдений за движением небесных тел. Для того, чтобы получить возможность опираться на них в создании рабочих теорий, не хватало теоретического обоснования законов.
Таким обоснованием стало открытие закона всемирного тяготения Исааком Ньютоном:
Закон всемирного тяготения:
где M и m – массы Солнца и планеты, r – расстояние между ними, G = 6 , 67 · 10 – 11 Н · м 2 / к г 2 – гравитационная постоянная.
Ньютон был первым из исследователей, кто пришел к выводу о том, что между любыми телами в космосе действуют гравитационные силы, которые и определяют характер движения этих тел. Частным случаем такого взаимодействия является сила тяжести, воздействующая на тела, расположенные на поверхности и вблизи планет.
Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2
R 3 , где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:
ω 2 R = 2 π 2 R T 2 .
Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.
Потенциальная энергия тела массы m , находящегося на расстоянии r от неподвижного тела массы M , равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность.
Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях.
Рисунок 1 . 24 . 6 . Вычисление потенциальной энергии тела в гравитационном поле.
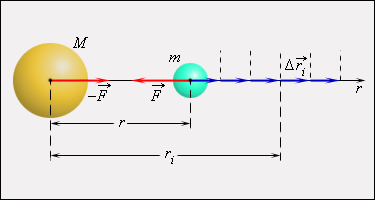
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа ∆ A i гравитационной силы F → на малом перемещении ∆ s i → = ∆ r i → есть:
∆ A i = — G M m r i 2 ∆ r i
Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ Δ A i на малых перемещениях:
В пределе при Δ r i → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение:
E p = A r ∞ = — G M m r
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.
Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость v , его полная механическая энергия равна
E = E k + E p = m v 2 2 — G M m r = c o n s t
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
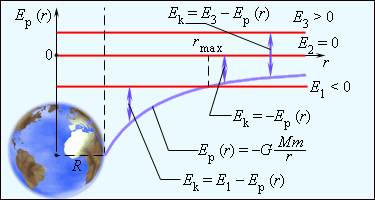
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1 . 24 . 6 ).
При E = E 1 0 тело не может удалиться от центра притяжения на расстояние r > r m a x . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).
Рисунок 1 . 24 . 7 . Диаграмма энергий тела массой m в гравитационном поле, создаваемом сферически симметричным телом массой M и радиусом R .
При E = E 2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории.
При E = E 3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.
Первая и вторая космические скорости
Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.
Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.
m v 1 2 R 3 = G M m R 3 2 = g m , отсюда v 1 = G M R 3 = g R 3 = 7 , 9 · 10 3 м / с .
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
E = m v 2 2 2 — G M m R 3 = 0 , отсюда v 2 = 2 G M R 3 = 2 g R 3 = 11 , 2 · 10 3 м / с .
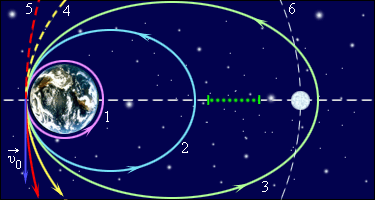
Мы проиллюстрировали понятие первой и второй космической скорости рисунком. Если скорость космического корабля равна v 1 = 7 . 9 · 10 3 м / с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих v 1 , но меньших υ 2 = 11 , 2 · 10 3 м / с , орбита корабля будет эллиптической. При начальной скорости v 2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.
Рисунок 1 . 24 . 8 . Космические скорости. Указаны скорости вблизи поверхности Земли. 1 : v = v 1 – круговая траектория; 2 : v 1 v v 2 – эллиптическая траектория; 3 : v = 11 , 1 · 10 3 м / с – сильно вытянутый эллипс; 4 : v = v 2 – параболическая траектория; 5 : v > v 2 – гиперболическая траектория; 6 : траектория Луны.
Источник
Законы Ньютона. Динамика.
теория по физике 🧲 динамика
Три закона Ньютона
Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.
Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.
Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.
Основное утверждение механики
Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:
Основное утверждение механики
Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.
Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).
Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.
Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.
Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон Ньютона
Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.
Первый закон Ньютона
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.
Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.
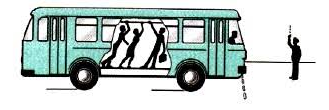
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.
Второй закон Ньютона
В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.
Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).
Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.
Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.
Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.
Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.
Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.
Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.
Второй закон Ньютона
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела
Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сила — векторная физическая величина. Обозначается F . Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.
Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с 2 . Масса яблока равна 200 г.
Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:
F = ma = 0,2 ∙ 9,8 = 1,96 (Н)
Равнодействующая сила
Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.
Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.
В этом случае второй закон Ньютона формулируется так:
Второй закон Ньютона через равнодействующие силы
Если на тело действует несколько сил, но их равнодействующая R будет равна произведению массы на ускорение этого тела.
Правила сложения сил и их проекций
Сложение двух сил, направленных вдоль одной прямой в одну сторону
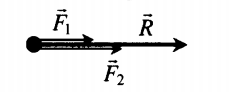
Если F 1↑↑ F 2, то: Равнодействующая сила сонаправлена с обеими силами.
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях
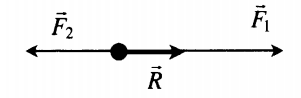
Если F 1↑↓ F 2, то: Равнодействующая сила направлена в сторону направления большей по модулю силы.
Сложение двух сил, перпендикулярных друг к другу
Если F 1 перпендикулярна F 2, то равнодействующая сила вычисляется по теореме Пифагора: 
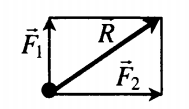
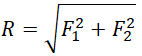
Сложение двух сил, расположенных под углом α друг к другу
Если F 1 и F 2 расположены под углом α друг к другу, равнодействующая сила вычисляется по теореме косинусов: 
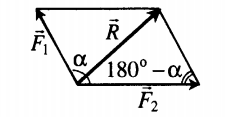
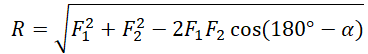
Сложение трех сил
Способ сложения определяется правилами сложения векторов. В данном случае: 
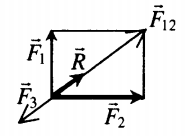
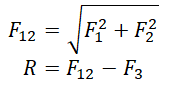
Сложение проекций сил
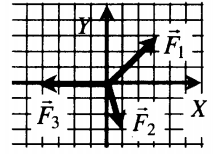
Проекция на ось ОХ: Проекция на ось OY:
Третий закон Ньютона
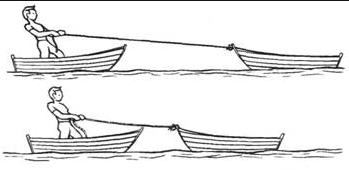
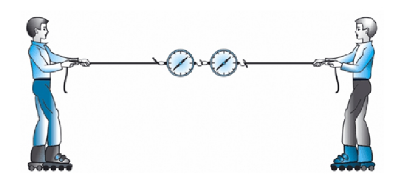
Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.
Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.
Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.
Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
Используя второй закон Ньютона, третий закон механики можно переписать иначе:
Отношение модулей ускорений a 1 и a 2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.
Пример №2. Определить ускорение, с которым движется Земля к падающему на нее яблоку. Масса яблока равна 0,2 кг. Ускорение свободного падения принять равной за 10 м/с 2 . Массу Земли принять равно 6∙10 24 кг.
Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:
Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a1 будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:
Скорость тела массой 5 кг, движущегося вдоль оси Ох в инерциальной системе отсчёта, изменяется со временем в соответствии с графиком (см. рисунок). Равнодействующая приложенных к телу сил в момент времени t=2,5 с равна…
Источник