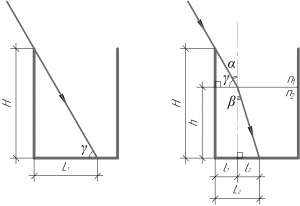
Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько
Условие задачи:
Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько изменится длина тени на дне сосуда при освещении его солнечными лучами, если в сосуд налить воду до высоты 20 см?
Задача №10.3.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
\(\gamma=60^\circ\), \(H=25\) см, \(h=20\) см, \(\Delta L-?\)
Решение задачи:
Если посмотреть на рисунок к задаче, то видно, что длину тени \(L_1\) в пустом сосуде можно найти по формуле:
Далее сосуд наполняют водой. Из-за того, что луч при переходе из воздуха в воду претерпевает преломление, то длина тени теперь будет короче (см. рисунок к задаче). При этом длину тени на дне сосуда можно определить как сумму:
При этом из прямоугольных треугольников можно найти длины \(l_1\) и \(l_2\) по следующим формулам:
То есть формула (1) примет вид:
\[
Запишем закон преломления света (также известен как закон преломления Снеллиуса):
Здесь \(\alpha\) и \(\beta\) – угол падения и угол преломления соответственно, \(n_1\) и \(n_2\) – показатели преломления сред. Показатель преломления воздуха \(n_1\) равен 1, показатель преломления воды \(n_2\) равен 1,33.
Так как из рисунка хорошо видно, что \(\alpha = 90^\circ – \gamma\), то:
Поскольку \(\sin \left( <90^\circ – \gamma >\right) = \cos \gamma\), имеем:
Полученное выражение подставим в формулу (2), тогда:
Очевидно, что изменение длины тени следует искать по формуле:
Учитывая выражения (1) и (3), имеем:
\[\Delta L = H \cdot ctg\gamma – \left(
\[\Delta L = h \cdot ctg\gamma – h \cdot tg\left( <\arcsin \left( <\frac<<
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
\[\Delta L = 0,2 \cdot ctg60^\circ – 0,2 \cdot tg\left( <\arcsin \left( <\frac<<1 \cdot \cos 60^\circ >><<1,33>>> \right)> \right) = 0,0343\;м = 3,43\;см\]
Ответ: 3,43 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник