Вычислите среднюю плотность солнца сравните ее со средней плотностью земли

В общем случае сказать трудно — это зависит от задачи и от того, насколько сильно Вы «немного ошиблись» в вычислениях. Как правило, если задача достаточно сложная, то просто арифметическая ошибка означает снижение результата с 8 баллов (даваемых за полное решение) до 7.

Однако возможны варианты, когда баллов будет меньше:
1) Полученный ответ является очевидно нелепым. Например, если в 5-й задаче этой параллели при вычислении гравитационного радиуса ошибиться на порядок, то это сойдет за арифметическую ошибку. Но если участник получил (из-за ошибки при подсчете) величину гравитационного радиуса, заметно превышающую размеры типичной галактики, то это ему обойдется дороже.
2) Вычисления являются существенной частью задачи. На районном туре такое встречается редко, но вообще бывают задачи, где идея решения тривиальна, а сложность состоит в придумывании алгоритма вычисления результата с нужной точностью при приемлимых затратах времени.

Нестандартный путь — это хорошо. Нередко нестандартные решения оцениваются даже «дороже», чем стандартные (9 или 10 баллов вместо обычных 8 ). Другое дело, что «нестандартное решение» может на самом деле оказаться некорректным, обеспечивающим совпадение результата с правильным только вследствие некоторой случайности. Тогда, конечно, баллов будет меньше: 1-2 за «попадание» в ответ (если оно было) и еще 1-3 за более или менее разумные детали, если они были в решении.

Источник

Определите среднюю плотность Солнца, если период обращения Земли вокруг Солнца принять равным 365 сут. При расчётах принять радиус земной орбиты равным 150 млн км, а радиус Солнца — 700 тыс. км.

Напишите с Дано пж CРООООЧНО

радиус солнца: 7*10^8 м,

объем солнца: 4/3*pi*R^3 = 1.44*10^27 м3

земля летит со скоростью: v = (2*pi * 150млн км) /(365суток) = (2*pi*1.5*10^11 м) /(365*86400 сек) = 3*10^4 м/с

v^2/r = a (центростремительное ускорение) = G*M/r^2

масса солнца M = v^2*r/G = (3*10^4 м/с) ^2*(1.5*10^11 м) /(6.7*10^-11) = 2.0*10^30 кг

плотность = M/объем = (2.0*10^30 кг) /(1.44*10^27 м3) = 1400 кг/м3

Если ответ по предмету Математика отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.

Чтобы отыскать на небе светило, надо указать в какой стороне горизонта и как высоко оно находится.

Для этого используется горизонтальная система координат: азимут и высота. Наблюдатель на Земле должен определить вертикальное и горизонтальное направления.

Вертикальное направление определяется с помощью отвеса (на чертеже — линия ZZ’)

Высота сердце светила отсчитывается по окружности, проходящей через зенит и светило, и выражается длиной дуги этой окружности.от горизонта.

Азимут (A) — положение светила относительно сторон горизонта, отсчитывается от точки юга в направлении движения часовой стрелки.

Источник

Вычислите среднюю плотность солнца сравните ее со средней плотностью земли

Источник

Как измерить массу Земли и массу Солнца?

Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

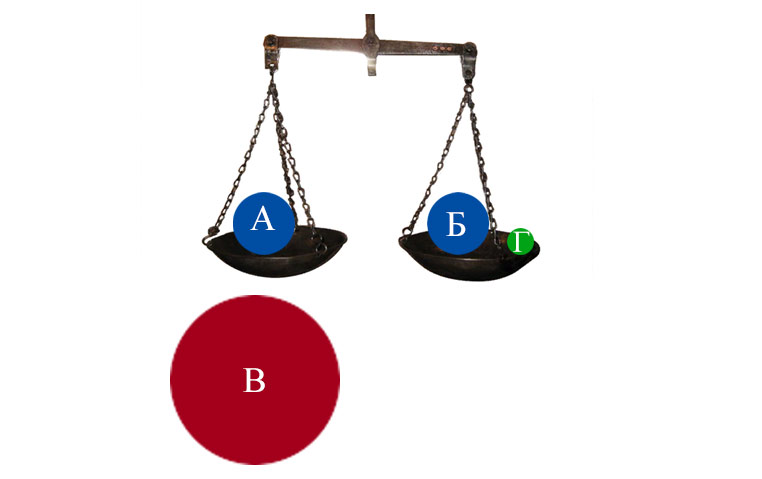
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

Как вычислить массу планеты Земля, не выходя из дома?

Вас может заинтересовать

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.

А теперь измерим массу Солнца!

Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

Источник

О массах и плотностях планет

То, что планеты Солнечной системы значительно различаются по своему размеру, является хорошо известным фактом.

Так, например, планеты внутренней части нашей системы имеют меньшие размеры, но являются более плотными, чем газовые или ледяные гиганты, располагающиеся во внешней части Солнечной системы. А в ряде случаев, планеты могут быть даже меньше, чем некоторые спутники. Однако размер планеты не обязательно пропорционален его массе.

Таким образом, в то время как Меркурий может быть меньше по размеру, чем спутник Юпитера Ганимед или спутник Сатурна Титан, он более чем в два раза массивнее этих спутников. И в то время как Юпитер в 318 раз массивнее Земли, его радиус лишь в 11,21 раза больше земного.

Давайте пройдёмся по каждой из планет и посмотрим, насколько они различаются.

Меркурий

Со средним диаметром 4879 километров (3031,67 миль) Меркурий является самой маленькой планетой Солнечной системы. Он также является второй (после Земли) по плотности планетой: 5,427 г/см 3 .

Меркурий, как и другие планеты земной группы состоит из силикатных пород и минералов, а также железного ядра, которое в отличии от других планет является аномально большим по отношению к коре и мантии. Таким образом масса Меркурия составляет около 0,330*10 24 кг., что эквивалентно 0,055 массы Земли. Сила меркурианского притяжения составляет всего 3,7 м/с 2 .

Венера

Венера, которая из-за сходства состава, размера и массы порой часто именуется “сестрой Земли” имеет плотность 5,243 г/см 3 . Она является второй планетой от Солнца, а её средний радиус составляет примерно 6050 километров (3759,3 миль). Таким образом масса планеты достигает 4,87*10 24 кг., что эквивалентно 0,815 массы Земли. Учитывая плотность и размеры, сила тяжести на Венере сопоставима с Земной и равна примерно 8,87 м/с 2 .

Земля

Как и другие планеты внутренней части Солнечной системы, Земля также состоит из металлов и силикатов. Со средним радиусом 6371 километров (3 958 миль) и средней плотностью 5,514 г/м 3 , она является наиболее крупной и самой плотной, из планет земной группы. Масса Земли достигает 5,97*10 24 кг., а сила земного притяжения, как все вы знаете равна 9,8 м/с 2 .

Марс является третьей по величине планетой земной группы. Как и другие, Марс состоит из металлов и силикатных пород, но в то время как он примерно в два раза меньше Земли (со средним диаметром 6792 километров, или 4220 миль), его масса составляет всего одну десятую массы Земли.

Короче говоря, Марс имеет массу 0,642*10 24 кг., или примерно 0,11 массы Земли. Учитывая размеры и плотность (составляющую 3,9335 г/см 3 ) сила притяжения на Марсе не превышает 3,8 м/с 2 .

Юпитер

Юпитер является самой крупной планетой в Солнечной системе. Учитывая то, что его средний диаметр равен 142984 километров, в нём могут поместиться все другие планеты нашей системы (кроме Сатурна). Однако с массой 1898*10 24 кг., Юпитер почти в 2,5 раза массивнее всех других планет в Солнечной системе вместе взятых. Тем не менее, как газовый гигант, он имеет более низкую общую плотность, чем планеты земной группы. Его средняя плотность равна 1,326 г/см 3 .

Сатурн

Сатурн является вторым по величине газовым гигантом; и со средним диаметром 120536 километров, он всего лишь немного меньше, чем Юпитер. Тем не менее, он значительно менее массивен, чем его двоюродный брат Юпитер. С массой 569*10 24 кг. Сатурн в 95 раз массивнее Земли, однако его плотность составляет всего 0,687 г/см 3 . Сатурн является единственной планетой в Солнечной системе, которая имеет меньшую плотность, чем вода (1 г/см 3 ).

Средний диаметр Урана равен 120536 километров, он является третьей по величине планетой в Солнечной системе. С массой 86,8*10 24 кг., Уран – это четвёртая наиболее массивная планета. Средняя плотность, таким образом, достигает 1,271 г/см 3 .

Нептун

Нептун примерно в четыре раза больше Земли (диаметр 49528 километров), а его масса равна 102*10 24 кг. Таким образом плотность Нептуна больше, чем плотность любого из газовых гигантов (1,638 г/см 3 ).

Исходя из вышесказанного, вы можете увидеть, что массы планет Солнечной системы значительно варьируются. Но если мы говорим о плотности, то она не всегда пропорциональна размерам. Короче говоря, в то время как некоторые планеты могут быть всего в несколько раз больше, чем другие, они при этом могут быть во много и много раз более массивными.

Источник