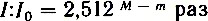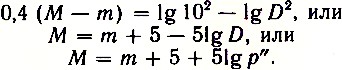Видимая звездная величина солнца по отношению абсолютной звездной величине

Фотометрия космических объектов является частью астрофизики. Однако фотометрия, особенно звёздная, играет огромную роль в звёздной астрономии, поэтому необходимо ознакомиться с основными понятиями фотометрии.

Видимая звёздная величина m является мерой освещенности E, создаваемой источником на перпендикулярной к его лучам поверхности в месте наблюдения с учетом поглощения света атмосферой Земли. Связь между звёздной величиной m и освещенностью E есть отражение установленного экспериментально психофизиологического закона Вебера-Фехнера и выражается формулой:

в которой коэффициент введен в середине XIX в. английским астрономом Н. Погсоном, подметившим, что в среднем у наблюдателей интервалу в 5 звёздных величин соответствует отношение световых потоков или освещенностей около 100. Погсон принял это отношение в точности равным 100, при этом

В итоге ослабление блеска на одну звёздную величину соответствует ослаблению освещенности от объекта лишь немногим более чем в 2.5 раза. Величина a представляет собой нуль-пункт шкалы звёздных величин, связанный с выбором фотометрического стандарта. В качестве стандарта обычно выбирается та или иная группа звёзд с точно измеренным блеском. По отношению к звёзде стандарта можно определить блеск любой звезды по формуле:

где нулевым индексом обозначена соответствующая величина для звезды-стандарта.

Для звезды с известной видимой звёздной величиной и известным расстоянием от Солнца можно вычислить абсолютную звёздную величину , которая является мерой ее светимости — количества энергии, излучаемой звёздой во всех направлениях. Абсолютная звёздная величина определяется как видимая величина звезды, перенесенной на стандартное, общее для всех звёзд расстояние. Зная видимую звёздную величину V (с этого момента мы для определенности будем обозначать звёздные величины так, как это принято в фотометрической системе UBV) и расстояние до объекта, можно легко определить абсолютную величину M_V, помня, что изменению расстояния до объекта в отношении r/r₀ соответствует изменение освещенности в отношении (r/r₀)2. Следовательно,

и логарифмирование этого выражения показывает, что абсолютная величина M_V определяется по формуле:

Расстояние r₀ удобно принять равным 10 парсекам. Таким образом, если расстояние до звезды выражено в парсеках, то имеем:

Последнее выражение справедливо только в том случае, если между наблюдателем и звёздой нет рассеивающей (поглощающей) свет материи. Если такая материя имеется, то часть разницы (V — M_V) следует отнести за счёт рассеяния или поглощения света этой материей. При этом поглощение света влияет только на видимую звёздную величину V, не меняя M_V, так как абсолютная звёздная величина является характеристикой самой звезды. Поглощение света уменьшает блеск звезды, поэтому увеличивает значение видимой звёздной величины, и в выражение (2-6) следует ввести член, учитывающий поглощение света A_V, которое является, в общем случае, функцией расстояния от наблюдателя и направления на звёзду:

Величина V — M_V носит название модуль расстояния , при этом, если мы не учитываем поглощение света, то модуль расстояния называется видимым, а если поглощение света учтено, то истинным, обозначаемым (V₀ — M_V). Естественно, мы должны всегда стремиться получить из наблюдательных данных истинный модуль расстояния, так как только эта величина дает возможность оценить истинное расстояние до космического объекта. Определение абсолютных звёздных величин (а, значит, и светимостей) звёзд и модулей расстояния (а, значит, и самих расстояний) является важнейшей задачей звёздной астрономии.

Отметим, что мы ставим в обозначении абсолютной звёздной величины индекс V для того, чтобы подчеркнуть, что M_V есть мера энергии, излучаемой звёздой в определенном спектральном интервале, а не во всех областях спектра.

Источник

Чему равна звездная величина нашего Солнца?

Наиболее яркие звезды без труда видны на засвеченном городском небе, а самые тусклые едва различимы при идеальных условиях наблюдения. Для характеристики блеска звезд и других небесных светил (например, планет, метеоров, Солнца и Луны) ученые разработали шкалу звездных величин.

Наиболее яркие звезды условились называть звездами 1-й звездной величины; те из звезд, которые по своему блеску в 2,5 раза (точнее, в 2,512 раза) слабее звезд 1-й величины, получили наименование звезд 2-й звездной величины. К звездам 3-й звездной величины отнесли те из них. которые слабее звезд 2-й величины в 2,5 раза, и т. д. Самые слабые из звезд, доступных невооруженному глазу, были причислены к звездам 6-й звездной величины . Нужно помнить, что название «звездная величина» указывает не на размеры звезд, а только на их видимый блеск.

В 1856 году Норман Погсон предложил следующую формализацию шкалы звёздных величин, ставшую общепринятой:

где m — звёздные величины объектов, L — освещённости от объектов. Такое определение соответствует падению светового потока в 100 раз при увеличении звёздной величины на 5 единиц.

Следующие свойства помогают пользоваться видимыми звёздными величинами на практике:

Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц.
Уменьшение звёздной величины на одну единицу означает увеличение светового потока.

Данная формула даёт возможность определить только разницу звёздных величин, но не сами величины.

Видимые звездные величины некоторых небесных тел

Солнце: -26,73
Луна (в полнолуние): -12,74
Венера (в максимуме блеска): -4,67
Юпитер (в максимуме блеска): -2,91
Сириус: -1,44
Вега: 0,03
Самые слабые звезды, видимые невооруженным глазом: около 6,0
Солнце с расстояния 100 световых лет: 7,30
Проксима Центавра: 11,05
Самый яркий квазар: 12,9
Самые слабые объекты, снимки которых получены телескопом «Хаббл»: 31,5

Источник

Видимая и абсолютная звёздные величины. Светимость звёзд

Светимостью называется полная энергия, излучаемая звездой в единицу времени.

Она выражается в абсолютных единицах (ваттах) или в единицах светимости Солнца.

В астрономии принято сравнивать звёзды по светимости, рассчитывая их блеск (звёздную величину) для одного и того же стандартного расстояния — 10 пк.

Видимая звёздная величина, которую имела бы звезда, если бы находилась от нас на расстоянии D₀ =10 пк, получила название абсолютной звёздной величины М.

Рассмотрим, как можно определить абсолютную звёздную величину М, зная расстояние до звезды D (или параллакс — р) и её видимую звёздную величину m. Напомним, что блеск двух источников, звёздные величины которых отличаются на единицу, отличается в 2,512 раза. Для звёзд, звёздные величины которых равны m₁, и m₂ соответственно, отношение их блесков I₁, и I₂ выражается соотношением:

I₁, : I₂ = 2,512 m₂ — m₁ .

Для видимои и абсолютной звездных величин одной и той же звезды отношение блесков будет выглядеть так:

I : I₀ = 2,512 М — m ,

где I₀ — блеск этой звезды, если бы она находилась на расстоянии D₀ = 10 пк. В то же время известно, что блеск звезды меняется обратно пропорционально квадрату расстояния до неё. Поэтому

Следовательно,

Логарифмируя это выражение, находим

0,4(M — m) = lg 10 2 — lg D 2 ,

или

М = m + 5 — 5 lg D,

или

М = m + 5 + lg p.

Абсолютная звёздная величина Солнца Иначе говоря, с расстояния 10 пк наше Солнце выглядело бы как звезда пятой звёздной величины. Зная абсолютную звёздную величину звезды М, легко вычислить её светимость L. Считая светимость Солнца получаем:

L = 2,512 5 — M ,

или

lg L = 0,4(5 — M).

По светимости (мощности излучения) звёзды значительно отличаются друг от друга: некоторые излучают энергию в сотни тысяч раз больше, чем Солнце, другие — в десятки тысяч раз меньше. Абсолютные звездные величины звезд наиболее высокой светимости (гигантов и сверхгигантов) достигают М = -9 m , а звёзды-карлики, обладающие наименьшей светимостью, имеют абсолютную звездную величину М = +17 m .

Источник

§22.3. Видимая и абсолютная звездная величина. Светимость звезд

Вспомним, что разность в 5 видимых звездных величин соответствует различию яркости ровно в 100 раз (см. § 3.2). Следовательно, разность видимых звездных величин двух источников равна единице, когда один из них ярче другого ровно в раз (эта величина примерно равна 2,512). Чем ярче источник, тем его видимая звездная величина считается меньшей. В общем случае отношение видимой яркости двух любых звезд I₁:I₂ связано с разностью их видимых звездных величин m₁ и m₂ простым соотношением:

Абсолютной звездной величиной М называется та видимая звездная величина, которую имела бы звезда, если бы находилась от нас на стандартном расстоянии D₀ = 10 пк.

Светимостью звезды L называется мощность излучения световой энергии по сравнению с мощностью излучения света Солнцем.

Величины L и М легко вычислить, если известно расстояние до звезды D или ее параллакс р (так как D обратно пропорционально р) Пусть m — видимая звездная величина звезды, находящейся на расстоянии D. Если бы она наблюдалась с расстояния D₀ = 10 пк, ее видимая звездная величина m0 по определению была бы равна абсолютной звездной величине М. Тогда ее кажущаяся яркость изменилась бы в

Кажущаяся яркость звезды меняется обратно пропорционально квадрату расстояния до нее. Поэтому

Эти формулы дают абсолютную звездную величину М по известной видимой звездной величине m при реальном расстоянии до звезды D. Наше Солнце с расстояния 10 пк выглядело бы примерно как звезда 5-й видимой звездной величины, т. е. для Солнца М = Mc = 5.

Зная абсолютную звездную величину М какой-нибудь звезды, можно вычислить ее светимость L. По определению

Величины М и L в разных единицах выражают мощность излучения звезды независимо от расстояния до нее.

Абсолютные величины очень ярких звезд отрицательны и доходят до М = — 9. Такие звезды называются гигантами и сверхгигантами Звезда S Золотой Рыбы ярче нашего Солнца в 500 000 раз, ее светимость L = 500 000, но видно ее в южном полушарии неба лишь в сильный бинокль. А наше Солнце считается звездой-карликом! Наименьшую мощность излучения имеют красные карлики с М = + 17 и L = 0,000013.

Существуют звезды одинаковой температуры и цвета, но с разной светимостью. У таких звезд спектры в общем одинаковы, однако можно заметить различия в относительных интенсивностях некоторых линий. Это происходит от того, что при одинаковой температуре давление в их атмосферах несколько различно. В атмосферах звезд-гигантов давление меньше, они разреженнее. Если для подобных звезд построить график, показывающий, как меняется отношение интенсивности определенных пар спектральных линий в зависимости от абсолютной величины звезд, то мы сможем по интенсивности линий из графика найти абсолютную величину М звезды. Подстановка найденного значения М в выведенную нами формулу (4) дает возможность определить расстояние до звезды.

Источник

Звёздные величины и как их определяют

На самом деле, звёздные величины могут быть разными. Так как нет идентичных тел в нашей Вселенной. Конечно, существуют схожие черты и параметры, по которым мы объединяем какие-либо объекты. Но всегда есть хоть малейшее различие между ними.
В астрономии понятие звёздная величина обозначает безразмерную (то есть имеет размерность единица) числовую характеристику яркости объекта. Таким образом, она отражает поток энергии всех фотонов за секунду времени на единицу площади, исходящих от светила.

Фотон (частица света)

Какие бывают звёздные величины

Что интересно, в астрономии различают две звёздные величины: видимую и абсолютную.

Видимая звёздная величина

Она отражает видимый блеск звёзд и используется для визуальных величин (измеряются в ультрафиолетовом, инфракрасном и других диапазонах).
Собственно говоря, данная мера зависит от светимости и расстояния до тела.
Что интересно, чем меньше видимый показатель светила, тем, на самом деле, больше его яркость.

Сириус (самая яркая звезда)

Абсолютная звёздная величина

А вот её применяют для наиболее точной характеристики объекта, которая равна значению при расстоянии от него 10 парсек. Для сравнения светимости звёзд используют именно абсолютную величину, так как для этого неважно насколько они удалены от нас.
Более того, чтобы вычислить светимость, необходимо знать абсолютное значение яркости звезды.

Как определяется звёздная величина

Впервые, еще во 2 веке до нашей эры, астроном из Древней Греции Гиппарх разделил звёзды по величине. Он выделил ярчайшие из них, присвоив им первую, а самым тусклым светилам шестую величину.
Проще говоря, звезда первой звездной величины это самая яркая на небе.
Действительно, первым ввёл такую характеристику Гиппарх. Но со временем многие другие учёные изучали космические тела и пополняли данные о них.
Так, позднее в 1856 году Норман Погсон предложил иное исчисление шкалы значений светил. И она стала общепринятой.

Формула Погсона

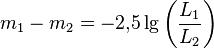
где m — звёздная величина тела, а L — освещённость от него.
Стоит отметить, что по формуле Погсона можно рассчитать лишь разницу между величинами, но не их. Поскольку для вычисления необходим нулевой пункт (блеск, соответствующий нулевой мере звезды).
Раньше нуль-пункт был равен блеску Веги, но со временем его переопределили. Хотя при визуальном наблюдении Вегу всё так же принимают за нулевую меру.

Как оказалось, ярчайшие объекты имеют отрицательную звёздную величину.

картинка название-шкала звездных величин

Шкала звёздных величин

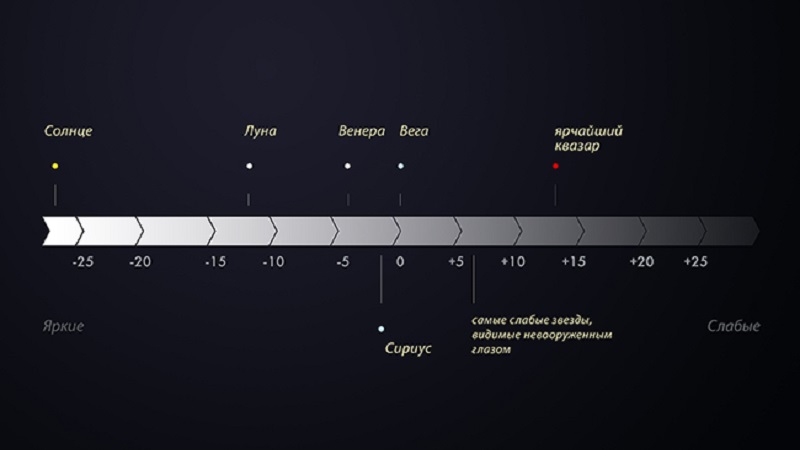
Между прочим, в современной астрономии звездные величины применяют не только для светил, а также для планет и других небесных тел. Но при их характеристике учитывают и видимое, и абсолютное значение.

Итак, яркость звезд и звездная величина являются важным показателем объекта. Разумеется, они зависят от других химических и физических свойств тела.
Конечно, свет светил ярко выделяется на ночном небе. Однако современные приборы и техника позволяют астрономам разглядеть звезды с высокой величиной. Проще говоря, стало возможным увидеть даже самые тусклые светила.

Источник