Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
Условие задачи:
Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца в 108 раз больше радиуса Земли, а плотность в 4 раза меньше плотности Земли? (\(g=9,8\) м/с 2 )
Задача №2.5.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
\(R_с=108R_з\), \(\rho_с=0,25\rho_з\), \(g_з=9,8\) м/с 2 , \(g_с-?\)
Решение задачи:
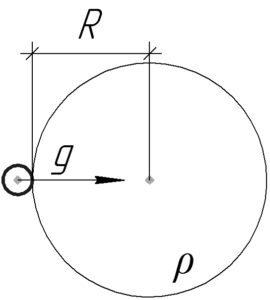
Массу планеты можно найти из её средней плотности \(\rho\) и объема \(V\):
Планеты обычно имеют форму, близкую к шарообразной, поэтому объем \(V\) можно посчитать по следующей формуле:
Подставим выражения (2) и (3) в формулу (1), тогда:
Видно, что ускорение свободного падения вблизи поверхности некоторой планеты зависит линейно от средней плотности и радиуса планеты. Учитывая это, ускорения свободного падения на Земли и на Солнце можно определить по следующим формулам:
\[\left\< \begin
g_c = \frac<4><3>G\pi \rho_с R_с \hfill \\
g_з = \frac<4><3>G\pi \rho_з R_з \hfill \\
\end
Разделим верхнее равенство на нижнее:
Так как в условии сказано, что \(R_с=108R_з\) и \(\rho_с=0,25\rho_з\), то:
Осталось посчитать численный ответ:
\[g = 27 \cdot 9,8 = 264,6\; м/с^2\]
Ответ: 264,6 м/с 2 .
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Источник
Каким стало бы ускорение свободного падения на поверхности Солнца?
Ускорение свободного падения зависит как от массы так и от радиуса небесного тела. g=GM/R^2, для солнца g=6,672*10^(-11)*1.989*10^30/48,4402*10^16=273,8м/с^2. масса Солнца в 333 000 раза больше массы Земли. 9,8*333 000=326340м/с^2. Ускорение свободного падения на Солнце 273.8 м/с^2
1 9 · Хороший ответ
4 9 · Хороший ответ
«Обожаю» анонимные вопросы по физике. Интересно, кто их задаёт.
Вспоминается анекдот, когда на Солнце отправили космонавтов, а чтобы они не сгорели — отправились туда ночью. Примерно такой же уровень) А вообще, домашнее задание лучше выполнять самому.
1 0 · Хороший ответ
Наскольку я помню — лень пересчитывать — на уровне фотосферы Солнца (его видимой » поверхности») ускорение свободного ппдения составляет 28 g, то есть около 280 м/сек^2. Вторая космическая — 617 км/сек.
8 · Хороший ответ
вот загнул! вторая космич скорость-8 с чем-то км в сек!
1 · Хороший ответ
Ну да. Если бы не испарились бы,только лишь косувшись солнечной фотосферы
Смотря что понимать под термином «поверхность Солнца». Если то место где его нет не в коей мере, то это место где-то за пределами орбиты Плутона.
3 · Хороший ответ
кстати, кто не знает — центр масс Солнечной системы не в центре Солнца.
так что у Солнца тоже есть своя «орбита».
Солнце вообще-то «слоёное», часть энергии черпает из Гравитационного сжатия — до открытия термоядерных реакций (теоретического) так и считали — мол Солнце большое, само себя сжимает и при этом греется до температуры 6000 К.
Источник
 Задачи с решениями
Задачи с решениями 

Определите ускорение силы тяжести на Солнце по следующим данным: расстояние от Земли до Солнца , угол, под которым Солнце видно с Земли, , период обращения Земли вокруг Солнца .
Ускорение силы тяжести на Солнце найдем, применив совместно закон всемирного тяготения и второй закон Ньютона для тела массой , находящегося вблизи поверхности Солнца:
Здесь – гравитационная постоянная, – масса Солнца, – радиус Солнца. Радиус Солнца определяется из геометрических соображений (рис. 1.10.1).
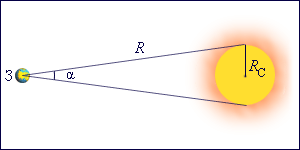 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рисунок 1.10.1. Массу Солнца можно определить, применив второй закон Ньютона к орбитальному движению Земли: Подставляя выражения для и в формулу для ускорения свободного падения , получим: Источник Ускорение свободного паденияУскорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с². На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы. Таблица ускорения свободного падения небесных тел
От чего зависит ускорение свободного падения?Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение). Возможно для будущих вычислений нужны будут эти данные:
Как найти ускорение свободного падения?Формула ускорения свободного паденияГравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле: Пример расчёта ускорения свободного падения (для Земли): Как узнать время падения тела?Формула времени свободного падения (когда тело падает вертикально):
Нужно найти скорость и время падения. V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с Зная скорость, применяем эту формулу: t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с Либо используя только высоту и ускорение: t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с Где нужны знания о свободном падении?Они могут понадобиться:
Источник Ускорение свободного падения
Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Же»), — ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационного притяжения планеты (или другого астрономического тела) и сил инерции, вызванных её вращением, за исключением кориолисовых сил инерции [1] . В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы. Значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с² [2] , а в технических расчётах обычно принимают g = 9,81 м/с² . Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря. Реальное ускорение свободного падения на поверхности Земли зависит от широты, времени суток и других факторов. Оно варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах [3] . Оно может быть вычислено (в м/с²) по эмпирической формуле: где СодержаниеВычисление ускорения свободного падения
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центробежного ускорения. Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету однородным шаром массой M и вычислив гравитационное ускорение на расстоянии её радиуса R :
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли (масса М = 5,9736·10 24 кг , радиус R = 6,371·10 6 м ), мы получим Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. Отличия обусловлены:
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной. Перегрузки«Же» используется в космонавтике, авиации, автоспорте, а также вообще в технике как единица измерения перегрузок — увеличения веса тела, вызванного его движением с ускорением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 g [источник не указан 69 дней] . Обычный человек может выдерживать перегрузки до 5 g [источник не указан 769 дней] . Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g . Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при −2. -3 g в глазах «краснеет» и человек тяжелее переносит такую перегрузку из-за прилива крови к голове. В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0 g , но в таблице ниже этот же случай рассматривается как перегрузка в 1 g . Похожий казус происходит также и при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме. Источник ➤ Adblockdetector |
 Задачи с решениями
Задачи с решениями 

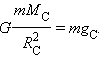
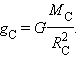
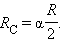
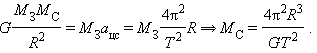





 — широта рассматриваемого места,
— широта рассматриваемого места,  — высота над уровнем моря в метрах. [4] Эта формула применима лишь в ограниченном диапазоне высот от 0 до нескольких десятков км, где убывание ускорения свободного падения с высотой можно считать линейным (на самом же деле оно убывает квадратично).
— высота над уровнем моря в метрах. [4] Эта формула применима лишь в ограниченном диапазоне высот от 0 до нескольких десятков км, где убывание ускорения свободного падения с высотой можно считать линейным (на самом же деле оно убывает квадратично). ,
, м/с².
м/с².