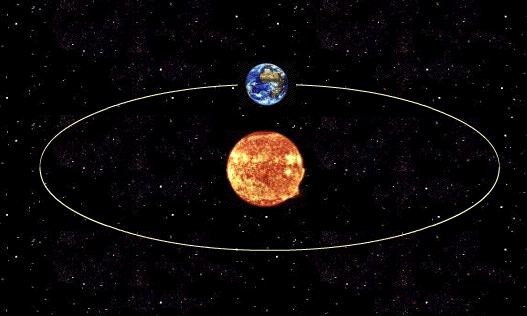
Понятие об угловой скорости: вращение Земли вокруг своей оси и вокруг Солнца
Движение нашей планеты в космическом пространстве можно охарактеризовать двумя типами вращения: вокруг собственной оси и вокруг Солнца. В данной статье рассматривается понятие угловой скорости, приводятся необходимые формулы для вычисления этой величины, а также дается расчет скорости угловой вращения Земли вокруг своей оси и вокруг нашей звезды.
Что такое угловая скорость вращения?
Когда рассматривают перемещение тела в пространстве на большие расстояния, то, как правило, пренебрегают его размерами. В этом случае вводят понятия пути и скорости его движения. Если же решают задачу движения тела вокруг некоторой точки или оси вращения, то пройденный путь всегда равен длине соответствующей окружности, а линейная скорость перемещения заменяется использованием скорости угловой.
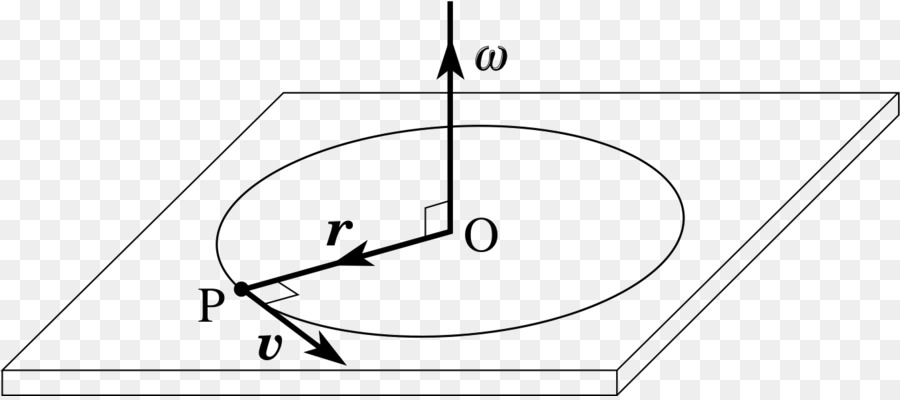
Угловая скорость вращения представляет собой угол, на который тело поворачивается вокруг соответствующей оси за единицу времени. Исходя из этого определения, единицей измерения рассматриваемой величины будут радианы в секунду (рад/с). Также можно использовать градусы в секунду (˚/c). Обозначается угловая скорость греческой буквой омега ω.
Основные формулы
Прежде чем переходить к вопросу, чему равна скорость вращения Земли угловая, следует познакомиться с основными формулами, описывающими эту величину.
Как известно, угловая мера всей окружности составляет 360 ˚ или 2×π радиан, где π = 3,1416. Если тело совершает вокруг оси полный оборот за время T, тогда можно записать следующее выражение:
Время T называют периодом обращения, а величина f = 1/T показывает, сколько оборотов тело сделает за единицу времени, то есть характеризует частоту его вращения.
Еще одной важной формулой для угловой скорости является выражение, объединяющее линейную скорость и радиус вращения:
Если проверить единицу измерения ω в этом выражении, то получаем те же радианы в секунду (с -1 ). Формула показывает, что чем меньше расстояние от оси вращения до тела (r), и чем больше его скорость линейная (v), тем больше будет ω.
Из этой формулы можно легко выразить величину v: v = ω×r. Поскольку угловая скорость является величиной постоянной для некоторого рассматриваемого тела, то быстрее будут двигаться те точки, которые находятся дальше от оси вращения.
Рассмотренные формулы и понятия используем для определения скорости угловой вращения Земли вокруг оси и вокруг Солнца.
Вращение нашей планеты вокруг оси
Каждый человек знает, что планета, на которой он живет, вращается вокруг своей оси, причем экваториальная плоскость Земли наклонена под углом 23˚ к плоскости эклиптики.
Как рассчитать угловую скорость вращения вокруг своей оси Земли? Для этого можно воспользоваться совершенно любой из формул, которые приведены были выше. Поскольку мы знаем, что один оборот вокруг оси происходит за 24 часа, то для расчета следует использовать выражение с периодом T. Получаем:
Здесь значение периода T было переведено в секунды. Полученное значение является небольшим.
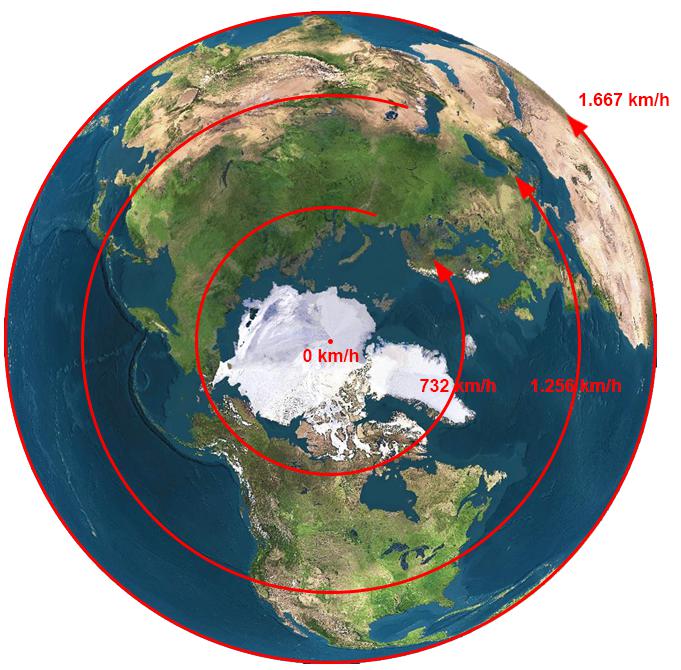
Представляет интерес рассчитать, с какой линейной скоростью движутся точки на поверхности планеты на широте 0˚ (экватор). Экваториальный радиус Земли равен 6 378 000 м. Подставляя это значение в формулу для скорости, получим:
v = ω×r = 7,27×10 -5 ×6 378 000 = 463,8 м/с = 1670 км/ч.
Полученное значение является большим в сравнении со скоростями, которые мы наблюдаем в жизни. Человек эту скорость не ощущает, поскольку вращается вместе с воздухом и почвой под ногами с одной скоростью, то есть он покоится относительно них.
Рассмотренное вращение Земли приводит не только к возникновению явления дня и ночи, но и к появлению так называемой силы Кориолиса, которая оказывает влияние на некоторые земные процессы, например, изменяет направление ветров.
Вращение Земли по своей орбите
Рассчитаем теперь угловую скорость вращения Земли вокруг Солнца. Для этого воспользуемся следующими данными: точное значение сидерического периода обращения нашей планеты по орбите составляет 365 дней 6 часов 9 минут и 9,7632 секунды, то есть T = 31558149,7632 секунд. Теперь можно воспользоваться формулой:
ω = 2×π/T = 2×3,1416/(31558149,7632) = 1,991×10 -7 рад/с.
То есть угловая орбитальная скорость нашей планеты меньше на 1,5 порядка, чем аналогичная величина для вращения вокруг собственной оси. Вычислим линейную скорость, учитывая, что средний радиус орбиты равен 149 597 871 000 метров:
v = ω×r = 1,991×10 -7 ×149 597 871 000 = 29784,8 м/с = 107 225 км/ч.
С этой огромной скоростью наша планета движется в космическом пространстве вокруг Солнца.
С орбитальным движением планеты и наклоном ее оси связано существование времен года в Северном и Южном полушариях.
Источник
Угловая скорость вращения планет вокруг солнца
© Юдин Виктор Васильевич
Ульяновский филиал ИРЭ им. В.А. Котельникова РАН.
1. Угловые скорости планет
В настоящее время существует много гипотез и моделей, объясняющих механизм вращения планет вокруг своей оси. Некоторые модели основаны на взаимодействии магнитных полей, температурных полей и гидросферы планет. Однако приведенные модели не универсальны из-за различного строения и физических характеристик планет. Другие модели и гипотезы приписывают величине угловой скорости вращения планет вокруг своей оси случайный характер, а планеты вращаются только по инерции. В качестве причин приводят столкновения планет с другими небесными телами, приводящие к замедлению или увеличению угловой скорости вращения планет. В настоящей работе выявлена закономерность между угловыми скоростями вращения планет и величинами их диаметров. На этом основании предлагается гипотеза о наличии силового поля, источником которого является Солнце и антигравитационном действии поля на водород в составе планет.
Составим таблицу 1, содержащую необходимые нам физические характеристики планет (обычных и карликовых) Солнечной системы, вращающихся вокруг Солнца по гелиоцентрическим орбитам.
Физические характеристики планет
Радиус планеты r i , км
Период вращения вокруг своей оси, Т i
Угловая скорость вращения планеты ωi =2π/ Тчас,
Радиус гелиоцентрической орбиты R ,а.е.


Меркурий
58,7 суток
1 ,808·10 -6
23час. 56 мин. 4,1 сек
4,108·10 -5
24 час. 37 мин.
7,507·10 -5
9 час. 4 мин.
1 ,438·10 -3
9 час. 55 мин.
8,866·10 -6
10 час.40 мин.30 сек.
9,751·10 -6
16 час. 03 мин.
1 ,609·10 -5
Направление вращения вокруг своей оси приведенных в таблице планет совпадает с направлением вращения Солнца. В таблице опущены планеты, которые имеют противоположное направление вращения. Механизм вращения этих планет рассмотрим далее отдельно.
Построим график зависимости угловой скорости вращения планет ω = 2π/ T час с размерностью [ч -1 ] от расстояния до Солнца R в астрономических единицах [а.е.], как показано на рис. 1.

Зависимость угловых скоростей вращения ω планет от радиуса гелиоцентрической орбиты R имеет вид ломанной кривой.

Вычислим отношения 

Видно, что точки прямо пропорциональной зависимости (1) лежат на гладкой линии. Небольшое увеличение угловой скорости вращения дальше орбиты Юпитера совпадает с увеличением скорости ветров на планетах. Так, на Юпитере ветра дуют со скоростью 167 м/с; на Сатурне – 500 м/с; на Нептуне – 583 м/с. Ось вращения Урана лежит на плоскости гелиоцентрической орбиты и скорость ветра не попадает в интервал между 500 м/с и 583 м/с и составляет 240 м/с.
Таким образом, угловая скорость вращения произвольно выбранной планеты ωпл на разных орбитах будет определяться из отношения 

Чтобы показать, что угловые скорости не являются случайными величинами, изменим произвольно одну из характеристик планет, например, изменим диаметр Марса до 5000 км, а Сатурна до 50000 км. Произойдет нарушение гладкости кривой угловой скорости ωпл, как показано на рис. 3 пунктирными линиями.
Из рис. 2 видно, что вокруг Солнца существует шаровая поверхность на расстоянии примерно 2,7 а.е. от Солнца (пояс астероидов), при попадании на которую планеты имеют наибольшую угловую скорость вращения вокруг своей оси, что может привести к её разрушению, аналогично разрыву махового колеса при превышении предельной скорости вращения.
2. Солнце как источник силового поля
Для объяснения природы силового поля, источником которого является Солнце, обратимся к работе Чернина А.Д. (Чернин А.Д. Космический вакуум./Успехи физических наук, том 171, № 11, ноябрь 2001 г. С. 1153-1175). Перечислим основные свойства космического вакуума, приведенные в работе. Космический вакуум характеризуется плотностью потока энергии и отрицательным давлением, приводящим к антигравитационному эффекту. Космический вакуум присутствует в макро и микро мире. Он входит в состав частиц материи и атомов вещества. В первые мгновения образования Вселенной после взрыва в результате квантовых флуктуаций космического вакуума образовались частицы материи. Плотность космического вакуума со временем уменьшается. Первоначальная плотность космического вакуума была близка к бесконечному значению. Оценки величины плотности на всех этапах существования Вселенной разными исследователями не совпадают. Плотность современного космического вакуума во Вселенной постоянна.
Далее дополним свойства космического вакуума применительно к предлагаемой модели образования силового поля. Поскольку плотность космического вакуума в первый момент жизни Вселенной была очень высока и намного порядков превышала плотность космического вакуума в настоящее время, то можно предположить, что частицы материи сохранили высокую плотность энергии первоначального вакуума. В результате ядерных превращений (например, термоядерная реакция в недрах Солнца), освобождается энергия космического вакуума, заключенная в частицах материи. Солнце становится источником космического вакуума. Образуется потенциальное поле энергии W с наибольшим значением в недрах Солнца и уменьшающее при удалении от Солнца. Возникает градиент плотности энергии космического вакуума в пределах звездной системы. Силовые линии поля в результате вращения Солнца имеют форму дуг. На рис. 2 приведена монотонная кривая sinγ , где γ – угол между касательной к силовой линии поля, проведенной через центр планеты, и радиусом гелиоцентрической орбиты планеты R . В приближении для данной модели силовые линии поля совпадают с траекторией солнечного ветра. Градиент энергии связан с силой 

Антигравитационное свойство космического вакуума проявляется через наблюдаемое расширение водородных образований. Водород является основным материалом Вселенной. Его доля составляет 92% всех атомов, доля гелия – 8% и доля всех остальных элементов менее 0,1%.
Доля водорода в планетах Солнечной системы разная. Распределение водорода по планетам подчиняется закономерности, выявленной Лариным В.Н (см., например, Ларин В.Н. Наша Земля. Москва, “Агар”, 2005, стр. 17-29). Он показал, что при формировании протопланетного диска из-за высокого потенциала ионизации водород беспрепятственно проходил через силовые линии магнитного поля небулы (Протосолнца). В результате в планетах, ближе расположенных к Солнцу, содержится наименьшее отношение массы водорода МН к общей массе планеты 


Зависимость ωпл = ωЗ на рис. 2 можно получить, если её представить в виде произведения трёх основных монотонных функций от аргумента R , а именно,
ωпл = 
где: 


Силовое поле действует на атомы водорода в составе планеты и выталкивает водород в противоположное от Солнца направление. Чем больше водорода в объеме планеты и чем ближе планета расположена к Солнцу, тем больше результирующая выталкивающая сила. Надо отметить, что Юпитер и Сатурн содержат большее отношение массы водорода к общей массе планеты 
4. Динамика вращения планет Солнечной системы
Рассмотрим силы, действующие на планету Солнечной системы с учетом наличия силового поля, источником которого является Солнце, как показано на рис. 4. Для наглядности выразим силу, действующую на водород в составе планеты, через введенное ускорение 
Чем ближе к центру Солнца, тем выше скорость вращения вещества Солнечной системы. Известно расхождение между линейными скоростями движения планет по орбитам и линейной скоростью вращения поверхности Солнца. Все планеты Солнечной системы вращаются вокруг Солнца в одном направлении по своим орбитам. Независимо от их массы скорости движения планет по орбитам определяют по формуле

где; G – гравитационная постоянная; M С – масса Солнца; R – расстояние от Солнца до планеты. Скорость движения планеты выводится из равенства центробежной силы
F Ц = 
и силы Ньютона взаимного притяжения планеты и Солнца
F Н = 
где М – масса планеты. Линейная скорость поверхности Солнца составляет V / = 2 км/с, а вычисленная по формуле (2) составляет V = 437 км/с. Считается, что скорость вращения Солнца является аномально низкой, по-видимому потому, что для всех объектов Солнечной системы, вращающихся по гелиоцентрическим орбитам, формула (2) верно описывает линейные скорости движения, а в одном случае (для Солнца) – нет. Но в Солнце сосредоточено 99,866% массы Солнечной системы, и оно определяет динамику движения планет. Итак, исходя из линейной скорости поверхности Солнца V / = 2 км/с, центробежная сила планет должна иметь величину 

Рассмотрим силы, действующие на планету при её вращении вокруг Солнца, приняв за систему отсчета абсолютную систему координат с началом отсчета в центре Солнца. Центробежная сила 




Равнодействующая сила равна F ∑ = FW + F τ и направлена по линии R . Действительная величина центробежной силы равна сумме сил F Ц = 

Величина радиуса R орбиты планеты зависит от отношения массы водорода в составе планеты к общей массе планеты МН/М. На одной и той же орбите могут находиться планеты с разными массами но с одинаковым отношением МН/М. Для конкретного отношения МН/М, присущего определенной планете, существует только одно положение её на линии R , в котором равнодействующая F ∑ совпадает по направлению с этой линией. Во всех других положениях планеты направление равнодействующей силы F ∑ будет отклоняться от линии R . При условии а>аτ сила 

Таким образом, силовое поле способствует увеличению центробежной силы планет, увеличивает линейные скорости планет и удерживает планеты на орбитах.
Отметим, что приведенная система сил не является единственной для описания положения объектов Солнечной системы и применима только к относительно большим объектам с шаровой поверхностью и содержащим водород.
Как показано на рис. 5 вращение планеты, движущейся по линии L вокруг Солнца, возможно только за счет разности ускорений поля по линии, перпендикулярной силовым линиям поля. Угол наклона γ создает разность ускорения ∆а на западе З и востоке В планеты и вызывает момент сил, который вращает планету в направлении с востока на запад с угловой скоростью 
На рис. 5 видно, что если водород распределен по поверхности планеты, то величину угловой скорости определяет диаметр планеты D . С увеличением диаметра планеты плечо момента сил увеличивается. Для планет с распределением водорода по объему, угловую скорость вращения определяет эквивалентный диаметр, который меньше диаметра планеты D .

В январе и июле происходит увеличение угловой скорости вращения Земли вокруг своей оси, причем в июле больше, чем в январе ( http://fiz.1september.ru/ 2003/01/no01_1.htm ). В июле Земля находится в афелии, т.е. наибольше удалена от Солнца, а в январе находится в перигелии и наименьше удалена от Солнца, как показано на рис. 6. Разность расстояний составляет 5 млн. км ( http://mir24.tv/ news/Science/5196805 ). Равнодействующая FW параллельных сил, действующих по линии ускорений а, смещена к внутренней линии l вн действия силового поля. При приближении к Солнцу равнодействующая FW увеличивается, а длина плеча r уменьшается. Однако момент силы FW · r может быть больше момента сил при нахождении планеты на среднем расстоянии от Солнца, так как увеличение силы FW будет превосходить уменьшение длины плеча r . При удалении планеты равнодействующая FW уменьшается, а длина плеча r увеличивается за счет того, что ускорение а по линии l нар уменьшается быстрее, чем по линии l вн . Увеличение длины плеча r будет превосходить уменьшение силы FW , что приведет к увеличению момента сил относительно действующего на среднем расстоянии. Таким образом, и при приближении, и при удалении планеты от Солнца, угловая скорость планет увеличивается.
Определить числовые характеристики поля можно путем запуска на гелиоцентрическую орбиту спутников с заданными различными относительными массами водорода со скоростями, соответствующим скоростям на данной орбите. На орбиту выводят не менее двух искусственных спутников Солнца с известными одинаковыми массами спутников, но с разными массами водорода в каждом из них. Определяют отклонение спутников от орбиты.
При подтверждении действия силового поля на водород в составе планеты, можно будет запускать искусственные спутники Солнца на устойчивые орбиты со временем жизни миллиарды лет и создавать заселенные искусственные планеты.
Обратное вращение планет
Рассмотрим систему сил вращения Венеры вокруг своей оси с использованием модели силового поля. Ускорение поля действует на водородосодержащие облака планеты. Под влиянием радиационного нагрева облака Венеры со стороны Солнца будут иметь большее давление, чем на ночной стороне. В результате выравнивания давлений на ночной стороне Венеры сосредоточено больше по массе облаков, чем на дневной.
Зонд “Венера-экспресс”, используя звёздные затмения, показал, что атмосферная дымка Венеры простирается гораздо выше на ночной стороне по сравнению с дневной. На дневной стороне облачный слой имеет толщину 20 км и простирается приблизительно до 65 км, тогда как на ночной стороне облачный слой в форме плотного тумана достигает 90 км в высоту, проникая в мезосферу и даже выше (105 км), уже как прозрачная дымка ( http://ru.wikipedia.org/wiki/ Атмосфера_Венеры ).

Гравитационное взаимодействие Венеры с Солнцем осуществляется по прямой R в противоположном направлении (рис. 7). Количество водорода на левой стороне по направлению поля q больше, чем на правой, Сила, действующая на ночные облака слева равна F 1 = m лев ·а1 и больше силы F 2 = m прав ·а2 , действующей на облака вправо и вращение облаков происходит в обратном направлении, по сравнению с направлением вращения планет Солнечной системы вокруг своей оси. За счет сил трения в условиях больших температур на поверхности планеты вращение облаков будет увлекать за собой планету.
Твердое вещество планеты из-за незначительного количества водорода в его составе, имеет меньший момент вращения, чем момент вращения облаков. Момент вращения твердого вещества планеты совпадает с моментами вращения планет Солнечной системы и направлен встречно моменту вращения облаков. Это объясняет, почему передача движения облаками твердому веществу планеты недостаточна и ниже расчетного значения ( http://space-horizon.ru/articles/14 ).
Мониторинг подземных источников воды и углеводородов
Если водород по планете распределен неравномерно (Земля и Марс), то ось вращения планеты поворачивается на угол α. Меркурий и Венера имеют наименьшие наклоны, так как водород равномерно распределен по объему. Но не только характер распределения водорода по поверхности планеты влияет на наклон оси вращения, но и плотность газовых планет. Из-за низкой плотности газовой оболочки Урана его ядро сместилось в сторону Солнца ввиду сил взаимного притяжения, а газовая водородосодержащая оболочка сместилась в противоположную от Солнца сторону. У Плутона также следует ожидать разные центры масс каменного ядра и ледяной мантии, что привело к наклону оси вращения и заставило вращать планету в обратную сторону.
Для Земли угол наклона α составляет 23,5 0 (рис. 8). Силовое поле старается повернуть центр масс водорода. Проведенная оценка расположения центра массы ЦМ водорода показала, что он лежит на радиусе r З Земли с координатами геометрического центра Ц на поверхности Земли 170 0 восточной долготы и 50 0 южной широты.

На рис. 8 показано, что силовые линии поля со стороны Солнца в зимний период в северном полушарии Земли (на рисунке с левой стороны), стремятся переместить центр масс ЦМ на горизонтальную линию. А в летний период (на рисунке с правой стороны), стремятся вернуть центр масс ЦМ в прежнее положение, и центр масс водорода занимает среднее положение близкое по значению к 23,5 0 южной широты. Центр масс воды не может точно совпадать с реальным углом наклона 23,5 0 , так как на величину отклонения влияют места расположения водородосодержащих веществ в недрах Земли.
Можно предположить, что непрерывные процессы перемещения материков приводит к перераспределению центра масс водной поверхности и к изменению угла наклона оси вращения Земли.
На Марсе чередование материков и океанов из водородосодержащих веществ, скрытых под слоем поверхности планеты, также приводит к смещению центра масс водорода. Известно, что заметную часть поверхности Марса занимает возвышенность с самой высокой горой Солнечной системы Олимп.
Аналогично, на газовых планетах, из-за смещения центра масс плотного ядра в результате гравитационного взаимодействия с Солнцем и центра масс газообразной и жидкой фаз водорода и водородосодержащих веществ в результате обратного по направлению воздействия силового поля, приводит к наклону оси вращения.
Эффект действия поля на водород планет можно использовать при прогнозировании и разведке подземных вод и углеводородного топлива в местах с их наибольшей концентрацией. Для этого необходимо точное измерение угла наклона оси вращения Земли и координаты центра масс поверхностных вод.
Оценка количества водорода на планетах Солнечной системы
Под планетой будем понимать собственно планету и её атмосферу. Самая близкая к Солнцу планета Меркурий содержит наименьшее количество водорода в составе вещества планеты. Поверхность Меркурия образуют силикаты (кристаллогидраты), имеющие химическую связь с молекулами воды mSiO 2 · nH 2 O (глина, слюда), глина каолинит Al 2 O 3 ·2 SiO 2 ·2 H 2 O и другие. Слой силикатов имеет толщину до 600 км. Водород также растворен в железном ядре планеты.
Венера известна самыми плотными облаками. У Венеры водород большей частью входит в состав водяного пара, по весу равному 3·10 -5 массы планеты. Отношение МН/М равно 3,3·10 -6 . Вещество планеты Венеры состоит из базальта, содержащего незначительное количество водорода. Вода в недрах планеты составляет 3·10 -9 массы планеты ( http://space-horizon.ru/articles/14 ). Можно считать, что на Венере по сравнению с Меркурием отношение МН/М больше.
Массу воды на Земле оценивают в 2,176·10 21 кГ. Общее количество водорода составляет 2,418·10 20 кГ, а отношение МН/М равно 0,3·10 -4 .
Известно, что на Марсе имеется как вода, так и аммиак. Аммиак в весовом соотношении содержит водорода больше, чем содержит вода. Плотность Марса в два раза меньше плотности земли и можно предположить, что водородосодержащих веществ скрыто под верхним слоем поверхности намного больше. Интерполируя отношение МН/М от расстояния R примем отношение МН/М Марса равным 0,6·10 -4 .
Церера – карликовая планета в поясе астероидов. При диаметре 950 км имеет ледяную мантию толщиной 100 км. Отношение МН/М будет около 0,1.
Юпитер – газовый гигант, на 82 % состоит из газа, остальное льды и твердая порода. Предполагается, что гелий и водород находятся в соотношении 30% и 70%. При больших давлениях водород Юпитера и Сатурна переходит в фазу металлического водорода с отличными от неметаллического водорода свойствами. Вероятнее всего, что силовое поле не оказывают механического действия на металлический водород как и на другие элементы. Водород, на который действует силовое поле, сосредоточен в верхнем слое планеты толщиной 21 тыс. км (http://ru.wikipedia.org/wiki/Юпитер). Сатурн по составу вещества аналогичен Юпитеру. У Сатурна водород, на который действует силовое поле, сосредоточен в верхнем слое толщиной 30 тыс. км (http://ru.wikipedia.org/wiki/Сатурн). По оценке отношение МН/М у Сатурна больше, чем у Юпитера и в нашей модели отношение примем равным 0,2.
В состав газовых планет Уран и Нептун входит мантия, богатая водой. Примем, что отношение МН/М у Нептуна выше, чем у Урана, так как масса мантии Урана составляет до 13,5 масс Земли ( http://ru.wikipedia.org/wiki/Уран_(планета) ), а масса мантии Нептуна составляет до 15 масс Земли ( http://ru.wikipedia.org/wiki/Нептун ). По оценке отношение МН/М у Урана выше, чем у Сатурна и составляет 0,25.
Наибольшее отношение МН/М у астероида Плутона, который состоит из водяных льдов и скальной породы. Далее на расстоянии 55 а.е. от Солнца расположен пояс Койпера, состоящий только из аммиачных, метановых и водяных льдов.
Источник
➤ Adblockdetector