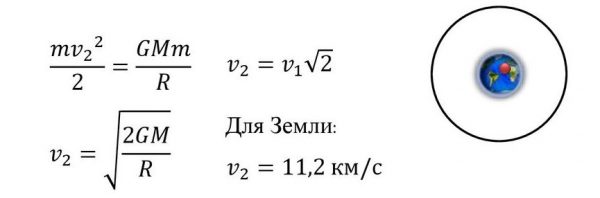Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
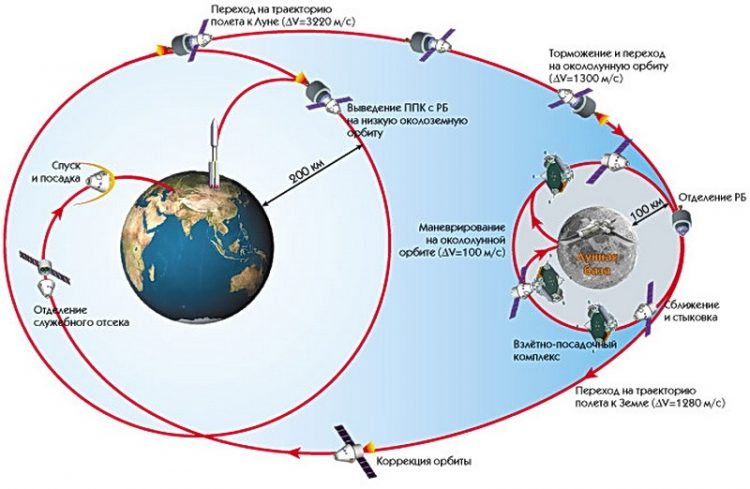
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
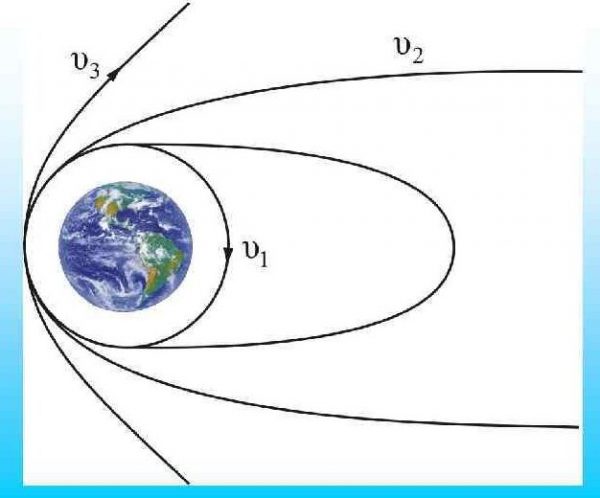
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
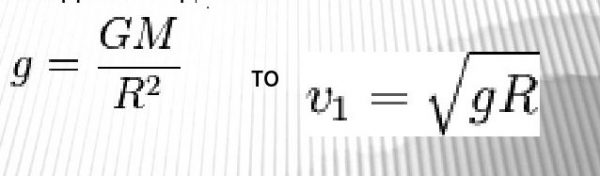
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
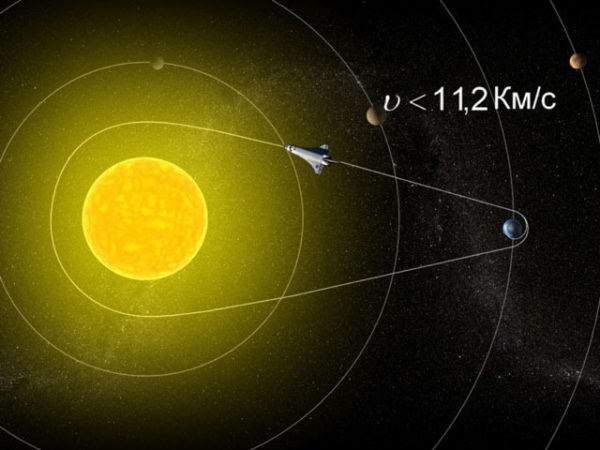
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник
Траектория движения спутников солнца
§ 14. Д вижение небесных тел под действием сил тяготения
1. Закон всемирного тяготения
С огласно закону всемирного тяготения, изученному в курсе физики,
все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
F = G 
,
где m 1 и m 2 — массы тел; r — расстояние между ними; G — гравитационная постоянная.
Открытию закона всемирного тяготения во многом способствовали законы движения планет, сформулированные Кеплером, и другие достижения астрономии XVII в. Так, знание расстояния до Луны позволило Исааку Ньютону (1643—1727) доказать тождественность силы, удерживающей Луну при её движении вокруг Земли, и силы, вызывающей падение тел на Землю.
Ведь если сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна, находящаяся от Земли на расстоянии примерно 60 её радиусов, должна испытывать ускорение в 3600 раз меньшее, чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с 2 . Следовательно, ускорение Луны должно составлять 0,0027 м/с 2 .
В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение
где ω — угловая скорость Луны; r — радиус её орбиты. Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять r = 60 • 6 400 000 м = 3,84 • 10 8 м. Звёздный период обращения Луны T = 27,32 суток, в секундах составляет 2,36 • 10 6 с. Тогда ускорение орбитального движения Луны
a = 
• r = 
• 3,84 • 10 8 м = 0,0027 м/с 2 .
Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.
Можно убедиться и в том, что при движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения. Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит d и квадратов периодов обращения T есть величина постоянная:
= 
= 
= . = const.
Ускорение планеты равно
a = 
= 
= 4 π 2 
.
Из третьего закона Кеплера следует
= 
,
поэтому ускорение планеты равно
a = 4 π 2 • const 
.
Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения.
2. Возмущения в движении тел Солнечной системы
З аконы Кеплера строго выполняются, если рассматривается движение двух изолированных тел (Солнце и планета) под действием их взаимного притяжения. Однако в Солнечной системе планет много, все они взаимодействуют не только с Солнцем, но и между собой. Поэтому движение планет и других тел не в точности подчиняется законам Кеплера. Отклонения тел от движения по эллипсам называются возмущениями .
Возмущения эти невелики, так как масса Солнца гораздо больше массы не только отдельной планеты, но и всех планет в целом. Наибольшие возмущения в движении тел Солнечной системы вызывает Юпитер, масса которого в 300 раз превышает массу Земли. Особенно заметны отклонения астероидов и комет при их прохождении вблизи Юпитера.
В настоящее время возмущения учитываются при вычислении положения планет, их спутников и других тел Солнечной системы, а также траекторий космических аппаратов, запускаемых для их исследования. Но ещё в XIX в. расчёт возмущений позволил сделать одно из самых известных в науке открытий «на кончике пера» — открытие планеты Нептун.
Проводя очередной обзор неба в поиске неизвестных объектов, Вильям Гершель в 1781 г. открыл планету, названную впоследствии Ураном. Спустя примерно полвека стало очевидно, что наблюдаемое движение Урана не согласуется с расчётным даже при учёте возмущений со стороны всех известных планет. На основе предположения о наличии ещё одной «заурановой» планеты были сделаны вычисления её орбиты и положения на небе. Независимо друг от друга эту задачу решили Джон Адамс в Англии и Урбен Леверье во Франции. На основе расчётов Леверье немецкий астроном Иоганн Галле 23 сентября 1846 г. обнаружил в созвездии Водолея неизвестную ранее планету — Нептун. Это открытие стало триумфом гелиоцентрической системы, важнейшим подтверждением справедливости закона всемирного тяготения. В дальнейшем в движении Урана и Нептуна были замечены возмущения, которые стали основанием для предположения о существовании в Солнечной системе ещё одной планеты. В 1930 г. после просмотра большого количества фотографий звёздного неба был обнаружен Плутон, который, как оказалось, является одним из множества объектов, расположенных за орбитой Нептуна.
3. Масса и плотность Земли
З акон всемирного тяготения позволил определить массу нашей планеты. Исходя из закона всемирного тяготения, ускорение свободного падения можно выразить так:
g = G 
.
Подставим в формулу известные значения этих величин: g = 9,8 м/с 2 , G = 6,67 • 10 –11 Н • м 2 /кг 2 , R = 6370 км — и получим, что масса Земли M = 6 • 10 24 кг.
Зная массу и объём земного шара, можно вычислить его среднюю плотность: 5,5 • 10 3 кг/м 3 . С глубиной за счёт увеличения давления и содержания тяжелых элементов плотность возрастает.
4. Определение массы небесных тел
Б олее точная формула третьего закона Кеплера, которая была получена Ньютоном, даёт возможность определить одну из важнейших характеристик любого небесного тела — массу. Выведем эту формулу, считая (в первом приближении) орбиты планет круговыми.
Пусть два тела, имеющие массы m 1 и m 2 , взаимно притягивающиеся и обращающиеся вокруг общего центра масс, находятся от центра масс на расстоянии r 1 и r 2 и обращаются вокруг него с периодом T . Расстояние между их центрами R = r 1 + r 2 . На основании закона всемирного тяготения ускорение каждого из этих тел равно:
a 1 = G 
, a 2 = G 
.
Угловая скорость обращения вокруг центра масс составляет ω = 
. Тогда центростремительное ускорение выразится для каждого тела так:
a 1 = 
r 1 , a 2 = 
r 2 .
Приравняв полученные для ускорений выражения, выразив из них r 1 и r 2 и сложив их почленно, получаем:
G = 
= 
( r 1 + r 2 ),
= 
.
Поскольку в правой части этого выражения находятся только постоянные величины, оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, — Солнце и планета, планета и спутник. Определим массу Солнца, для этого запишем выражение:
= 
,
где M — масса Солнца; m 1 — масса Земли; m 2 — масса Луны; T 1 и a 1 — период обращения Земли вокруг Солнца (год) и большая полуось её орбиты; T 2 и a 2 — период обращения Луны вокруг Земли и большая полуось лунной орбиты.
Пренебрегая массой Земли, которая ничтожно мала по сравнению с массой Солнца, и массой Луны, которая в 81 раз меньше массы Земли, получим:
= 
.
Подставив в формулу соответствующие значения и приняв массу Земли за единицу, мы получим, что Солнце примерно в 333 тыс. раз по массе больше нашей планеты.
Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях. Об определении массы звёзд см. в § 23.
П од действием взаимного притяжения частиц тело стремится принять форму шара. Если эти тела вращаются, то они деформируются, сжимаются у полюсов.
Кроме того, изменение их формы происходит и под действием взаимного притяжения, которое вызывают явления, называемые приливами . Давно известные на Земле, они получили объяснение только на основе закона всемирного тяготения.
Рис. 3.13. Схема лунных приливов
Рассмотрим ускорения, создаваемые притяжением Луны в различных точках земного шара (рис. 3.13). Поскольку точки A , B и O находятся на различных расстояниях от Луны, ускорения, создаваемые её притяжением, будут различны.
Разность ускорений, вызываемых притяжением другого тела в данной точке и в центре планеты, называется приливным ускорением.
Приливные ускорения в точках A и B направлены от центра Земли. В результате Земля, и в первую очередь её водная оболочка, вытягивается в обе стороны по линии, соединяющей центры Земли и Луны. В точках A и B наблюдается прилив, а вдоль круга, плоскость которого перпендикулярна этой линии, на Земле происходит отлив. Тяготение Солнца также вызывает приливы, но из-за большей его удалённости они меньше, чем вызванные Луной. Приливы наблюдаются не только в гидросфере, но и в атмосфере и в литосфере Земли и других планет.
Вследствие суточного вращения Земля стремится увлечь за собой приливные горбы, в то же время вследствие тяготения Луны, которая обращается вокруг Земли за месяц, полоса приливов должна перемещаться по земной поверхности значительно медленнее. В результате между огромными массами воды, участвующей в приливных явлениях, и дном океана возникает приливное трение. Оно тормозит вращение Земли и вызывает увеличение продолжительности суток, которые в прошлом были значительно короче (5—6 ч). Тот же эффект ускоряет орбитальное движение Луны и приводит к её медленному удалению от Земли. При этом приливы со стороны Земли на Луне затормозили её вращение, и она теперь обращена к Земле одной стороной. Такое же медленное вращение характерно для многих спутников Юпитера и других планет. Сильные приливы, вызываемые на Меркурии и Венере Солнцем, по-видимому, являются причиной их крайне медленного вращения вокруг оси.
6. Движение искусственных спутников Земли и космических аппаратов к планетам
В озможность создания искусственного спутника Земли теоретически обосновал ещё Ньютон. Он показал, что существует такая горизонтально направленная скорость 
, при которой тело, падая на Землю, тем не менее на неё не упадёт, а будет двигаться вокруг Земли, оставаясь от неё на одном и том же расстоянии. При такой скорости тело будет приближаться к Земле вследствие её притяжения как раз на столько, на сколько из-за кривизны поверхности нашей планеты оно будет от неё удаляться (рис. 3.14). Эта скорость, которую называют первой космической (или круговой), известна вам из курса физики:
v 1 = 
= 7,9 • 10 3 м/с = 7,9 км/с.
Рис. 3.14. Орбита искусственного спутника Земли
Практически осуществить запуск искусственного спутника Земли оказалось возможно лишь через два с половиной столетия после открытия Ньютона — 4 октября 1957 г. За время, прошедшее с этого дня, который нередко называют началом космической эры человечества, искусственные спутники самого различного устройства и назначения заняли важное место в нашей повседневной жизни. Они обеспечивают непрерывный мониторинг погоды и других природных явлений, трансляции телевидения и т. п. Спутниковая навигационная система ГЛОНАСС и другие системы глобального позиционирования позволяют в любой момент с высокой степенью точности определить координаты любой точки на Земле. Пожалуй, нет в наши дни ни одной глобальной проблемы, в решении которой не принимали участие искусственные спутники Земли (ИСЗ).
Космические аппараты (КА), которые направляются к Луне и планетам, испытывают притяжение со стороны Солнца и согласно законам Кеплера так же, как и сами планеты, движутся по эллипсам. Скорость движения Земли по орбите составляет около 30 км/с. Если геометрическая сумма скорости космического аппарата, которую ему сообщили при запуске, и скорости Земли будет больше этой величины, то КА будет двигаться по орбите, лежащей за пределами земной орбиты. Если меньше — то внутри орбиты Земли. В первом случае, если аппарат летит к Марсу (рис. 3.15) или другой внешней планете, энергетические затраты будут наименьшими, если КА достигнет орбиты этой планеты при своём максимальном удалении от Солнца — в афелии. Кроме того, необходимо так рассчитать время старта КА, чтобы к этому моменту в ту же точку своей орбиты пришла планета. Иначе говоря, начальная скорость и день запуска КА должны быть выбраны таким образом, чтобы КА и планета, двигаясь каждый по своей орбите, одновременно подошли к точке встречи. Во втором случае — для внутренней планеты — встреча с КА должна произойти в перигелии его орбиты (рис. 3.16). Такие траектории полётов называются полуэллиптическими . Большие оси этих эллипсов проходят через Солнце, которое находится в одном из фокусов, как и полагается по первому закону Кеплера.
Рис. 3.15. Траектория полёта KA к Марсу
Рис. 3.16. Траектория полёта KA к Венере
Конструкция и оборудование современных КА обеспечивают возможность совершения ими весьма сложных манёвров — выход на орбиту спутника планеты, посадка на планету, передвижение по её поверхности и т. п.
В опросы 1. Почему движение планет происходит не в точности по законам Кеплера? 2. Как было установлено местоположение планеты Нептун? 3. Какая из планет вызывает наибольшие возмущения в движении других тел Солнечной системы и почему? 4. Какие тела Солнечной системы испытывают наибольшие возмущения и почему? 5. По каким траекториям движутся космические аппараты к Луне; к планетам? 6*. Объясните причину и периодичность приливов и отливов. 7*. Будут ли одинаковы периоды обращения искусственных спутников Земли и Луны, если эти спутники находятся на одинаковых расстояниях от них?
У пражнение 12 1. Определите массу Юпитера, зная, что его спутник, который отстоит от Юпитера на 422 000 км, имеет период обращения 1,77 суток. Для сравнения используйте данные для системы Земля—Луна. 2. Ускорение силы тяжести на Марсе составляет 3,7 м/с 2 , на Юпитере — 25 м/с 2 . Рассчитайте первую космическую скорость для этих планет. 3. Сколько суток (примерно) продолжается полёт КА до Марса, если он проходит по эллипсу, большая полуось которого равна 1,25 а. е.?
Источник