Точки лагранжа системы земля солнце

Точки Лагранжа

Как выглядят и где искать точки Лагранжа в космосе: история обнаружения, система Земля и Луна, 5 L-точек системы двух массивных тел, влияние гравитации.

Будем откровенны: мы застряли на Земле. Стоит поблагодарить гравитацию за то, что нас не выкинуло в космическое пространство и мы можем ходить по поверхности. Но чтобы вырваться, приходится прикладывать огромное количество энергии.

Однако, во Вселенной есть определенные регионы, где умная система сбалансировала гравитационное влияние. При правильном подходе это можно использовать для более продуктивного и быстрого освоения пространства.

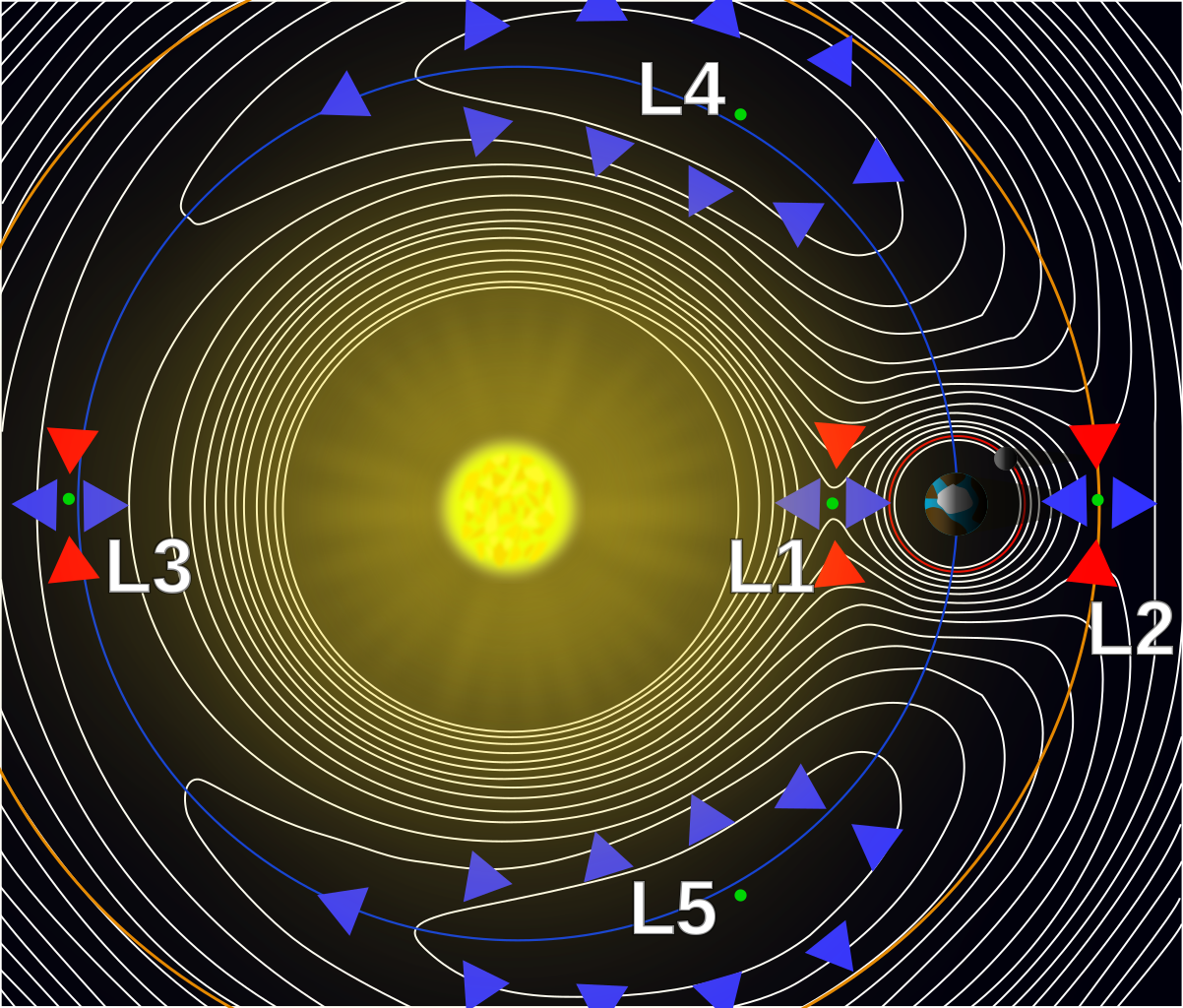
Пять точек Лагранжа в схеме Солнце-Земля

Эти места называют точками Лагранжа (L-точки). Наименование получили от Жозефа Луи Лагранжа, который описал их в 1772 году. Фактически, ему удалось расширить математику Леонарда Ейлера. Ученый первым открыл три таких точки, а Лагранж заявил о следующих двух.

Точки Лагранжа: О чем идет речь?

Когда вы располагаете двумя массивными объектами (например, Солнце и Земля), то их гравитационный контакт замечательно сбалансирован в конкретных 5 участках. В каждом из них можно расположить спутник, который будет удерживаться на месте при минимальных усилиях.

Точки Лагранжа в системе Солнце-Земля

Наиболее примечательная – первая точка Лагранжа L1, сбалансированная между гравитационным притяжением двух объектов. Например, можно установить спутник над поверхностью Луны. Земная тяжесть вталкивает его в Луну, но сила спутника также сопротивляется. Так что аппарату не придется тратить много топлива. Важно понимать, что эта точка есть между всеми объектами.

L2 находится на одной линии с массой, но с другой стороны. Почему же объединенная гравитация не притягивает спутник к Земле? Все дело в орбитальных траекториях. Спутник в точке L2 расположится на более высокой орбите и отстает от Земли, так как перемещается вокруг звезды медленнее. Но земная гравитация подталкивает его и помогает закрепиться на месте.

L3 искать нужно на противоположной стороне от системы. Гравитация между объектами стабилизируется и аппарат с легкостью маневрирует. Такой спутник всегда закрывался бы Солнцем. Стоит отметить, что три описанные точки не считаются устойчивыми, потому любой спутник рано или поздно отклонится. Так что без рабочих двигателей там делать нечего.

Есть также L4 и L5, расположенные спереди и сзади нижнего объекта. Между массами создается равносторонний треугольник, одной из сторон которого будет L4. Если перевернете вверх ногами, то получите L5.

Последние две точки считают стабильными. Это подтверждают найденные астероиды на крупных планетах, вроде Юпитера. Это троянцы, попавшие в гравитационную ловушку между гравитациями Солнца и Юпитера.

Диаграмма, демонстрирующая Юпитер и несколько троянцев

Как использовать такие места? Важно понимать, что существует множество разновидностей космического освоения. Например, в точках Земля-Солнце и Земля-Луна уже расположены спутники.

Солнце-Земля L1 – прекрасное место для проживания солнечного телескопа. Аппарат максимально подошел к звезде, но не теряет связи с родной планетой.

В точке L2 планируют разместить будущий телескоп Джеймса Уэбба (в 1.5 миллионах км от нас).

Художественная интерпретация телескопа Джеймс Уэбб, добывающий информацию об экзопланетах

Земля-Луна L1 – отличная точка для лунной станции по дозаправке, которая позволяет экономить на доставке топлива.

Наиболее фантастической идеей будет желание поставить в L4 и L5 космическую станцию Остров III, потому что там она была бы абсолютной стабильной.

Давайте все же поблагодарим гравитацию и ее диковинное взаимодействие с другими объектами. Ведь это позволяет расширить способы освоения пространства.

Источник

Полет в точку Лагранжа: как устроены самые странные места в Солнечной системе, где практически не работает гравитация

В Солнечной системе существуют места, где практически отсутствует гравитация — точки Лагранжа. Точнее, она там есть — но одновременно от нескольких крупных космических тел, направленная в разные стороны. Поэтому любой небольшой объект, попадающий в эти области, может остаться там на миллиарды лет. «Хайтек» разобрался в истории открытия точек Лагранжа и мистификациях, связанных с ними.

Что такое точка Лагранжа?

В 1772 году математик Жозу Луи Лагранж вычислил в своем исследовании «Проблема трех тел», что гравитационное поле Земли должно нейтрализовать гравитационное притяжение самого большого объекта в Солнечной системе — Солнца — в пяти областях пространства. По сути, эти пять точек являются единственными местами в нашей системе, где практически не работает гравитация благодаря одинаковой силе притяжения от нескольких космических тел.

Всего существуют пять точек Лагранжа — L1, L2, L3, L4 и L5. Для ученых наиболее интересными для изучения являются точки L4 и L5 — единственные стабильные области из всех точек Лагранжа. Если спутник попадет в точки L1 или L2, через несколько месяцев орбиты изменятся и область отсутствия гравитации также сместится, поэтому космическому телу придется совершать различные маневры, чтобы оставаться в этой области.

Точки L4 и L5, которые считаются самыми стабильными, расположены на плоскости земной орбиты на расстоянии 150 млн км от нашей планеты (для сравнения, расстояние от Земли до Луны составляет 383,4 тыс. км, среднее расстояние до Венеры — от 38 до 250 млн км в зависимости от местоположения планет). При этом L4 вращается вокруг Солнца на 60° впереди Земли, а L5 — на 60° позади.

Вокруг других планет в Солнечной системе ученые также наблюдают похожие области. В 1906 году астроном и пионер астрофотографии Максимилиан Вольф обнаружил астероид, который находится постоянно в одном и том же месте за главным поясом астероидов между орбитами Марса и Юпитера.

Этот астероид оказался точкой L4 Юпитера. Ученые назвали его Ахиллесом — именно с него пошла традиция называть все подобные астероиды именами участников Троянской войны. Сейчас благодаря этому открытию астрофизики обнаружили более тысячи астероидов, находящихся в двух стабильных точках Лагранжа Юпитера.

Другое дело, что поиски подобных астероидов вокруг других планет пока оказались не столь успешными: возле Сатурна их пока не обнаружили, а около Нептуна — всего один. Вероятно, пока астрофизики просто не рассчитали правильное местоположение этих областей у таких планет.

Хм. Все равно не очень понятно, как это работает

Точка Лагранжа — это такое место в космосе, где объединенные гравитационные силы двух очень массивных тел — Земли и Солнца или Земли и Луны — равны центробежной силе, ощущаемой намного меньшим третьим телом. Взаимодействие этих сил создает точку равновесия, где может быть навечно «припаркован» условный космический корабль для проведения наблюдений.

Предположим, у нас есть два очень больших объекта в космосе — Земля и Солнце. У них есть гравитационное притяжение. И есть спутник — если мы запускаем его слишком близко к Солнцу, то постепенно гравитация притянет его к звезде, и он либо врежется в нее, либо выйдет на солнечную орбиту. Если к Земле, то спутник либо окажется на околоземной орбите, либо войдет в атмосферу нашей планеты и сгорит в ней.

Точки Лагранжа — места в космосе, где гравитация двух объектов (в нашем случае Солнца и Земли) эффективно компенсирует друг друга. Это позволит спутнику оставаться именно в том месте, куда он был запущен.

Математика так работает, что точки L1, L2, и L3 не являются стабильными. Какое-то время наш спутник, оказавшийся в этих точках, будет находиться внутри областей, но потом гравитация все-таки изменится и наше космическое тело полетит дальше. Это можно сравнить с кусочком мрамора, который мы аккуратно положили на вершину перевернутой чаши. Он там будет лежать, но один удар по столу — и мрамор скатится вниз.

L4 и L5 являются стабильными. Даже если ваш спутник не идеально добрался до этих точек, гравитация в любом случае как бы подтолкнет его в такое положение, чтобы он оставался там навсегда. На этот раз наш мраморный кусочек уже находится на дне чаши, быстро движущейся вправо, поэтому, даже если он не идеально отцентрирован, то переместится в правильное положение.

Хорошо. Как можно использовать точки Лагранжа?

Исследователи в области космонавтики еще в 1970-х годах обратили внимание на точки Лагранжа. Например, в точке L1 системы «Земля — Солнце» можно было бы поместить космическую солнечную обсерваторию. Она никогда не будет попадать в тень Земли, соответственно, наблюдения можно вести без перерыва.

Точка L2 системы «Земля — Солнце» может быть практически идеальной для установки в ней космического телескопа. В ней Земля почти всегда заслоняет солнечный свет и не отражает его в это место, что позволило бы ученым постоянно изучать другие звезды.

В точке L1 системы «Земля — Луна» можно поместить ретрансляционную станцию в период освоения спутника Земли. Станция будет постоянно находиться в зоне прямой видимости для большей части полушария Луны, обращенного к Земле. Поэтому для связи с ней будущим колонистам Луны понадобятся передатчики в десятки раз менее мощные, чем для связи с Землей.

Существует множество проектов, в рамках которых астрофизики планируют тем или иным образом использовать точки Лагранжа в своих исследованиях.

ISEE-3 — первый космический аппарат, выведенный в точку L1 системы «Земля — Солнце». Был запущен еще в 1978 году, в рамках миссии должен был доказать, что существование этих точек либрации (другое название точек Лагранжа — «Хайтек») вообще реально, а также исследовать верхние границы магнитосферы Земли, проходящие как раз на расстоянии около 1,5 млн км от нашей планеты. После этого — через десять лет — зонд был направлен к кометам Галлея и Джакобини — Циннера. Сейчас ISEE-3 несколько десятилетий просто находится в космосе в выключенном состоянии.

В точке L1 системы «Земля — Солнце» сейчас находятся несколько миссий, в том числе зонд для изучения солнечного ветра GGS Wind, станция для изучения гелиосферы SOHO и DSCOVR для анализа выбросов корональной массы.

В точке L2 системы «Земля — Солнце» долго находился спутник WMAP для изучения реликтового излучения, которое возникло во время Большого взрыва (сейчас, после завершения миссии, отправлен на орбиту захоронения), космическая обсерватория Herschel, космическая обсерватория Планк, космический телескоп Gaia. В будущем сюда запустят один из самых важных проектов по изучению космоса — телескоп имени Джеймса Уэбби в 2024 году, который придет на смену культовому «Хабблу».

При этом все эти объекты, конечно же, находятся не в одной точке — а на гало-орбитах вокруг областей Лагранжа. Их достаточно много — несмотря на то, что зонды должны иметь стабилизирующее оборудование, позволяющее долго удерживаться на них.

Почему тогда на этих точках не собираются строить колонии?

Собираются. Есть несколько проектов по созданию колоний в точках Лагранжа, и есть даже общественные объединения, которые популяризируют эту идею — L5 Society, Republic of Lagrangia и National Space Society. Самым известным сторонником создания колонии-поселения человечества в точках Лагранжа считается астрофизик Джерард О’Нил, который представил концепцию «Острова III» — космической станции, находящейся в одной стабильной точке.

Однако у этих теорий есть несколько серьезных технических сложностей: негативное влияние солнечного ветра и других космических лучей на организм человека. Кроме того, все точки Лагранжа подвергаются пока слабо изученному воздействию плазмы в экваториальной плоскости магнитосферы Земли. В связи с этим все поселения, которые будут расположены в этих точках, должны быть защищены от космической радиации.

Кроме того, в связи с отсутствием гравитации постоянные космические поселения в точках Лагранжа должны быть оборудованы технологиями для создания ее искусственного аналога. При этом на сегодняшний день подобных технологий не существует.

Ну и самое главное. Пока все теории по созданию колоний на других планетах — гипотетические, для их появления человечеству необходимо сделать еще огромное количество открытий. Историю гонки создания баз на Луне и Марсе вы можете почитать здесь, здесь и здесь.

Ладно. Но я видел, что точки Лагранжа также могут быть использованы и для наблюдения инопланетянами за Землей!

Могут. В научной фантастике очень развита теория, что инопланетяне строят свои космические станции в точках, где нет гравитации, и наблюдают из них за Землей.

С одной стороны, некоторые точки Лагранжа, особенно в системе «Земля — Солнце», довольно сложно изучать, поскольку они находятся слишком близко к Солнцу (а иногда и за ним). Поэтому — теоретически — там могут находиться любые станции.

С другой стороны, эта теория остается только в научной фантастике, поскольку, как мы с вами давно знаем, существование инопланетян пока никем не доказано.

Источник

Журнал «Все о Космосе»

Точки Лагранжа

Точки Лагранжа и эквипотенциальные поверхности системы двух тел (с учётом центробежного потенциала)

Точки Лагранжа, точки либрации ( librātiō — раскачивание) или L-точки — точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, не испытывающее воздействие никаких других сил, кроме гравитационных, со стороны двух первых тел, может оставаться неподвижным относительно этих тел.

Более точно точки Лагранжа представляют собой частный случай при решении так называемой ограниченной задачи трёх тел — когда орбиты всех тел являются круговыми и масса одного из них намного меньше массы любого из двух других. В этом случае можно считать, что два массивных тела обращаются вокруг их общего центра масс с постоянной угловой скоростью. В пространстве вокруг них существуют пять точек, в которых третье тело с пренебрежимо малой массой может оставаться неподвижным во вращающейся системе отсчёта, связанной с массивными телами. В этих точках гравитационные силы, действующие на малое тело, уравновешиваются центробежной силой.

Точки Лагранжа получили своё название в честь математика Жозефа Луи Лагранжа, который первым в 1772 году привёл решение математической задачи, из которого следовало существование этих особых точек.

Расположение точек Лагранжа

Схема пяти лагранжевых точек в системе двух тел, когда одно тело намного массивнее другого (Солнце и Земля). В такой системе точки L3, L4, L5 показаны на самой орбите, хотя фактически они будут находиться немного за ней

Все точки Лагранжа лежат в плоскости орбит массивных тел и обозначаются заглавной латинской буквой L с числовым индексом от 1 до 5. Первые три точки расположены на линии, проходящей через оба массивных тела. Эти точки Лагранжа называются коллинеарными и обозначаются L₁, L₂ и L₃. Точки L₄ и L₅ называются треугольными или троянскими.

L₁ находится между двумя телами системы, ближе к менее массивному телу, L₂ — снаружи, за менее массивным телом и L₃ — за более массивным. Расстояния от центра масс системы до этих точек в первом приближении по α рассчитываются с помощью следующих формул:

,

R — расстояние между телами, M₁ — масса более массивного тела, M₂ — масса второго тела.

Точка L₁ лежит на прямой, соединяющей два тела с массами M₁ и M₂ (M₁ > M₂), и находится между ними, вблизи второго тела. Её наличие обусловлено тем, что гравитация тела M₂ частично компенсирует гравитацию тела M₁. При этом чем больше M₂, тем дальше от него будет располагаться эта точка.

Пример: Объекты, которые движутся вокруг Солнца ближе, чем Земля, как правило, имеют меньшие орбитальные периоды, чем у Земли, если они не входят в зону влияния земного притяжения. Если объект находится непосредственно между Землёй и Солнцем, то действие земной силы тяжести отчасти компенсирует влияние гравитации Солнца, за счёт этого происходит увеличение орбитального периода объекта. Причём чем ближе к Земле находится объект, тем сильнее этот эффект. И наконец, на определённом приближении к планете — в точке L₁ — действие земной силы тяжести уравновешивает влияние солнечной гравитации настолько, что период обращения объекта вокруг Солнца становится равным периоду обращения Земли. Для нашей планеты расстояние до точки L₁ составляет около 1,5 млн км. Притяжение Солнца здесь (118 мкм/с²) на 2 % сильнее, чем на орбите Земли (116 мкм/с²), тогда как снижение требуемой центростремительной силы вдвое меньше (59 мкм/с²). Сумма этих двух эффектов уравновешивается притяжением Земли, которое составляет здесь также 177 мкм/с². Использование

В системе Солнце—Земля точка L₁ может быть идеальным местом для размещения космической обсерватории для наблюдения Солнца, которое в этом месте никогда не перекрывается ни Землёй, ни Луной. Первым космическим аппаратом, работавшим вблизи этой точки, был запущенный в августе 1978 года аппарат ISEE-3 . Аппарат вышел на периодическую гало-орбиту вокруг этой точки 20 ноября 1978 года и был сведён с этой орбиты 10 июня 1982 года (для исполнения новых задач). На такой же орбите с мая 1996 года работает аппарат SOHO. Аппараты ACE, WIND и DSCOVR находятся на квази-периодических орбитах Лиссажу́ близ этой же точки, соответственно, с 12 декабря 1997, 16 ноября 2001 и 8 июня 2015 года.

Лунная точка L₁ (в системе Земля — Луна) может стать идеальным местом для строительства космической пилотируемой орбитальной станции, которая, располагаясь на «полпути» между Землёй и Луной, позволила бы легко добраться до Луны с минимальными затратами топлива и стать ключевым узлом грузового потока между Землёй и её спутником.

Точка L2 в системе Солнце — Земля, располагающаяся далеко за пределами орбиты Луны

Точка L₂ лежит на прямой, соединяющей два тела с массами M₁ и M₂ (M₁ > M₂), и находится за телом с меньшей массой. Точки L₁ и L₂ располагаются на одной линии и в пределе M₁ ≫ M₂ симметричны относительно M₂. В точке L₂гравитационные силы, действующие на тело, компенсируют действие центробежных сил во вращающейся системе отсчёта.

Пример: у объектов, расположенных за орбитой Земли, орбитальный период почти всегда больше, чем у Земли. Но дополнительное влияние на объект силы тяжести Земли, помимо действия солнечной гравитации, приводит к увеличению скорости вращения и уменьшению времени оборота вокруг Солнца, в результате в точке L₂орбитальный период объекта становится равным орбитальному периоду Земли.

Точка L₂ в системе Солнце — Земля является идеальным местом для строительства орбитальных космических обсерваторий и телескопов. Поскольку объект в точке L₂ способен длительное время сохранять свою ориентацию относительно Солнца и Земли, производить его экранирование и калибровку становится гораздо проще. Однако эта точка расположена немного дальше земной тени (в области полутени), так что солнечная радиация блокируется не полностью. В этой точке уже находятся аппараты американского и европейского космических агентств — WMAP, «Планк», «Гершель» и “Gaia”, а в 2018 должен присоединиться «Джеймс Уэбб». Точка L₂ в системе Земля—Луна может быть использована для обеспечения спутниковой связи с объектами на обратной стороне Луны, а также быть удобным местом для размещения заправочной станции для обеспечения грузопотока между Землёй и Луной .

Если M₂ много меньше по массе, чем M₁, то точки L₁ и L₂ находятся на примерно одинаковом расстоянии r от тела M₂, равном радиусу сферы Хилла :

где R — расстояние между компонентами системы.

Это расстояние можно описать как радиус круговой орбиты вокруг M₂, для которой период обращения в отсутствие M₁ в раз меньше, чем период обращения M₂ вокруг M₁.

Примеры

• В системе Солнце — Земля: 1 500 000 км от Земли
• Земля — Луна: 61 500 км от Луны

Три из пяти точек Лагранжа расположены на одной оси, соединяющей два тела

Точка L₃ лежит на прямой, соединяющей два тела с массами M₁ и M₂ (M₁ > M₂), и находится за телом с большей массой. Так же, как для точки L₂, в этой точке гравитационные силы компенсируют действие центробежных сил.

Пример: Точка L₃ в системе Солнце — Земля находится за Солнцем, на противоположной стороне земной орбиты. Однако, несмотря на свою небольшую гравитацию (по сравнению с гравитацией Солнца), Земля всё же оказывает на него небольшое влияние, поэтому точка L₃ находится не на самой орбите Земли, а чуть дальше от Солнца, чем Земля, так как вращение происходит не вокруг Солнца, а вокруг барицентра). В результате в этой точке L₃ достигается такое сочетание гравитации Солнца и Земли, что объекты, находящиеся в этой точке, движутся с таким же орбитальным периодом, как и наша планета.

До начала космической эры среди писателей-фантастов была очень популярна идея о существовании на противоположной стороне земной орбиты в точке L₃ другой аналогичной ей планеты, называемой «Противоземлёй», которая из-за своего расположения была недоступна для прямых наблюдений. Однако на самом деле из-за гравитационного влияния других планет точка L₃ в системе Солнце — Земля является крайне неустойчивой. Так, во время гелиоцентрических соединений Земли и Венеры по разные стороны Солнца, которые случаются каждые 20 месяцев, Венера находится всего в 0,3 а. е. от точки L₃ и таким образом оказывает очень серьёзное влияние на её расположение относительно земной орбиты. Кроме того, из-за несбалансированности центра тяжести системы Солнце — Юпитер относительно Земли и эллиптичности земной орбиты, так называемая «Противоземля» всё равно время от времени была бы доступна для наблюдений и обязательно была бы замечена. Ещё одним эффектом, выдающим её существование, была бы её собственная гравитация: влияние тела размером уже порядка 150 км и более на орбиты других планет было бы заметно. С появлением возможности производить наблюдения с помощью космических аппаратов и зондов было достоверно показано, что в этой точке нет объектов размером более 100 м.

Орбитальные космические аппараты и спутники, расположенные вблизи точки L₃, могут постоянно следить за различными формами активности на поверхности Солнца, в частности, о появлении новых пятен или вспышек, и оперативно передавать информацию на Землю (например, в рамках системы раннего предупреждения о космической погоде NOAA Space Weather Prediction Center ). Кроме того, информация с таких спутников может быть использована для обеспечения безопасности дальних пилотируемых полётов, например к Марсу или астероидам. В 2010 году были изучены несколько вариантов запуска подобного спутника .

L₄ и L₅

Гравитационное ускорение в точке L4

Если на основе линии, соединяющей оба тела системы, построить два равносторонних треугольника, две вершины которых соответствуют центрам тел M₁ и M₂, то точки L₄ и L₅ будут соответствовать положению третьих вершин этих треугольников, расположенных в плоскости орбиты второго тела в 60 градусах впереди и позади него.

Наличие этих точек и их высокая стабильность обусловливается тем, что, поскольку расстояния до двух тел в этих точках одинаковы, то силы притяжения со стороны двух массивных тел соотносятся в той же пропорции, что их массы, и таким образом результирующая сила направлена на центр масс системы; кроме того, геометрия треугольника сил подтверждает, что результирующее ускорение связано с расстоянием до центра масс той же пропорцией, что и для двух массивных тел. Так как центр масс является одновременно и центром вращения системы, результирующая сила точно соответствует той, которая нужна для удержания тела в точке Лагранжа в орбитальном равновесии с остальной системой. (На самом деле, масса третьего тела и не должна быть пренебрежимо малой). Данная треугольная конфигурация была обнаружена Лагранжем во время работы над задачей трёх тел. Точки L₄ и L₅ называют треугольными (в отличие от коллинеарных).

Также точки называют троянскими: это название происходит от троянских астероидов Юпитера, которые являются самым ярким примером проявления этих точек. Они были названы в честь героев Троянской войны из «Илиады» Гомера, причём астероиды в точке L₄ получают имена греков, а в точке L₅ — защитников Трои; поэтому их теперь так и называют «греками» (или «ахейцами») и «троянцами».

Расстояния от центра масс системы до этих точек в координатной системе с центром координат в центре масс системы рассчитываются по следующим формулам:

, R — расстояние между телами, M₁ — масса более массивного тела, M₂ — масса второго тела.

Примеры

• В 2010 году в системе Солнце — Земля в троянской точке L₄ обнаружен астероид. В L₅ пока не обнаружено троянских астероидов, но там наблюдается довольно большое скопление межпланетной пыли.
• По некоторым наблюдениям, в точках L₄ и L₅ системы Земля — Луна находятся очень разрежённые скопления межпланетной пыли — облака Кордылевского.
• В системе Солнце — Юпитер в окрестностях точек L₄ и L₅ находятся так называемые троянские астероиды. По состоянию на 21 октября 2010 известно около четырёх с половиной тысяч астероидов в точках L₄ и L₅.
• Троянские астероиды в точках L₄ и L₅ есть не только у Юпитера, но и у других планет-гигантов.
• Другим интересным примером является спутник СатурнаТефия, в точках L₄ и L₅ которой находятся два небольших спутника — Телесто и Калипсо. Ещё одна пара спутников известна в системе Сатурн — Диона: Елена в точке L₄ и Полидевк в точке L₅. Тефия и Диона в сотни раз массивнее своих «подопечных», и гораздо легче Сатурна, что делает систему стабильной.
• Один из сценариев модели ударного формирования Луны предполагает, что гипотетическая протопланета (планетезималь) Тейя, в результате столкновения которой с Землёй образовалась Луна, сформировалась в точке Лагранжа L₄ или L₅ системы Солнце — Земля.
• Первоначально считалось, что в системе KOI-730 две из четырёх планет обращаются вокруг своего солнца по одной орбите. Вдоль общей орбиты эти два мира постоянно разделяют 60 градусов дистанции. Однако дальнейшие исследования показали, что данная система не содержит коорбитальных планет.

Равновесие в точках Лагранжа

Изображение двойной звезды Мира (омикрон Кита), сделанное космическим телескопом «Хаббл» в ультрафиолетовом диапазоне. На фотографии виден поток материи, направленный от основного компонента — красного гиганта — к компаньону — белому карлику. Массообмен осуществляется через окрестности точки L1

Тела, помещённые в коллинеарных точках Лагранжа, находятся в неустойчивом равновесии. Например, если объект в точке L₁ слегка смещается вдоль прямой, соединяющей два массивных тела, сила, притягивающая его к тому телу, к которому оно приближается, увеличивается, а сила притяжения со стороны другого тела, наоборот, уменьшается. В результате объект будет всё больше удаляться от положения равновесия.

Такая особенность поведения тел в окрестностях точки L₁ играет важную роль в тесных двойных звёздных системах. Полости Роша компонент таких систем соприкасаются в точке L₁, поэтому, когда одна из звёзд-компаньонов в процессе эволюции заполняет свою полость Роша, вещество перетекает с одной звезды на другую именно через окрестности точки Лагранжа L₁.

Несмотря на это, существуют стабильные замкнутые орбиты (во вращающейся системе координат) вокруг коллинеарных точек либрации, по крайней мере, в случае задачи трёх тел. Если на движение влияют и другие тела (как это происходит в Солнечной системе), вместо замкнутых орбит объект будет двигаться по квазипериодическим орбитам, имеющим форму фигур Лиссажу. Несмотря на неустойчивость такой орбиты, космический аппарат может оставаться на ней в течение длительного времени, затрачивая относительно небольшое количество топлива.

В отличие от коллинеарных точек либрации, в троянских точках обеспечивается устойчивое равновесие, если M₁/M₂ > 24,96 . При смещении объекта возникают силы Кориолиса, которые искривляют траекторию, и объект движется по устойчивой орбите вокруг точки либрации.

Практическое применение

Полости Роша для двойной звёздной системы (обозначены жёлтым)

Исследователи в области космонавтики давно уже обратили внимание на точки Лагранжа. Например, в точке L₁ системы Земля — Солнце удобно разместить космическую солнечную обсерваторию — она никогда не будет попадать в тень Земли, а значит, наблюдения могут вестись непрерывно. Точка L₂ подходит для космического телескопа — здесь Земля почти полностью заслоняет солнечный свет, да и сама не мешает наблюдениям, поскольку обращена к L₂ неосвещенной стороной. Точка L₁ системы Земля — Луна удобна для размещения ретрансляционной станции в период освоения Луны. Она будет находиться в зоне прямой видимости для большей части обращённого к Земле полушария Луны, а для связи с ней понадобятся передатчики в десятки раз менее мощные, чем для связи с Землёй.

В настоящее время несколько космических аппаратов, в первую очередь, астрофизических обсерваторий, размещены или планируются к размещению в различных точках Лагранжа Солнечной системы:

Точка L₁ системы Земля—Солнце:

• Космический аппарат WIND, предназначенный для исследования солнечного ветра (запущен в 1994 году).
• SOHO ( Solar and Heliospheric Observatory , «Солнечная и гелиосферная обсерватория») (запущен в 1995 году).
• Advanced Composition Explorer (запущен в 1997 году).

Точка L₂ системы Земля—Солнце:

• КА НАСА WMAP, изучающий реликтовое излучение (запущен в 2001 году).
• Космические телескопы «Гершель» и «Планк», (запущены в 2009 году).
• Европейский телескоп «Gaia» (запущен в 2013 году).
• Космический телескоп «Джеймс Уэбб», идущий на смену телескопу «Хаббл». Запуск планируется на 2018 год.
• В 2017 году НПО имени Лавочкина планирует разместить в точке L₂ космическую обсерваторию Спектр-РГ.
• В 2024 году ЕКА планирует также разместить в точке L₂ космический телескоп «PLATO».

Другие точки Лагранжа:

• в сентябре-октябре 2009 года два аппарата STEREO совершили транзит через точки L₄ и L₅.
• JIMO ( Jupiter Icy Moons Orbiter ) — отменённый проект НАСА по исследованию спутников Юпитера, который должен был активно использовать систему точек Лагранжа для перехода от одного спутника к другому с минимальными затратами топлива. Этот манёвр получил название «лестница Лагранжа».

Источник