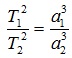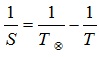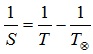Таблица планета эксцентриситет среднее расстояние до солнца сидерический период

a Отношение массы Солнца к массе планеты (включая атмосферу и массу спутников).
b Без учета массы спутников.
c Сжатие равно (Re-Rp)/Re, где Re и Rp — экваториальный и полярный радиусы планет (соответственно).
d Значения в скобках могут отличаться более чем на 10 процентов.
e По решению МАС, северный полюс любой планеты направлен к северу от эклиптической плоскости, поэтому Венера, Уран и Плутон имеют обратное направление вращения.
f Для внешних планет не имеющих твердой поверхности радиус соответствует уровню атмосферного давления в 1 бар..
g Период вращения Юпитера (Система III) — 9.925 часов.
h Период вращения Сатурна — 10.675 часов.
i Период вращения Урана — 17.240 часов.
j Период вращения Нептуна — 16.11 часов.

Характеристики планетарных орбит

Среднее расстояние от Солнца
(а.е.)	(10 6 км)

Сидерический период
(годы)	(дни)

Синодический период (дни)

Средняя орбитальная скорость (км/с)

Эксцентриситет орбиты

Накло-
нение эклиптики (градусы)

МЕРКУРИЙ

0.3871

57.91

0.24085

87.969

115.88

47.89

0.2056

7.004

ВЕНЕРА

0.7233

108.20

0.61521

224.701

583.92

35.03

0.0068

3.394

ЗЕМЛЯ

1.0000

149.60

1.00004

365.256

—

29.79

0.0167

0.000

МАРС

1.5237

227.94

1.88089

686.980

779.94

24.13

0.0934

1.850

ЮПИТЕР

5.2028

778.33

11.8623

4,332.71

398.88

13.06

0.0483

1.308

САТУРН

9.5388

1,426.98

29.458

10,759.5

378.09

9.64

0.0560

2.488

УРАН

19.1914

2,870.99

84.01

30,685

369.66

6.81

0.0461

0.774

НЕПТУН

30.0611

4,497.07

164.79

60,190

367.49

5.43

0.0097

1.774

ПЛУТОН

39.5294

5,913.52

248.54

90,800

366.73

4.74

0.2482

17.148

Данные таблицы приведены с разрешения The New solar System (3rd edition), edited by J. Kelly Beatty and Andrew Chaikin, Cambridge University Press and Sky Publishing Corp., 1990 © Sky Publishing Corp.

Источник

Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера

вкл. 27 Ноябрь 2016 .

Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера

1. Сформулируйте законы Кеплера.

Первый закон Кеплера	Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце
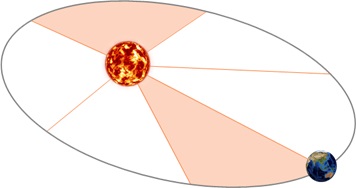
Второй закон Кеплера	Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади
Третий закон Кеплера	Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит

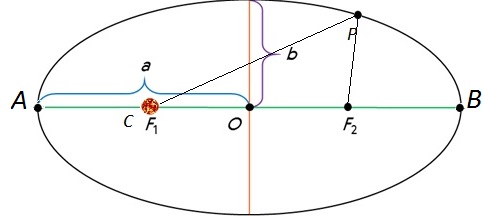
2. На рисунке 8.1 укажите точки афелия и перигелия.

3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.

Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).

4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.

5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.

6. Выполните задание.

1. На рисунке 8.1, а укажите точки орбиты, в которых:

а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.

2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)

1. На рисунке 8.1, б укажите точки орбиты, в которых:

а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.

2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)

7. Решите задачи.

1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.

2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?

1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.

2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?

Источник

Таблица планета эксцентриситет среднее расстояние до солнца сидерический период

Рассмотрите таблицу, содержащую сведения о планетах земной группы Солнечной системы.

Параметры	Меркурий	Венера	Земля	Марс
Среднее расстояние до Солнца (а. е.)	0,4	0,7	1,0	1,5
Радиус (в радиусах Земли)	0,38	0,95	1	0,53
Масса (в массах Земли)	0,055	0,815	1	0,108
Период вращения вокруг оси	59 сут.	243 сут.	24 ч	24,6 ч
Период обращения вокруг Солнца	88 сут.	225 сут.	365 сут.	687 сут.
Эксцентриситет орбиты	0,206	0,007	0,017	0,093
Количество спутников	0	0	1	2

Выберите два утверждения, которые соответствуют характеристикам планет, и укажите их номера.

1) Из планет земной группы по наиболее вытянутой орбите вокруг Солнца вращается Венера.

2) Ускорение свободного падения на Марсе равно примерно 3,8 м/с 2 .

3) Первая космическая скорость для Меркурия меньше, чем для Земли.

4) Среди планет земной группы частота обращения вокруг Солнца максимальная у Венеры.

5) Средняя плотность Меркурия меньше, чем у Венеры.

1. Наиболее вытянутая орбита имеет наибольший эксцентриситет. По таблице видно, что наибольший эксцентриситет орбиты (0,206) у Меркурия, а не у Венеры. Утверждение 1 ошибочно.

2. Ускорение свободного падения на планете можно найти по формуле

[math]g=G\times\\frac M[/math] где G = 6,7 • 10 -11 Н • м 2 /кг 2 — гравитационная постоянная, М — масса планеты, R — её радиус.

Следовательно, ускорение свободного падения на Марсе g_м = 10 x 0,38 = 3,8 м/с 2 . Утверждение 5 верное.

3. Как известно из курса механики, первой космической скоростью называется минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите. Она вычисляется по формуле

Следовательно, ускорение свободного падения для Меркурия меньше, чем для Земли. Третье утверждение справедливо.

4. Частота вращения обратно пропорциональна периоду. Соответственно, максимальная частота соответствует самому маленькому периоду. Из таблицы видно, что такой период имеет не Венера, а Меркурий. Утверждение 4 ошибочно.

5. Средняя плотность планеты равна отношению массы планеты к её

Плотность Меркурия больше плотности Венеры. Утверждение 5 ошибочно.

Предложи свой вариант решения в комментариях 👇🏻

Источник

ИНФОФИЗ — мой мир.

Весь мир в твоих руках — все будет так, как ты захочешь

Как сказал.

Есть только два способа прожить жизнь. Первый — будто чудес не существует. Второй — будто кругом одни чудеса.

А.Эйнштейн

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»

Тема: Законы Кеплера. Определение масс небесных тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

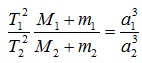
где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ — соответственно массы их спутников.

Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

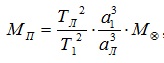
где Т_л и α _л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

б) для внутренней планеты:

Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Источник