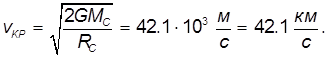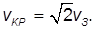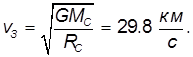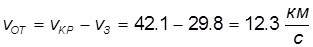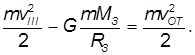Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
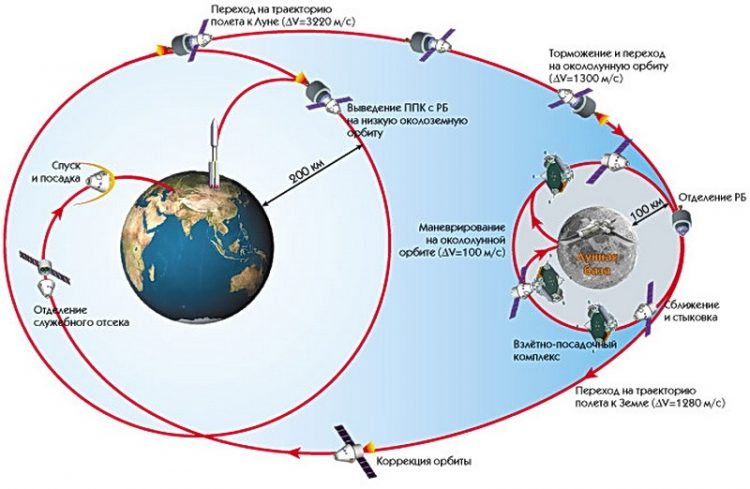
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
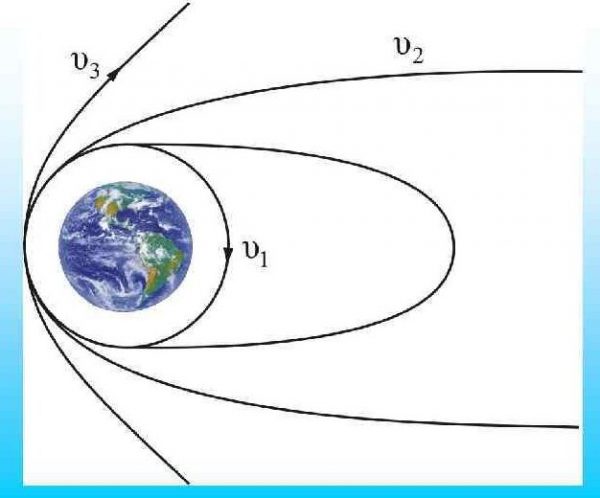
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
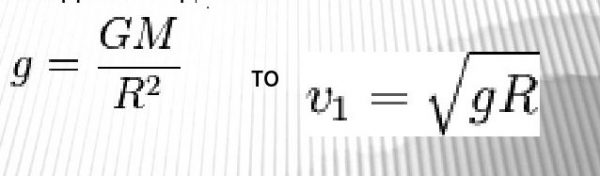
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
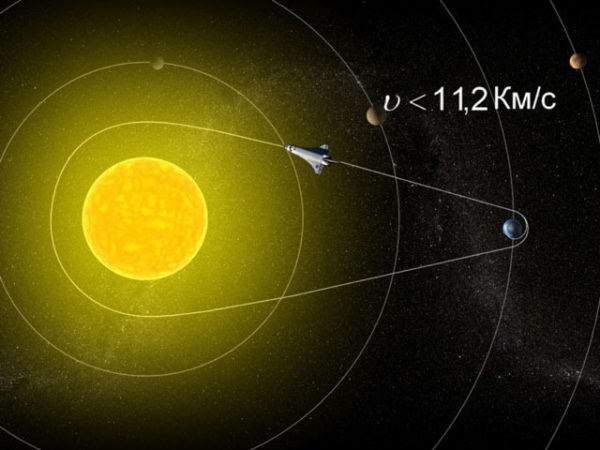
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник
5.6. Космические скорости
Применим закон всемирного тяготения для определения двух характерных «космических» скоростей, связанных с размерами и полем тяготения некоторой планеты. Планету будем считать одним шаром.
Рис. 5.8. Различные траектории движения спутников вокруг Земли
Первой космической скоростью 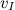
Это, конечно идеализация, во-первых планета не шар, во-вторых, если у планеты есть достаточно плотная атмосфера, то такой спутник — даже если его удастся запустить — очень быстро сгорит. Другое дело, что, скажем спутник Земли, летающий в ионосфере на средней высоте над поверхностью в 200 км имеет радиус орбиты отличающийся от среднего радиуса Земли всего, примерно, на 3 %.
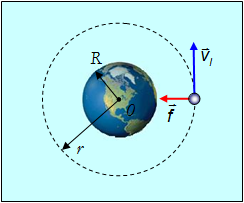
На спутник, движущийся по круговой орбите радиусом 
Рис. 5.9. Движение искусственного спутника Земли по круговой орбите
По второму закону Ньютона имеем
Если спутник движется недалеко от поверхности Земли, то
Поэтому для 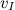
Видно ,что 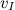
Период обращения спутника вокруг Земли равен
где 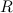

Минимальное значение периода обращения достигается при движении по орбите, радиус которой равен радиусу планеты:
так что первую космическую скорость можно определить и так: скорость спутника на круговой орбите с минимальным периодом обращения вокруг планеты.
Период обращения растет с увеличением радиуса орбиты.
Если период обращения спутника равен периоду обращения Земли вокруг своей оси и их направления вращения совпадают, а орбита расположена в экваториальной плоскости, то такой спутник называется геостационарным.
Геостационарный спутник постоянно висит над одной и той же точкой поверхности Земли (рис. 5.10).
Рис. 5.10. Движение геостационарного спутника
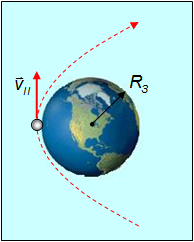
Для того чтобы тело могло выйти из сферы земного притяжения, то есть могло удалиться на такое расстояние, где притяжение к Земле перестает играть существенную роль, необходима вторая космическая скорость (рис. 5.11).
Второй космической скоростью 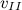
Рис. 5.11. Вторая космическая скорость
Для того чтобы тело (при отсутствии сопротивления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы кинетическая энергия тела на поверхности планеты была равна (или превосходила) работу, совершаемую против сил земного притяжения. Напишем закон сохранения механической энергии Е такого тела. На поверхности планеты, конкретно — Земли
Скорость 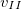
Приравнивая эти два выражения,получаем
откуда для второй космической скорости имеем
Для сообщения запускаемому объекту необходимой скорости (первой или второй космической) выгодно использовать линейную скорость вращения Земли, то есть запускать его как можно ближе к экватору, где эта скорость составляет, как мы видели, 463 м/с (точнее 465,10 м/с). При этом направление запуска должно совпадать с направлением вращения Земли — с запада на восток. Легко подсчитать, что таким способом можно выиграть несколько процентов в энергетических затратах.
В зависимости от начальной скорости 
- если
, то тело упадет на Землю.
- если
, то тело будет двигаться по эллиптической траектории.
- если
, то тело «уйдет на бесконечность» по парабалической траектории
- если
, то тело «уйдет на бесконечность» по гиперболической траектории.
Рис. 5.12. Формы траектории частицы в зависимости от скорости бросания
Совершенно аналогично рассчитывается движение в гравитационном поле любого другого космического тела,например, Солнца. Чтобы преодолеть силу притяжения светила и покинуть Солнечную систему,объекту,покоящемусю относительно Солнца и находящемуся от него на расстоянии, равном радиусу земной орбиты 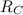
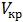
где 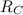
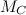
Отсюда следует формула, аналогичная выражению для второй космической скорости, где надо заменить массу Земли на массу Солнца и радиус Земли на радиус земной орбиты:
Подчеркнем, что 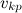
Отметим также связь
с орбитальной скоростью Земли 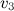
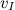
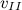
На практике мы запускаем ракету с Земли, так что она заведомо участвует в орбитальном движении вокруг Солнца. Как было показано выше, Земля движется вокруг Солнца с линейной скоростью
Ракету целесообразно запускать в направлении движения Земли вокруг Солнца.
Скорость, которую необходимо сообщить телу на Земле, чтобы оно навсегда покинуло пределы Солнечной системы, называется третьей космической скоростью 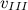
Скорость 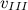
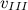
Понять происхождение этого числа можно также из энергетических соображений. Казалось бы, достаточно ракете сообщить относительно Земли скорость
в направлении движения Земли вокруг Солнца, и она покинет пределы Солнечной системы. Но это было бы правильно, если бы Земля не имела собственного поля тяготения. Такую скорость тело должно иметь, уже удалившись из сферы земного притяжения. Поэтому подсчет третьей космической скорости очень похож на вычисление второй космической скорости, но с дополнительным условием — тело на большом расстоянии от Земли должно все еще иметь скорость 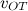
В этом уравнении мы можем выразить потенциальную энергию тела на поверхности Земли (второе слагаемое в левой части уравнения) через вторую космическую скорость 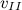
Источник


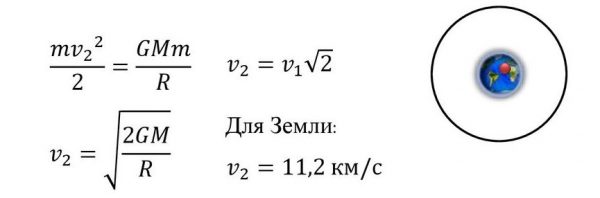

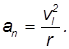

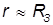
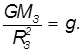
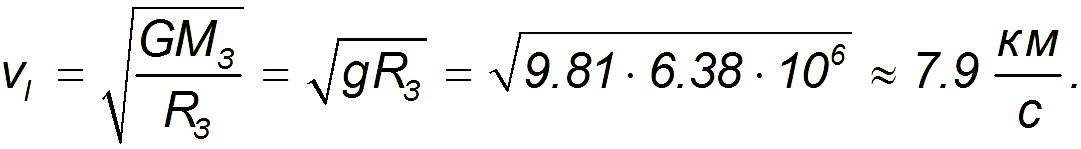
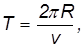
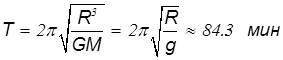
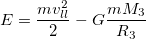
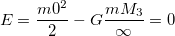
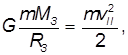
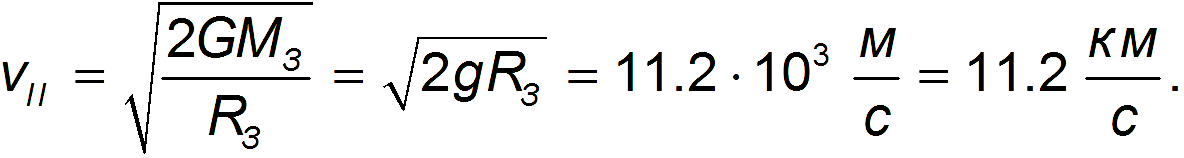
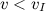 , то тело упадет на Землю.
, то тело упадет на Землю.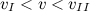 , то тело будет двигаться по эллиптической траектории.
, то тело будет двигаться по эллиптической траектории.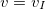 , то тело «уйдет на бесконечность» по парабалической траектории
, то тело «уйдет на бесконечность» по парабалической траектории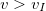 , то тело «уйдет на бесконечность» по гиперболической траектории.
, то тело «уйдет на бесконечность» по гиперболической траектории.