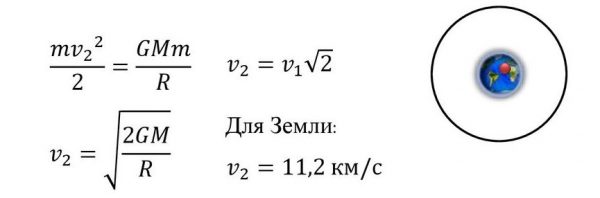Скорость движения планет вокруг солнца первая космическая

В начале XVI века польским астрономом Н. Коперником (1473–1543) обоснована гелиоцентрическая система, согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория наблюдения Коперника воспринималась как занимательная фантазия. В XVI в. это утверждение рассматривалось церковью как ересь. Известно, что Дж. Бруно, открыто выступивший в поддержку гелиоцентрической системы Коперника, был осужден инквизицией и сожжен на костре.

Однако к началу XVII столетия большинство ученых убедились в справедливости гелиоцентрической системы мира. Иоганн Кеплер, обработав результаты многочисленных наблюдений, проведенных Тихо Браге (которого называют «человеком, измерившим небо»), получил законы движения планет вокруг Солнца. Кеплер Иоганн (1571–1630) – немецкий ученый, один из творцов небесной механики. Работы в области астрономии, механики, математики. Используя наблюдения Тихо Браге и свои собственные, открыл законы движения планет (три закона Кеплера). Известен как конструктор телескопа (так называемая зрительная труба Кеплера, состоящая из двух двояковыпуклых линз).

Закон всемирного тяготения был открыт Ньютоном на основе трех законов Кеплера.

Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце (рис. 7.6).

Рис. 7.7

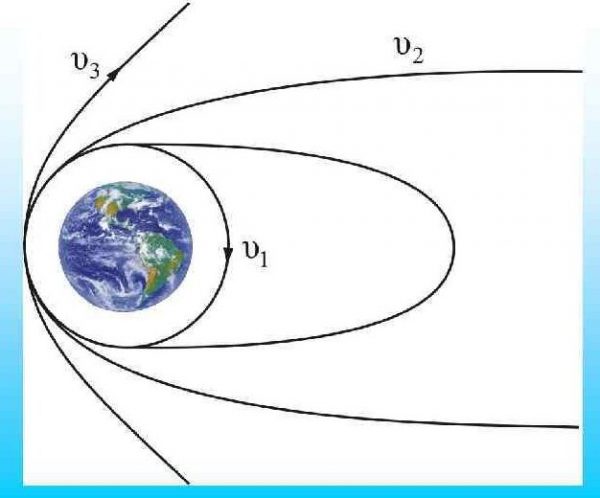
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит.

R 3 (Т – период обращения; R – радиус орбиты).

Ньютон решил обратную задачу механики и из законов движения планет получил выражение для гравитационной силы:

Потенциальная энергия тела массы m, расположенного на расстоянии r от большого тела массы М, есть

Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна:

Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела.

На рисунке 7.8, показаны траектории тел с различными космическими скоростями.

Источник

Космические скорости

Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?

На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.

Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.

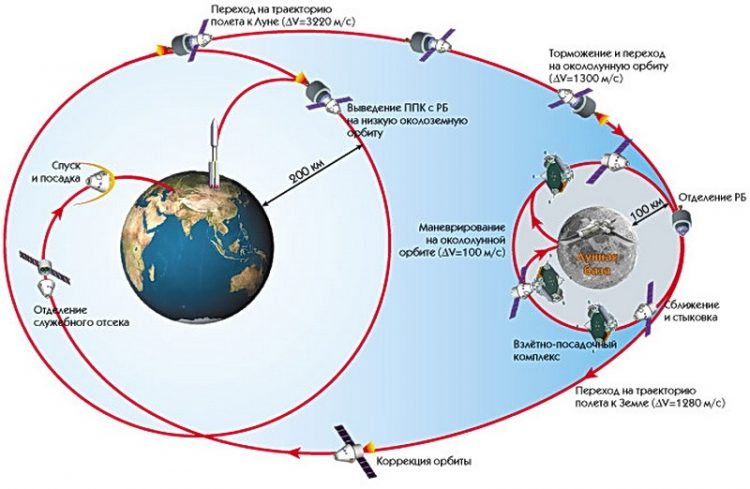
Траектория полета космических кораблей

Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.

Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.

Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:

• v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
• v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
• v3 — покинуть при запуске планету, преодолев притяжение Звезды;
• v4 — при запуске из планетной системы объект покинул Галактику.

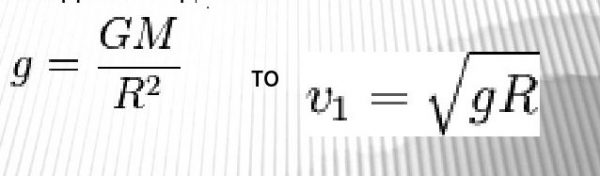
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.

Первая космическая скорость

Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.

Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

Формула

где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем

7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения —

Вторая космическая скорость

Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.

Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:

• для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
• для Солнца вторая космическая скорость составляет 617,7 км/с.
• для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.

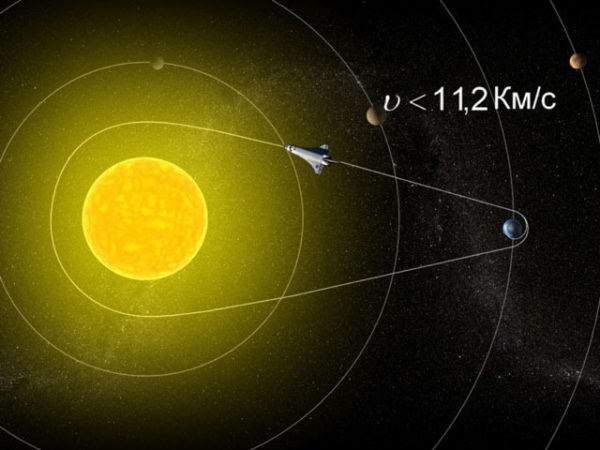
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.

Формула

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .

Третья космическая скорость

Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.

Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.

Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.

Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.

При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.

Четвёртая и пятая космическая скорости

Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.

Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.

Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.

По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.

Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.

Видео

Источник

Первая космическая скорость

Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.

То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно \( R = \left( r + h \right) \). Это представлено на рисунке 1.

Формула для вычисления первой космической скорости

Первую космическую скорость можно посчитать по формуле:

\( v \left( \frac<\text<м>><\text> \right) \) (метры в секунду) – первая космическая скорость

\( M \left( \text <кг>\right) \) (килограммы) — масса планеты, вокруг которой движется спутник

\( r \left( \text <м>\right) \) (метры) – радиус планеты

\( h \left( \text <м>\right) \) (метры) — расстояние от поверхности планеты до спутника

\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная

Первая космическая скорость в цифрах для некоторых небесных тел

первая космическая скорость у поверхности Земли \( v = 8000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Солнца \( v = 437000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Луны \( v = 1680 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Марса \( v = 3530 \left( \frac<\text<м>><\text> \right) \)

Как выводится формула первой космической скорости

Рассмотрим движение спутника вокруг Земли.

Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником

При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).

Мы можем записать эти уравнения в виде системы.

\[ \begin \displaystyle F = G\cdot \frac <(r+h)^<2>> \\ \displaystyle F_<\text<ц>> = m \cdot \frac > <(r+h)>\\ \end \]

Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:

А если равны левые части уравнений, то будут равны и правые:

Масса \( m \) спутника и расстояние \( R \) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.

Теперь умножим обе части уравнения на расстояние \(\left( r + h \right) \). Получим:

Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:

Вам будет интересно почитать:

Движение по окружности, центростремительная сила и центростремительное ускорение

Источник