Скорость для достижения луны

Скорость для достижения луны

Скорость полета к Луне

Вопроса о скоростях полета к Луне и, в частности, о минимальной скорости мы уже отчасти касались, когда речь шла о точках либрации системы Земля — Луна. Для первой критической скорости (т. е. наименьшей скорости отлета от Земли, которая в принципе обеспечивает возможность достижения Луны) при старте с орбиты спутника Земли с высотой 200 км, плоскость которой совпадает с плоскостью орбиты движения Луны, было получено значение 10,84890 км/сек. Поскольку скорость полета по такой орбите спутника Земли составляет 7,791 км/сек, то для достижения первой критической скорости потребуется доразгон на величину 3,058 км/сек.

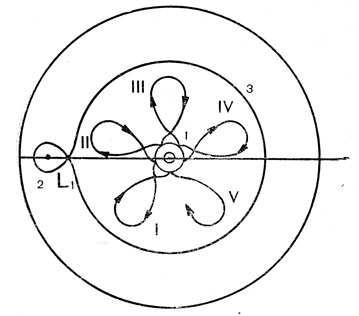
Рис. 76. Первые обороты с минимальной критической начальной скоростью во вращающихся координатах: 1 — Земля; 2 — Луна; 3 — линия Хилла; I, II, III, IV, V — номера витков

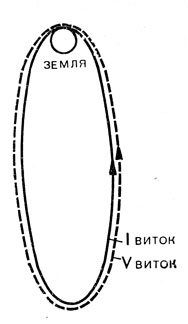
Рис. 77. Предыдущая траектория в невращающейся системе координат

Рассмотрим теперь особенности движения космического аппарата. Проекция траектории полета его при старте с первой критической скоростью во вращающейся вместе с Луной и Землей системой координат на плоскость орбиты Луны показаны на рис. 76. На нем же изображена линия Хилла в виде несимметричной восьмерки, соответствующая указанным условиям старта. Напомним, что линия Хилла определяет границу допустимых движений космического аппарата. Она, в частности, показывает, что достижение Луны может произойти только при пролете космического аппарата через узкую «лазейку», совпадающую с точкой либрации L₁. Расчет траектории полета производился методом численного интегрирования уравнений движения. Результаты расчетов показывают, что при отлете от Земли с первой критической скоростью траектория космического аппарата возвращается к Земле, не доходя до линии Хилла примерно на 30000 км. Орбита космического аппарата на первых витках по форме очень близка к эллипсу с радиусом апогея около 260 тыс. км (рис. 77). Однако от витка к витку высота апогея постепенно возрастает, но темп возрастания ее является очень малым. Для приведенных на рис. 76 пяти оборотов космического аппарата в выбранном масштабе отметить увеличение высоты апогея просто невозможно. Пройдет, следовательно, очень много времени, пока он достигнет линии Хилла. Но это не все: ведь для прилета к Луне необходимо, чтобы космический аппарат достиг линии Хилла в точке L₁, и только после этого он может перейти в левую часть восьмерки, т. е. оказаться в районе Луны. Таким образом, полет к Луне с минимальной скоростью практически оказывается невозможным, поскольку перед его осуществлением космический аппарат должен сделать достаточно большое число оборотов вокруг Земли. Оценочные расчеты, выполненные В. А. Егоровым, показывают, что для достижения линии Хилла космический аппарат должен совершить порядка 200 оборотов, затратив на это 1200 суток. Это объясняется тем, что влияние Луны оказывается относительно небольшим.

Аналогичные расчеты для старта с Земли со второй (10,84968 км/сек), с третьей (10,85738 км/сек) и с четвертой (10,85854 км/сек) критическими скоростями показывают, что здесь также не удается достичь Луны на первом обороте. Следовательно, полет к Луне с такими скоростями также не целесообразен. Вот по, этой причине приходится искать другой подход к задаче выбора скорости полета к Луне.

Мы уже убедились, что на первом обороте движения с минимальными скоростями орбита полета космического аппарата по своей форме очень близка к эллипсу с фокусом в центре Земли и ее можно приближенно (но с хорошей точностью) рассчитывать по эллиптической теории, т. е. без учета притяжения Луны. Это обстоятельство наводит на мысль найти минимальные скорости на первом обороте приближенно, полностью пренебрегая влиянием Луны. Минимальная геоцентрическая начальная скорость, как нетрудно догадаться, должна быть выбрана так, чтобы высота апогея эллипса сравнялась с расстоянием до Луны. При строго вертикальном старте с поверхности Земли эта скорость будет равна 10,90525 км/сек. При старте с орбиты спутника Земли с высотой 200 км она возрастает всего лишь на 1,6 м/сек. Для сравнения укажем, что вторая космическая (параболическая) скорость в этом случае составляет 10,99967 км/сек и, следовательно, минимальная скорость полета к Луне меньше ее всего на 92,828 м/сек. Таким образом, увеличив минимальную скорость полета к Луне всего на 93 м/сек, космический аппарат навсегда покинет Землю и превратится в искусственную планету, вращающуюся вокруг Солнца.

Pис. 78. Возмущение Луной эллипса, достигающего точки равенства притяжений Земли и Луны: 1 — орбита без притяжения Луны; 2 — орбита с притяжением Луны. Точками на орбите обозначено время полета в сутках

Траектория, соответствующая минимальной скорости отлета от Земли, показана на рис. 77. Эти расчеты подтверждают, что выбранное нами условие нахождения минимальной скорости (равенство высоты апогея эллипса расстоянию до Луны) является достаточным для обеспечения попадания в Луну с высокой точностью. Более строгий анализ этого вопроса показывает, что найденную из этого условия скорость полета к Луне необходимо уменьшить на 2 см/сек, что является, конечно, пренебрежимо малой величиной. Полученный результат также означает, что распространенное мнение, будто бы для достижения Луны достаточно достигнуть удаления, на котором притяжения Луны и Земли равны, — неверно. Это подтвердили и расчеты с соответствующих траекторий с учетом притяжения Луны, одна из которых показана на рис. 78. В этом случае за счет влияния притяжения Луны происходит некоторое растяжение начального эллипса и космический аппарат, не достигнув Луны, возвращается к Земле. Любопытно также отметить, что вплоть до момента входа в сферу действия Луны (она на рис. 78 обозначена в виде окружности) фактическая траектория полета очень хорошо совпадает с эллипсом.

Понятно, что величина скорости отлета от Земли целиком определяет продолжительность полета к Луне. Чем больше скорость, тем меньше полетное время. При минимальном значении начальной скорости продолжительность полета составляет немного более четырех суток, при старте с параболической скоростью — около двух суток, а при превышении параболической на 500 м/сек — примерно одни сутки.

Один из наиболее ответственных этапов полета к Луне — это сближение космического аппарата с Луной. Поэтому время полета к Луне выбирают так, чтобы момент сближения был хорошо виден с наземных пунктов управления и наблюдения за полетом. При прямом старте к Луне с территории Советского Союза или старте с первого витка орбиты спутника Земли это требование будет выполнено только в том случае, если продолжительность полета кратна полусуткам, т. е. равна полусуткам, полутора суткам, двум с половиной суткам и т. д. Не случайно поэтому время полета автоматической станции «Луна-2» составляло примерно полутора суток, а в последующих пусках к Луне оно составляло либо 3,5 суток, либо 4,5 суток.

Источник

Задача 24. На Луну со скоростью «Москвича»

Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов

Можно ли достичь Луны в ракете, удаляющейся от Земли со скоростью автомашины?

Из каждых десяти опрошенных двое-трое считают это невозможным. Для полета на Луну нужна вторая космическая скорость – и баста!

Космический век уже создал свои, космические, предрассудки. Надо от них освобождаться. Предыдущая задача показала, что законы небесной механики и законы космонавтики – не одно и то же. Попробуйте преодолеть гипноз космических скоростей: опишите полет к Луне с постоянной умеренной скоростью и ваши впечатления о нем. Вам поможет аналогия: чтобы перебросить камень через 10-метровое дерево, надо придать камню вертикальную скорость порядка 15 м/с; в то же время комар достигает его вершины, двигаясь со скоростью 0,1 м/с.

Вы уже знаете, что совершить круговой полет вокруг Земли можно в принципе с любой скоростью – и больше, и меньше первой космической. Но при этом понадобится держать двигатели все время включенными. Первая космическая скорость нужна для кругового полета с выключенными двигателями.

Это же верно и для полета к Луне. С выключенными двигателями можно достичь Луны только при условии, что у Земли корабль приобрел вторую космическую скорость*. А полет с постоянно включенными двигателями позволяет добраться до Луны при любой скорости.

* Точнее, несколько меньшую. Вторая космическая скорость нужна для параболической орбиты, по которой корабль может уйти от Земли бесконечно далеко. Для полета же к Луне достаточно эллиптической орбиты, апогей которой будет в сфере действия Луны, т.е. там, где тяготение Луны больше тяготения Земли. Массы Земли и Луны относятся как 81 : 1; поэтому точка, где силы тяготения Земли и Луны равны, делит прямую Земля – Луна в отношении √[81] : √[1] = 9 : 1.

Теперь о впечатлениях. Ракета летит равномерно и прямолинейно. Следовательно, в ней нет ни перегрузок, ни невесомости. Состояние такое же, как если бы она была неподвижна в той же точке. Существует естественная весомость в соответствии с законом всемирного тяготения. По мере удаления от Земли сила тяготения убывает обратно пропорционально квадрату расстояния. Именно так нужно регулировать и силу тяги двигателей: сумма сил тяготения и тяги должна равняться нулю, иначе полет перестанет быть равномерным и прямолинейным.

Когда до Луны останется одна десятая часть пути, сила тяги должна обратиться в нуль, так как в этой точке земная сила тяготения уравновешивается лунной и не нуждается в уравновешивании силой тяги. Ракета движется равномерно по инерции. Наступила невесомость. После этого лунное тяготение начинает преобладать над земным. Чтобы поддержать равномерность движения, разверните двигатель соплом к Луне и тормозите. Сила тяги должна быть равна силе тяготения Луны (за вычетом остатков земного тяготения). По мере сближения с Луной сила тяготения возрастает обратно пропорционально квадрату расстояния до Луны. И если так же растет и сила тяги (торможения) двигателей, то движение остается равномерным, а невесомость в корабле постепенно превращается в лунную весомость – около одной шестой от земной.

Стало традицией упрекать Жюля Верна за то, что при описании полета из пушки на Луну он допустил ошибку. Да, он упустил из виду, что в его снаряде невесомость будет на протяжении всего полета. Но зато если бы на место его снаряда поставить ракету из нашей задачи, то жюльверновское описание ощущений космонавтов оказалось бы идеально точным (если не считать непрерывной вибрации от двигателей).

Итак, полет к Луне можно осуществить с комфортом: без перегрузок и почти без невесомости. Такие условия может перенести любой нетренированный человек. Почему же современные корабли летают иначе: с сильной перегрузкой на активном участке полета и с полной невесомостью на орбите? Только из-за необходимости экономить топливо. Для непрерывной работы двигателя при равномерном движении к Луне топлива не хватит. В этом смысле вариант хуже, чем движение с малой постоянной скоростью, придумать нельзя. Впрочем, можно: пусть ракета зависнет неподвижно над Землей. Для поддержания ее в неподвижности потребуется непрерывная работа двигателя. При этом топливо может расходоваться сколь угодно долго, а продвижения вперед не будет.

Этот крайний абсурдный случай показывает, чтО надо делать. Нужно как можно быстрее придать ракете необходимую скорость, чтобы топливо сгорело как можно раньше и не было бы лишних затрат энергии на его подъем на высоту. Циолковский показал, что идеальным является мгновенное сгорание топлива и мгновенный разгон ракеты до нужной скорости. Лучше всего приближается к идеалу пушечный выстрел. «Из пушки на Луну» – довольно экономичный способ космического полета. Но это другая крайность, невозможная из-за недопустимо больших перегрузок космонавтов. Сейчас в космонавтике применяется компромиссный вариант, одинаково далекий от обеих крайностей: на активном участке полета космонавт подвергается большим перегрузкам, но в пределах допустимых, а затем наступает невесомость.

Впрочем, в полете к Луне с постоянной автомобильной скоростью имеется и одно существенное неудобство: при скорости 100 км/ч путешествие к Луне будет длиться 3800 часов, т.е. около 160 суток. И хотя движение к Луне с постоянной скоростью довольно комфортабельно, но эту скорость надо выбирать намного выше.

Прежде чем расстаться с задачей, надо сделать одну оговорку: мы не учитывали, что цель нашего путешествия – Луна – сама движется, причем довольно быстро – со скоростью порядка 1 км/с. Это больше скорости «Москвича», но это не значит, что на Луну нельзя попасть со скоростью автомашины. Орбитальная скорость Луны направлена под прямым углом к трассе нашего «авто» (с небольшими периодическими отступлениями от прямого угла в обе стороны из-за эллиптичности орбиты). И если ракета будет хорошо нацелена в точку встречи с Луной и будет строго выдерживать заданные скорость и направление, то она рано или поздно достигнет Луны при любой скорости удаления от Земли.

При обычном (обычном!) космическом полете (например, вроде того, с помощью которого на Луну доставлен наш вымпел) учет движения Луны необходим. И вы не должны из сноски №16 делать вывод, что для достижения Луны достаточно прибыть в нейтральную точку между Землей и Луной без запаса скорости в надежде, что дальше Луна сама привлечет вас к себе. Ракета, неподвижная относительно Земли, двигалась бы там относительно Луны со скоростью около 1 км/с, а эта скорость на таком расстоянии от Луны является гиперболической (относительно Луны). Иными словами, Луна так быстро убежала бы от ракеты, что та не успела бы разогнаться к Луне ее полем тяготения и, совершив петлеобразное движение, вынуждена была бы вернуться восвояси к Земле. Для достижения Луны ракета должна зайти за нейтральную точку со скоростью 1 км/с, направленной попутно с Луной (и нейтральной точкой). Тогда ракета окажется в неподвижности относительно Луны и, находясь все время в ее поле тяготения, будет ею притянута.

Источник

Скорость для достижения луны

Почти любое сближение автоматической лунной станции (АЛС) или пилотируемого корабля с Луной, будь то облет Луны, падение или посадка на нее или даже простой пролет на более или менее близком расстоянии от Луны, может принести полезную научную информацию. Для определенности мы будем называть сближением с Луной достижение космическим аппаратом любой точки пространства, находящейся внутри сферы действия Луны. Траекториями сближения [3.11 будем называть такие траектории, которые приводят космический аппарат в сферу действия Луны еще до того, как он завершит свой первый оборот вокруг Земли. Последняя оговорка объясняется тем, что сфера действия Луны может быть в принципе достигнута после того, как лунно-солнечные гравитационные возмущения, «расшатав» длинную эллиптическую орбиту спутника Земли, приведут его в конце концов в окрестность Луны (такой случай встретится нам в § 1 гл. 10).

Из всех траекторий сближения наибольший интерес с точки зрения практического использования представляют траектории достижения Луны, или траектории попадания в Луну. Мы сознательно отказываемся от того, чтобы рассматривать полет на Луну как решение задачи о встрече со спутником в том смысле, как это делалось в § 6 гл. 5. В самом деле, нам нет смысла заниматься уравниванием векторов скоростей космического аппарата и Луны, так как это все равно не обеспечило бы безопасного «причаливания» к Луне из-за наличия у нее собственного поля тяготения. Иными словами, мы до поры до времени будем интересоваться попаданием в Луну в «артиллерийском» понимании этого термина. Проблема совершения безопасной посадки на Луну будет рассмотрена позже в этой же главе.

Для выявления основных закономерностей полетов к Луне упростим задачу: будем считать Луну непритягивающей точкой, совпадающей с центром Луны и движущейся по круговой орбите радиуса 384 400 км, или 60,34 радиуса Земли (среднее расстояние Луны от Земли). Позднее мы уточним наши выводы, учитывая и

эллиптичность орбиты Луны, и размер и притяжение естественного спутника Земли, и влияние солнечного притяжения.

Для достижения Луны могут быть использованы кеплеровы траектории любого вида: прямые линии, эллипсы, параболы, гиперболы, но, как увидим далее, местоположение стартовой площадки на земной поверхности и положение Луны в той или иной точке ее орбиты в течение периода обращения (равного 27,3 сут) сильно ограничивают выбор траекторий. Для попадания в Луну необходимо, чтобы траектория пересекла орбиту Луны или по крайней мере коснулась ее.

Если траектория полета эллиптическая, то пересечение орбиты Луны возможно как на восходящей части траектории — до достижения апогея, так и на нисходящей части — после прохождения апогея, расположенного выше орбиты Луны. Эллиптические траектории второго типа, подобные траектории баскетбольного мяча, требуют, очевидно, большего времени перелета и большей точности наведения.

Рис. 68. Трактории достижения Луны при минимальной начальной скорости.

Намечаемое место встречи с Луной выбирается в качестве точки прицеливания впереди Луны с таким расчетом, чтобьг Луна за время перелета пришла в эту «упрежденную» точку орбиты (Луна проходит за сутки дугу 13,2°).

Рассмотрим прежде всего траектории, расположенные в плоскости орбиты Луны; для краткости будем называть их «плоскими». Исследование таких траекторий связано со значительно меньшими трудностями, чем исследование «пространственных» траекторий достижения Луны, не расположенных в плоскости лунной орбиты.

Предположим, что мы стремимся достичь орбиты Луны, сообщая космическому аппарату в некоторой точке А вблизи Земли начальные скорости различного направления.

При вертикальной начальной скорости Луна достигается по прямолинейной траектории 1 (рис. 68), если величина начально? скорости составляет не меньше 11,09 км/с, когда точка А лежит на земной поверхности (теоретический случай), и не меньше

10,9 км/с, если точка А находится на высоте 200 км [3.1] (практически реальный случай). При указанной минимальной вертикальной скорости космический аппарат в точке В достижения орбиты Луны имеет скорость, равную нулю.

Если задаться определенным наклоном начальной скорости к горизонту, то, изменяя величину скорости, мы можем получить различные траектории (рис. 68). Одна из них, а именно эллипс 2 с апогеем, лежащим на орбите Луны, не пересечет эту орбиту, а лишь коснется ее в точке С. Она, очевидно, является траекторией минимальной скорости для заданного направления начальной скорости.

Наконец, в случае горизонтальной начальной скорости мы также будем иметь множество траекторий из которых траекторией минимальной скорости будет полуэллиптическая траектория 3, апогей которой лежит в точке орбиты Луны, диаметрально противоположной точке старта.

Начальная скорость, соответствующая траектории 1, несколько больше скорости отлета, соответствующей траектории 2, а та в свою очередь меньше начальной скорости для траектории 3. Это видно хотя бы из формулы (9) гл. 2, так как входящая в эту формулу большая полуось а у орбиты 3 больше, чем у орбиты 2. Разница в величине а, однако, относительно мала (величина а несколько более где радиус Земли). Как показывает расчет, минимальная начальная горизонтальная скорость больше минимальной вертикальной начальной скорости всего лишь на (для начальной высоты над Землей) [3.1]. Поэтому все траектории, касающиеся орбиты Луны, можно называть траекториями минимальной скорости и считать величину минимальной скорости одинаковой для любого ее направления, а именно равной 11,09 км/с для теоретического случая начала пассивного полета с поверхности Земли и 10,9 км/с для реальной (но, конечно, необязательной) начальной высоты 200 км.

При этом следует иметь в виду, что так как выход на крутую траекторию пассивного полета связан с большими гравитационными потерями на разгон, чем выход на пологие траектории, то из всех траекторий минимальной скорости наиболее выгодна с точки зрения расхода топлива полуэллиптическая.

Обратим внимание на то, что при фиксированном угле возвышения а вектора начальной скорости над горизонтом по мере увеличения начальной скорости траектория все более распрямляется (рис. 68), причем угловая дальность уменьшается. Как известно, при стрельбе по земным целям дело обстоит как раз наоборот. Напомним, что угловая дальность есть угол между

направлениями из центра Земли на начальную и конечную точки полета. Для вертикальной траектории 1 (рис. 68) угловая дальность равна нулю, для траектории 2 — углу для полуэллиптической траектории 3 — углу т. е. 180°. Для параболической траектории с горизонтальной начальной скоростью, как показывает расчет, угловая дальность равна 165° (при высоте начальной точки над поверхностью Земли).

Таким образом, траектории с большой угловой дальностью оказываются более выгодными, так как требуют меньшей начальной скорости.

С другой стороны, если фиксировать величину начальной скорости, но придавать ее вектору различные наклонения (менять угол возвышения вектора скорости над горизонтом), то оказывается, что пологие траектории имеют большую угловую дальность, чем крутые. Например, вертикальная «параболическая» траектория (т. е. прямолинейная траектория при параболической начальной скорости) имеет нулевую угловую дальность, а параболическая траектория с горизонтальной начальной скоростью — угловую дальность 165°. Но запуск на пологую траекторию, как мы знаем, требует меньших затрат топлива.

Таким образом, мы приходим к общему выводу: при полетах к Луне следует стремиться к выбору траекторий с большой угловой дальностью.

Если же угловая дальность фиксирована, т. е. производятся старты из определенной точки земной поверхности (Земля считается невращающейся) в определенную точку орбиты Луны, то существует бесконечное количество траекторий (эллиптических, гиперболических, а также две параболических [3.2]), которые приводят к цели. Главную роль при выборе траектории в этом случае должна играть величина начальной скорости, размер же гравитационных потерь отходит на второй план.

В случае нулевой угловой дальности все возможные траектории представляют собой вертикальные прямые с начальными скоростями, превышающими минимальную.

Случай угловой дальности, равной 180°, является особым: имеется единственная траектория, приводящая к цели, — полуэллиптическая.

При выборе траектории, конечно, важное значение имеет продолжительность перелета. Расчеты показывают, что время перелета до Луны зависит практически лишь от величины начальной скорости, а не от ее направления.

На рис. 69 приведены графики продолжительности полета до Луны по восходящим траекториям при горизонтальной и вертикальной начальных скоростях [3.1]. Как видим, эти графики очень близки между собой. Еще меньше отличаются от указанных графики продолжительности перелетов при промежуточных

наклонах начальных скоростей (типа траектории 2 на рис. 68). На горизонтальной оси рис. 69 отложены значения не самой начальной скорости, а разницы между нею и параболической скоростью на высоте над Землей (где параболическая скорость составляет 11,02 км/с). Мы видим, что время перелета с минимальной скоростью составляет около 5 сут. Увеличение минимальной скорости всего лишь на вдвое сокращает продолжительность перелета. При параболической начальной скорости продолжительность перелета равна уже двум суткам. Сокращение времени перелета до суток возможно при превышении параболической скорости на

Рис. 69. Графики продолжительности полетов до Луны при горизонтальной и вертикальной (2) начальных скоротях [3.1]. Нулевая отметка на оси абсцисс соответствует параболической скорости на высоте

Таким образом, если ставится задача простого попадания в Луну, то незначительное увеличение стартового веса ракеты-носителя или небольшое уменьшение полезной нагрузки уже обеспечивает очень большой выигрыш во времени перелета. Кроме того, как мы увидим, траектории, близкие к параболической, имеют и ряд других преимуществ (см. § 5 настоящей главы).

Заметим, что полет по «плоским» траекториям достижения Луны возможен только в том случае, если место старта находится в плоскости лунной орбиты. Если же место старта находится на некотором удалении, то для осуществления «плоской» траектории понадобится боковой маневр, требующий дополнительного расхода топлива.

Если бы плоскость орбиты Луны совпадала с плоскостью земного экватора, то с любой точки экватора был бы возможен полет к Луне по «плоской» траектории. Правда, не всякая траектория была бы осуществима в любой момент времени. Например, если бы Луна находилась где-то в верхней части орбиты, изображенной

на рис. 68, то заведомо было бы невозможно достичь ее из точки А по выгодной полуэллиптической орбите 3, хотя это и можно было бы сделать с помощью какой-либо из крутых орбит. Однако в течение суток из-за перемещения стартовой площадки вследствие вращения Земли всегда можно было бы выбрать траекторию с любой угловой дальностью.

Фактически, однако, плоскость лунной орбиты наклонена к экваториальной плоскости Земли на угол, который медленно (за 9,3 года) увеличивается от 18°18′ (так уже было, например, в конце декабря 1959 г. и в начале августа 1978 г.) до 28°36′ (конец марта 1969 г., начало ноября 1987 г.) и затем снова уменьшается х). Поэтому полет в плоскости орбиты Луны возможен лишь в том случае, если космодром расположен в прилегающей к экватору зоне, занимающей в наиболее благоприятную эпоху диапазон широт между 28°36′ с. ш. (параллель Дели, Лхасы, мыса Канаверал) и 28°36′ ю. ш., а в самую неблагоприятную эпоху — между 18°18′ с. ш. (параллель Бомбея, Мехико) и 18°18′ ю. ш. Но, даже если космодром находится в указанной зоне, старт возможен лишь в тот момент, когда космодром пересекает (из-за вращения Земли) плоскость орбиты Луны, а это случается лишь дважды в сутки. При этом вполне может оказаться, что Луна находится в такой точке орбиты, что возможен полет лишь по траектории малой угловой дальности, а это, как мы знаем, требует крутого разгона ракеты-носителя. Или может оказаться, что хотя пологий разгон и возможен, но он должен происходить в сторону, противоположную вращению Земли.

Мы, однако, не будем подробнее изучать возможности полетов по «плоским» траекториям, так как даже самый южный пункт Советского Союза расположен в самую благоприятную эпоху на 6° севернее указанной выше экваториальной зоны.

Источник