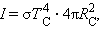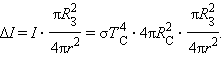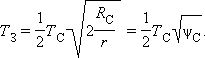Задачи с решениями
Задачи с решениями 

Принимая, что Солнце излучает как абсолютно черное тело с температурой поверхности , оцените среднюю температуру земной поверхности в предположении, что Земля также является абсолютно черным телом, а роль тепловых процессов внутри Земли пренебрежимо мала. Угловой диаметр Солнца, видимый с Земли, примите равным .
В пренебрежении процессами, идущими в недрах Земли, тепловой баланс Земли определяется поглощением энергии солнечного излучения и собственным излучением в пространство. Полный поток энергии , излучаемой Солнцем по всем направлениям, в соответствии с законом Стефана–Больцмана равен
где – постоянная Стефана–Больцмана, – радиус Солнца. Часть полного потока падает на поверхность Земли и поглощается:
Здесь – радиус Земли, – расстояние от Земли до Солнца.
Такой же поток энергии Земля должна излучать в пространство, иначе ее температура не будет оставаться постоянной. Приравнивая поток излучаемой Землей энергии 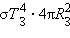
Из этого выражения видно, что для определения нужно знать только температуру поверхности Солнца и его угловой диаметр 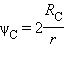
Источник
Считая что солнце излучает как черное тело при температуре найти массу
2018-09-08 
Принимая, что Солнце излучает как черное тело, вычислить его энергетическую светимость $M_
Солнечная постоянная $C$, по определению, есть величина, равная:
где $W$ — энергия, излучаемая Солнцем за время $t$; $S = 4 \pi r^<2>$ — площадь сферической поверхности, радиуса $r$ который равен среднему расстоянию Земли от Солнца.
Энергию, излучаемую Солнцем за время $t$ выразим следующим образом
где $R_
Подставляя выражение (2) в формулу (1) получаем
Выразим площадь поверхности Солнца $S_<0>$ через диаметр $d$ по формуле: $S_ <0>= \pi d^<2>$. Тогда,
Обратимся к рисунку. Так как угол $\theta$ мал, то можно записать, что $d = r \theta$, где угол $\theta$ выражаем в радианах. С учетом этого формула (3) принимает вид:
Отсюда определяем излучательность Солнца
Температуру поверхности Солнца определим воспользовавшись законом Стефана- Больцмана, полагая, что Солнце излучает как абсолютно черное тело.
Согласно закону Стефана — Больцмана излучательность абсолютно черного тела
где $\sigma$ — постоянная Стефана — Больцмана ($\sigma = 5,67 \cdot 10^ <-8>\frac<Вт> <м^<2>\cdot К^ <4>>$ ). Отсюда
Подставляя в это выражение значение $\sigma$ и найденное выше значение $R_
Источник
Считая что солнце излучает как черное тело при температуре найти массу
Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:
1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.
2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.
3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2
4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.
5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.
6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь
8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.
9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.
10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.
11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0
12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.
13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.
14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.
Источник
Считая что солнце излучает как черное тело при температуре найти массу
1. Эталон единицы силы света — кандела — представляет собой полный (излучающий волны всех длин) излучатель, поверхность которого площадью S=0,5305 мм2 имеет температуру t затвердевания платины, равную 1063 °С. Определить мощность Р излучателя.
→ Перейти к решению
2. Определить температуру Т абсолютно чёрного тела, если оно излучает с S = 1 см2 в минуту W = 2226 Дж.
→ Перейти к решению
3. Во сколько k раз возрастёт энергетическая светимость поверхности абсолютно чёрного тела, если повысить температуру тела от Т = 2100 К (температура нити угольной лампы накаливания) до 1) Т1 = 2400 К (температура вольфрамовой нити вакуумной лампы) и до 2) Т2 = 2735 К (температура нити в газонаполненной лампе)?
→ Перейти к решению
4. На сколько надо повысить температуру абсолютно чёрного тела (полного излучате- ля) для того, чтобы интегральная энергетическая светимость его поверхности увели- чилась в k = 200 раз? Температура полного излучателя t = 527 ○C.
→ Перейти к решению
5. Определить мощность Р, необходимую для поддержания температуры расплавленной платины Т = 2050 К неизменной, если площадь поверхности платины S= 1 см2. Расплавленную платину можно считать абсолютно чёрным телом и поглощением лучистой энергии от окружающих тел можно пренебречь.
→ Перейти к решению
6. До какой температуры Т необходимо было бы нагреть абсолютно чёрное тело для того, чтобы плотность потока энергии вблизи его поверхности совпадала бы с плот-ностью энергии в лазерном луче диаметром d = 1 мм? Мощность излучения лазера Р=10 мВт.
→ Перейти к решению
7. Внутри полости, ограниченной зеркальной оболочкой, находится нагретое до тем- пературыТ небольшое абсолютно чёрное тело. Определить объёмную плотность uэнергии равновесного теплового излучения, существующего в полости.
→ Перейти к решению
8. Полость, ограниченная зеркальной оболочкой, заполнена равновесным тепловым излучением, созданным абсолютно чёрным телом объёма, небольшого по сравнению с объёмом полости. Тело нагрето доТ = 500 К. Определить удельную теплоёмкость сVпространства полости, заполненного излучением.
→ Перейти к решению
9. В закрытом сосуде находится идеальный одноатомный газ с концентрацией молекул n= 1,9·1025м–3. При какой температуреТ объёмная плотность кинетической энергии молекул будет равна объёмной плотности энергии uравновесного теплового излуче- ния при этой же температуре?
→ Перейти к решению
10. Внутри полости, ограниченной зеркальной оболочкой, находится небольшое абсо- лютно чёрное тело. Полагая, что теплоёмкость тела не зависит от температуры, оце- нить, какую часть от внутренней энергии Uтела составляет энергия Wтеплового из- лучения в полости. Для оценок принять температуру телаТ = 300 К, теплоёмкость тела С = 3000 Дж/К, объём полости V = 2 м3.
→ Перейти к решению
11. Определить поглощательную способность серого тела, если оно при температуре t = 727○C с поверхности S = 10 см2 испускает лучистый поток 25 Вт. Лучистым потоком, падающим на тело от окружающих предметов, можно пренебречь. Указание: Серым телом называется такое тело, поглощательная способность которого не зависит от длины волны.
→ Перейти к решению
12. Найти площадь S излучающей поверхности нити 25-ваттной лампы, если температура нити Т = 2450 К. Излучение нити составляет р = 30% излучения абсолютно чёрного тела при данной температуре. Потерями тепла, связанными с теплопроводностью, пренебречь.
→ Перейти к решению
13. При какой температуре t1интегральная энергетическая светимость поверхности серого тела с коэффициентом излучения 0,656 равна энергетической светимости абсолютно чёрного тела, имеющего температуру t = 2127○C?
→ Перейти к решению
14. Мощность Р излучения шара радиусом R = 10 см при некоторой постоянной темпе- ратуреТ равна 1 кВт. Найти эту температуру, считая шар серым телом с коэффици- ентом теплового излучения = 0,25.
→ Перейти к решению
15. Можно условно считать, что Земля излучает как серое тело, находящееся при температуре Т = 280 К. Определить коэффициент теплового излучения Земли, если энергетическая светимость Re её поверхности равна 325 кДж/(м2 ч).
→ Перейти к решению
16. Принимая коэффициент теплового излучения угля при температуреТ = 600 К рав- ным 0,8, определить 1) энергетическую светимость Reугля; 2) энергию W, излучае- мую с поверхности угля с площадью S= 5 см2 за время t =10 мин.
→ Перейти к решению
17. Вычислить лучистый поток , испускаемый кратером дуги с простыми углями, имеющим температуруТ = 4200 К. Диаметр кратера d = 7 мм. Излучение угольной дуги составляет приблизительно р = 80% излучения абсолютно чёрного тела при данной температуре.
→ Перейти к решению
18. Температура поверхности Солнца ТС= 6000 К. Полагая, что поглощательная способ- ность Солнца и Земли равна единице и что Земля находится в состоянии теплового равновесия, оценить её температуру ТЗ. Расстояние от Земли до Солнцаr = 1,5108 км, радиус Солнца RC = 6,5105 км.
→ Перейти к решению
19. Вычислить температуруТ поверхности Солнца, принимая что Солнце излучает как абсолютно чёрное тело. На S = 1 см2 земной поверхностипадает лучистый поток = 8,1 Дж/мин (с учётом энергии, поглощаемой земной атмосферой). Расстояние от Земли до Солнцаr = 1,5108км, радиус Солнца RC = 6,5105км.
→ Перейти к решению
20. Медный шарик диаметра d = 1,2 см поместили в откачанный сосуд, температура которого поддерживается близкой к абсолютному нулю. Начальная температура шарика Т0 = 300 К. Считая поверхность шарика абсолютно чёрной, найти, через сколько времени его температура уменьшится в 2 раза. Удельная теплоёмкость меди с = 390 Дж/(кг К), плотность меди 8,9×10^3 кг/м3.
→ Перейти к решению
21. Теплопроводящий шар по размеру равен Земле (R = 6400 км). Удельная теплоём- кость с = 200 Дж/кг·К, плотность= 5500 кг/м3. Начальная температура Т0 = 300 К.
Определить времяr, за которое шар остынет на ∆Т = 0,001 К. Шар считать абсолют-
но чёрным.
→ Перейти к решению
22. Тело с массой m = 10 г и поверхностью S= 200 см2, имеющее температуру Т1 = 600 К, помещено в вакуум. Определить до какой температуры Т2 охладится тело за 30 с, если поглощательная способность поверхности тела равна 0,4, а удельная теплоёмкость с составляет 330 Дж/(кг К). Лучистым потоком, падающим на тело вследствие излучения окружающих предметов, пренебречь.
→ Перейти к решению
23. Определить за какое время медный шар, помещённый в вакуум, охладится с Т1 = 500 К до Т2 = 300 К. Радиус шара r = 1 см, поглощательная способность поверх- ности шара = 0,8, удельная теплоёмкость меди с = 390 Дж/(кгК), плотность меди
= 8,93 кг/м3. Излучением, падающим на поверхность шара от окружающих предметов, пренебречь.
→ Перейти к решению
24. Считая, что тепловые потери обусловлены только излучением, определить, какую мощность Р необходимо подводить к медному шарику диаметром d = 2 см, чтобы при температуре окружающей среды t0 = 13 ○C поддерживать его температуру равной t = 17 ○C. Принять поглощательную способность меди 0,6.
→ Перейти к решению
25. Определить силу тока I, протекающего по вольфрамовой проволокедиаметром d
= 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t
= 2800 ○C. Поверхность проволоки принять в качестве серой с поглощательной спо- собностью = 0,343. Удельное сопротивление проволоки при данной температуре
= 0,9210Омсм. Температура окружающей проволоку среды t = 17 ○C.
→ Перейти к решению
26. Отношение интегральной энергетической светимости некоторого тела к интегральной энергетической светимости абсолютно чёрного тела при той же температуре равно 0,36. Определить, во сколько k раз отличается истинная температура от радиационной.
→ Перейти к решению
27. Определить истинную температуруТ вольфрама, если его радиационная температура ТR = 2030 К и отношение интегральной энергетической светимости вольфрама к ин- тегральной энергетической светимости абсолютно чёрного тела при указанной тем- пературе равно 0,318 (см. задачу 26).
→ Перейти к решению
28. На какую длину волны приходится максимум излучения абсолютно чёрного тела, если температура тела t = 0 ○C? В какой области спектра лежит максимум излуче- ния?
→ Перейти к решению
29. На какую длину волны приходится максимум энергии излучения абсолютно чёр- ного тела при температуре: 1) t1 = 100 ○C; 2)t2 = 5000 ○C; 3) t3 = 10000 ○C?
→ Перейти к решению
30. Максимум излучения полного излучателя (абсолютно чёрного тела) приходится на длину волны 0,58 мкм. Определить лучистый поток, испускаемый излучателем, если площадь его поверхности S= 4 см2.
→ Перейти к решению
31. Максимум излучения абсолютно чёрного тела приходится на длину волны = 250 нм. На какую длину волны 1 придётся максимум излучения, если темпера- туру тела повысить на t = 50 ○C?
→ Перейти к решению
32. Вследствие изменения температуры абсолютно чёрного тела максимум спектральной плотности (r T) max сместился с 2,4 мкм на 0,8 мкм. Как и во сколько раз изменилась энергетическая светимость Re тела и максимальная спектральная плотность энергетической светимости?
→ Перейти к решению
33. Чёрное тело находится при температуре Т1 = 3 кК. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на 8 мкм. Определить температуру Т2, до которой тело охладилось.
→ Перейти к решению
34. При увеличении термодинамической температуры чёрного тела в два раза длина волны m, на которую приходится максимум спектральной плотности энергетиче- ской светимости (rT)max, уменьшилась на = 400 нм. Определить начальную Т1 и конечную Т2 температуры.
→ Перейти к решению
35. Энергетическая светимость чёрного тела Re = 3,0 Вт/см2. Определить длину волны
m, отвечающую максимуму спектральной испускательной способности этого тела.
→ Перейти к решению
36. Принимая Солнце за чёрное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны m = 0,5 мкм, оп- ределить: 1) температуруТ поверхности Солнца; 2) энергию W, излучаемую Солн- цем за t = 10 мин; 3) массу m, теряемую Солнцем за это время за счёт излучения.
→ Перейти к решению
37. Температура чёрного телаТ = 2 кК. Определить: 1) спектральную плотность энерге- тической светимости (rT) для длины волны = 600 нм; 2) энергетическую свети- мость Reв интервале длин волн от 1 = 590 нм до 2 = 610 нм. Принять, что средняя спектральная плотность энергетической светимости тела в этом интервале равна значению, найденному для длины волны = 600 нм.
→ Перейти к решению
38. Вычислить, во сколько раз увеличится энергетическая светимость абсолютно чёрно- го тела в небольшом интервале длин волн возле длины волны = 5 мкм при повы- шении температуры от Т1= 1000 К до Т2= 2000 К.
→ Перейти к решению
39. Температура абсолютно чёрного телаТ = 500 К. Вычислить энергетическую свети- мость Re, приходящуюся на спектральный интервал длин волн = 0,1 мкм, возле длины волны = 0,58 мкм. Найти энергетическую светимость Re, в таком же интер- вале длин волн возле длины волны, соответствующей максимуму спектральной плотности энергетической светимости тела.
→ Перейти к решению
40. Вычислить спектральную плотность rT энергетической светимости абсолютно чёр- ного тела при температуреТ = 2400 К для длины волны 1 = 0,5 мкм и длины волны
2 = 5 мкм. Которое из этих двух вычислений можно сделать по формуле Вина, а ко- торое только по формуле Планка?
→ Перейти к решению
41. Излучение абсолютно чёрного тела, имеющего температуру Т = 2400 К, падает на светофильтр, который пропускает 90% излучения в области длин волн от 0,5 мкм до 0,4 мкм и совершенно не пропускает излучения с длинами волн вне указанной области. Вычислить, какую долю полного падающего потока пропускает светофильтр.
→ Перейти к решению
42. Вычислить спектральную энергетическую светимость тела rT для длины волны
= 0,5 мкм при температуреТ = 2100 К, если спектральная поглощательная способ- ность Т при тех же температуре и длине волны равна 0,8.
→ Перейти к решению
43. Температура чёрного телаТ = 3000 К. Определить максимальную спектральную энергетическую светимость (rT)max.
→ Перейти к решению
44. Для длины волны = 0,6 мкм спектральная энергетическая светимость равна спек- тральной энергетической светимости абсолютно чёрного тела, имеющего темпера- туру Т0= 3000 К. Вычислить температуру Т тела, если его спектральная поглоща- тельная способность Тдля данной длины волны равна 0,5.
→ Перейти к решению
45. Оптическим пирометром, снабжённым фильтром, пропускающим излучение с дли- ной волны = 0,665 мкм, измерена яркостная температура тела. Определить истин- ную температуру Т1тела, если яркостная температура Т2 = 2600 К. Коэффициент из- лучения поверхности тела = 0,8.
Указание. Яркостной температурой тела называется такая температура, при которой абсо- лютно чёрное тело имеет при определённой длине волны ту же монохроматическую яр- кость излучения, что и данное тело. Связь между истинной температурой Т1 и яркостной температурой Т2 для серого тела с коэффициентом излучения выражается формулой Т1 = С2/(ln+ C2/T2), где С2постоянная в формуле распределения Планка, равная 1,4410мК.
→ Перейти к решению
46. Температура вольфрамовой пластинки Т1 = 2500 К. Вычислить яркостную темпера- туру Т2, которая будет определена для такой пластинки с помощью оптического пи- рометра с применением фильтра, пропускающим излучение с длиной волны = 0,467 мкм. Коэффициентизлучениявольфрама= 0,462.
→ Перейти к решению
47. Истинная температура вольфрамовой пластинки Т1 = 2400 К. Яркостная температура той же пластинки, измеренная оптическим пирометром с применением фильтра, пропускающего излучение с длиной волны = 0,665 мкм, Т2 = 2190 К. Вычислить коэффициент излучения поверхности пластинки для данной длины волны и темпе- ратуры.
→ Перейти к решению
48. Найти число фотонов n, испускаемых с 1 см2 в 1 с с поверхности абсолютно чёрного тела, имеющего температуру Т= 6000 К, в интервале длин волн от 0,5 мкм до 0,55 мкм.
→ Перейти к решению
49. Температура абсолютно чёрного тела Т = 4000 К. Определить число фотонов n, испускаемых с 1 см2 в 1 с с поверхности тела в области длин волн, соответствующих максимальной спектральной энергетической светимости, в спектральном интервале 0,1 мкм.
→ Перейти к решению
50. Нить лампы накаливания излучает как абсолютно чёрное тело, имеющее температу- руТ = 2400 К. Вычислить, сколько фотонов nиспускается с 1 см2 поверхности нити в 1 с, если среднюю энергию кванта излучения можно считать равной 2,75 kT.
→ Перейти к решению
51. Точечный изотропный источник испускает свет с 589 нм. Световая мощность источника Р = 10 Вт. Найти: 1) среднюю плотность потока фотонов на расстоянии r = 2 м от источника; 2) расстояние r1 от источника до точки, где средняя концентрация фотонов n = 100 см-3.
→ Перейти к решению
52. Определить эффективную температуру Тэ лазерного луча, если лазер, работая в им- пульсном режиме, излучаетЕ = 1 МВт/см2 в интервале частот = 109 Гц. Длина волны лазера = 1 мкм. Эффективной температурой лазерного луча называется температура, до которой надо было бы нагреть абсолютно чёрное тело, чтобы оно излучало в той же спектральной области, что и лазер, одинаковую с ним энергию.
→ Перейти к решению
53. Мощность рубинового лазера, работающего в импульсном режиме, Р = 10 кВт в им- пульсе с площади S = 1 см2. Определить эффективную температуру Тэ лазерного лу- ча, если длина волны излучения рубинового лазера = 694,3 нм, ширина полосы
= 0,002 нм.
→ Перейти к решению
54. Найти температуруТ полностью ионизованной водородной плазмы плотностью ρ = 0,10 г/см3, при которой давление теплового излучения равно газокинетическому давлению частиц плазмы. Иметь в виду, что давление теплового излучения р = u/3, где u―объёмная плотность энергии излучения, и что при высоких температурах ве- щества подчиняются уравнению состояния идеальных газов. Молярная масса водо- рода µ = 2 г/моль.
→ Перейти к решению
55. На S = 1 см2 поверхности падает лучистый поток мощностью Р = 1 мкВт. Опреде- лить давление р света, если коэффициент отражения ρ = 0,8. Поверхность перпенди- кулярна лучам.
→ Перейти к решению
56. Вычислить световое давление на идеальную зеркальную поверхность, площадь которой составляет S = 10 см2, если на неё падает лучистый поток Р = 0,9 Вт. Поверхность перпендикулярна лучам.
→ Перейти к решению
57. Энергетическая освещённость Е поверхности с коэффициентом отражения ρ = 0,62 равна 0,8 Вт/см2. Определить: 1) величину светового давления р на поверхность; 2) сколько процентов x1 от полного давления составляет давление, связанное с отражёнными фотонами; 3) сколько процентов x2 полного давления составляет давление, связанное с поглощёнными фотонами.
→ Перейти к решению
58. Определить силу F светового давления солнечного излучения на поверхность земного шара, считая её абсолютно чёрной и не учитывая поглощения излучения в атмосфере Земли. Если бы атмосфера не поглощала, то S = 1 см2 земной поверхности, расположенный перпендикулярно лучам, получал бы около Р = 0,15 Дж/c. Радиус Земли R = 6400 км.
→ Перейти к решению
59. Колба электрической лампы представляет собой сферу радиусом R = 3.3 см. Часть стенки колбы изнутри посеребрена. Лампа потребляет мощность Р = 40 Вт, из которых x = 85% затрачивается на излучение. Определить, во сколько раз давление газа в колбе р = 1,3×10−5 Па меньше светового давления на посеребрённую часть колбы.
→ Перейти к решению
60. В опытах П.Н.Лебедева, доказавшего существование светового давления, энергетическая освещённость соответствовала примерно Е = 1045 Вт/м2. Вычислить давление р, которое должны были испытывать а) зачернённые и б) зеркальные лепестки измерительной установки.
→ Перейти к решению
61. Лазер излучил в импульсе длительностью τ = 0,13 мс пучок света с энергией W = 10 Дж. Найти среднее давление р такого светового импульса, если его сфокусировать в пятнышко диаметром d = 10 мкм на поверхность, перпендикулярную к пучку, с ко- эффициентом отражения ρ = 0,5.
→ Перейти к решению
62. Определить энергию W твёрдотельного лазера в импульсе длительностью τ = 100 нс, если лазерный луч площадью поперечного сечения S = 1 см2, падающий на расположенную нормально к нему зеркальную пластинку, оказывает давление р = 6,6×107 Па.
→ Перейти к решению
63. Длина волну излучения рубинного лазера λ = 694,3 нм. Лазер излучает в импульсе длительностью τ = 1 мс энергию W = 10 Дж. 1) Вычислить давление р лазерного луча, сфокусированного линзой на экран, расположенный перпендикулярно лазерному лучу в пятно, площадь которого S1 = λ2. Коэффициент отражения экрана ρ = 0,5. 2) Сравнить результат с давлением несфокусированного лазерного луча, площадь по- перечного сечения которого S1 =1 см2.
→ Перейти к решению
64. Вычислить давление р лазерного луча на зеркальную поверхность пластинки, расположенной перпендикулярно лазерному лучу. Мощность Р лазера в импульсе составляет 1 МВт, площадь поперечного сечения лазерного луча S = 1 см2. Считать, что мощность лазера в импульсе постоянна.
→ Перейти к решению
65. На зеркальную поверхность площадью S = 10см2 падает под углом α = 450 пучок фотонов интенсивностью N=1,0·1018 фотон/c. Длина волны падающего света λ = 400 нм. Определить величину светового давления р на поверхность.
→ Перейти к решению
66. Давление р монохроматического света с длиной волны λ = 500 нм на зачернённую поверхность, расположенную перпендикулярно падающему излучению, равно 0,15 мкПа. Определить число N фотонов, падающих на поверхность площадью S = 40см2 за одну секунду.
→ Перейти к решению
67. Давление р монохроматического света с длиной волны λ = 600 нм на зачернённую поверхность, расположенную перпендикулярно падающему излучению, равно 0,1 мкПа. Определить: 1) концентрациюnфотонов в световом пучке; 2) число N фото- нов, падающих ежесекундно на S = 1м2 поверхности.
→ Перейти к решению
68. На идеально отражающую плоскую поверхность нормально падает монохроматический свет с длиной волны λ = 550 нм. Поток излучения Ф составляет 0,45 Вт. Определить: 1) число N фотонов, падающих на поверхность за время t = 3 c; 2) силу давления F, испытываемую этой поверхностью.
→ Перейти к решению
69. Плоская световая волна интенсивностью I = 0,1 Вт/см2падает под углом α = 300 на плоскую отражающую поверхность с с коэффициентом отражения ρ = 0,7. Исполь- зуя квантовые представления, определить нормальное давление р, оказываемое све- том на эту поверхность.
→ Перейти к решению
70. Оценить порядок величины диаметра d сферической космической частицы, для ко- торой сила притяжения к Солнцу уравновешивается силой светового давления сол- нечного излучения. Поверхность частицы можно считать абсолютно чёрной, а плот- ность частицы равной ρ = 7,8 г/см3. Принять, что Солнце излучает как абсолютно чёрное тело с температурой ТС = 6000 К. Масса Солнца МС = 1,97·1030 кг, радиус Солнца RC = 6,96·105км.
→ Перейти к решению
Источник
 Задачи с решениями
Задачи с решениями