Видимое годовое движение солнца на небесной сфере
Истинное движение Земли — Видимое годовое движение Солнца на небесной сфере — Небесный экватор и плоскость эклиптики — Экваториальные координаты Солнца в течение года
Истинное движение Земли
Чтобы понять принцип видимого движения Солнца и других светил на небесной сфере, рассмотрим сперва истинное движение Земли. Земля является одной из планет солнечной системы. Она непрерывно вращается вокруг своей оси.
Период вращения ее равен одним суткам, поэтому наблюдателю, находящемуся на Земле, кажется, что все небесные светила обращаются вокруг Земли с востока на запад с тем же периодом.
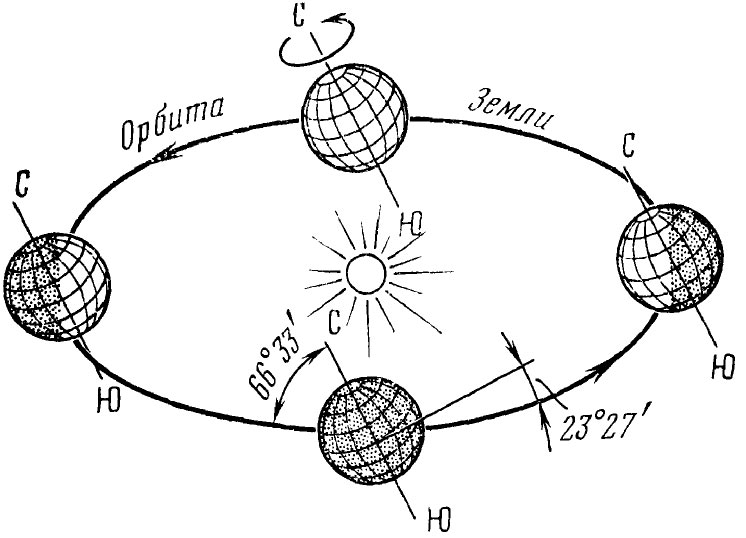
Наклон оси вращения Земли к плоскости орбиты
Но Земля не только вращается вокруг своей оси, но и обращается также вокруг Солнца по эллиптической орбите. Полный оборот вокруг Солнца она совершает за один год. Ось вращения Земли наклонена к плоскости орбиты под углом 66°33′. Положение оси в пространстве при движении Земли вокруг Солнца все время остается почти неизменным. Поэтому Северное и Южное полушария попеременно бывают обращены в сторону Солнца, в результате чего на Земле происходит смена времен года.
При наблюдении неба можно заметить, что звезды на протяжении многих лет неизменно сохраняют свое взаимное расположение.
Звезды “неподвижны” лишь потому, что находятся очень далеко от нас. Расстояние до них так велико, что с любой точки земной орбиты они видны одинаково.
А вот тела же солнечной системы — Солнце, Луна и планеты, которые находятся сравнительно недалеко от Земли, и смену их положений мы можем легко заметить. Таким образом, Солнце наравне со всеми светилами участвует в суточном движении и одновременно имеет собственное видимое движение (оно называется годовым движением), обусловленное движением Земли вокруг Солнца.
Представьте себе картину — Луна взяла и исчезла с орбиты Земли. Чем нам может грозить такой поворот событий? Подробнее об этом
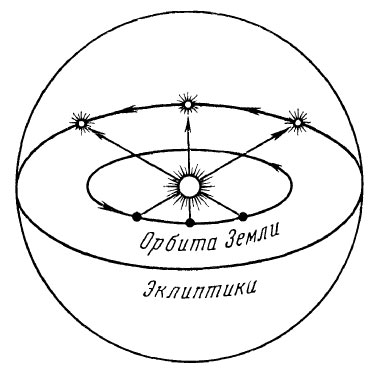
Видимое годовое движение Солнца на небесной сфере
Наиболее просто годовое движение Солнца можно объяснить по рисунку приведенному ниже. Из этого рисунка видно, что в зависимости от положения Земли на орбите наблюдатель с Земли будет видеть Солнце на фоне разных созвездий. Ему будет казаться, что оно все время перемещается по небесной сфере. Это движение является отражением обращения Земли вокруг Солнца. За год Солнце сделает полный оборот.
Что представляет собой эклиптика
Большой круг на небесной сфере, по которому происходит видимое годовое движение Солнца, называется эклиптикой. Эклиптика — слово греческое и в переводе означает затмение. Этот круг назвали так потому, что затмения Солнца и Луны происходят только тогда, когда оба светила находятся на этом круге.
Следует отметить, что плоскость эклиптики совпадает с плоскостью орбиты Земли.
Видимое годовое движение Солнца по эклиптике происходит в том же направлении, в котором Земля движется по орбите вокруг Солнца, т. е. оно перемещается к востоку. В течение года Солнце последовательно проходит по эклиптике 12 созвездий, которые образуют пояс Зодиака и называются зодиакальными.
Пояс Зодиака образуют следующие созвездия: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог и Водолей. Вследствие того, что плоскость земного экватора наклонена к плоскости орбиты Земли на 23°27 ‘ , плоскость небесного экватора также наклонена к плоскости эклиптики на угол е=23°27′.
Наклон эклиптики к экватору не сохраняется постоянным (вследствие воздействия на Землю сил притяжения Солнца и Луны), поэтому в 1896 г. при утверждении астрономических постоянных решено было наклон эклиптики к экватору считать усредненно равным 23°27’8″,26.
Небесный экватор и плоскость эклиптики
Эклиптика пересекается с небесным экватором в двух точках, которые называются точками весеннего и осеннего равноденствий. Точку весеннего равноденствия принято обозначать знаком созвездия Овен Т, а точку осеннего равноденствия — знаком созвездия Весов —. Солнце в этих точках соответственно бывает 21 марта и 23 сентября. В эти дни на Земле день равен ночи, Солнце точно восходит в точке востока и заходит в точке запада.
Точки весеннего и осеннего равноденствия – места пересечения экватора и плоскости эклиптики
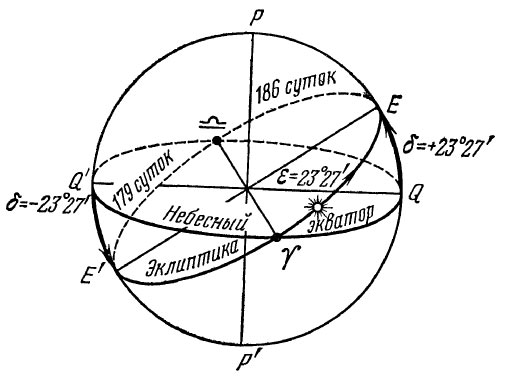
Точки эклиптики, отстоящие от точек равноденствий на 90°, называются точками солнцестояний. Точка Е на эклиптике, в которой Солнце занимает самое высокое положение относительно небесного экватора, называется точкой летнего солнцестояния, а точка Е’, в которой оно занимает самое низкое положение, называется точкой зимнего солнцестояния.
В точке летнего солнцестояния Солнце бывает 22 июня, а в точке зимнего солнцестояния — 22 декабря. В течение нескольких дней, близких к датам солнцестояний, полуденная высота Солнца остается почти неизменной, в связи с чем эти точки и получили такое название. Когда Солнце находится в точке летнего солнцестояния день в Северном полушарии самый длинный, а ночь самая короткая, а когда оно находится в точке зимнего солнцестояния — наоборот.
В день летнего солнцестояния точки восхода и захода Солнца максимально удалены к северу от точек востока и запада на горизонте, а в день зимнего солнцестояния они имеют наибольшее удаление к югу.
Движение Солнца по эклиптике приводит к непрерывному изменению его экваториальных координат, ежедневному изменению полуденной высоты и перемещению по горизонту точек восхода и захода.
Известно, что склонение Солнца отсчитывается от плоскости небесного экватора, а прямое восхождение — от точки весеннего равноденствия. Поэтому когда Солнце находится в точке весеннего равноденствия, его склонение и прямое восхождение равны нулю. В течение года склонение Солнца в настоящий период изменяется от +23°26′ до —23°26′, переходя два раза в год через нуль, а прямое восхождение от 0 до 360°.
Солнце имеет форму шара или сплюснуто у полюсов? Давайте разберемся! Подробнее об этом
Экваториальные координаты Солнца в течение года
Экваториальные координаты Солнца в течение года изменяются неравномерно. Происходит это вследствие неравномерности движения Солнца по эклиптике и движения Солнца по эклиптике и наклона эклиптики к экватору. Половину своего видимого годового пути Солнце проходит за 186 суток с 21 марта по 23 сентября, а вторую половину за 179 суток с 23 сентября по 21 марта.
Неравномерность движения Солнца по эклиптике связана с тем, что Земля на протяжении всего периода обращения вокруг Солнца движется по орбите не с одинаковой скоростью. Солнце находится в одном из фокусов эллиптической орбиты Земли.
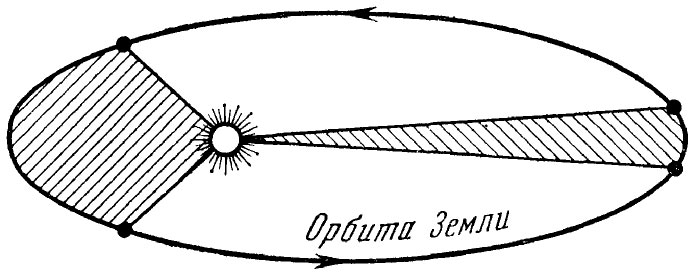
движение Земли по орбите
Из второго закона Кеплера известно, что линия, соединяющая Солнце и планету, за равные промежутки времени описывает равные площади. Согласно этому закону Земля, находясь ближе всего к Солнцу, т. е. в перигелии, движется быстрее, а находясь дальше всего от Солнца, т. е. в афелии — медленнее.
Ближе к Солнцу Земля бывает зимой, а летом — дальше. Поэтому в зимние дни она движется по орбите быстрее, чем в летние. Вследствие этого суточное изменение прямого восхождения Солнца в день зимнего солнцестояния равно 1°07′, тогда как в день летнего солнцестояния оно равно только 1°02′.
Различие скоростей движения Земли в каждой точке орбиты вызывает неравномерность изменения не только прямого восхождения, но и склонения Солнца. Однако за счет наклона эклиптики к экватору его изменение имеет другой характер. Наиболее быстро склонение Солнца изменяется вблизи точек равноденствия, а у точек солнцестояния оно почти не изменяется.
Знание характера изменения экваториальных координат Солнца позволяет производить приближенный расчет прямого восхождения и склонения Солнца.
Для выполнения такого расчета берут ближайшую дату с известными экваториальными координатами Солнца. Затем учитывают, что прямое восхождение Солнца за сутки изменяется в среднем на 1°, а склонение Солнца в течение месяца до и после прохождения точек равноденствия изменяется на 0,4° в сутки; в течение месяца перед солнцестояниями и после них — на 0,1° в сутки, а в течение промежуточных месяцев между указанными — на 0,3°.
Источник
Расчет траектории движения солнца
Submit your questions, suggestions
and criticisms here:
| Help & API |  |
SunCalc shows the movement of the sun and sunlight-phase for a certain day at a certain place.
You can change the suns positions for sunrise , selected time and sunset see. The thin yellow-colored curve shows the trajectory of the sun, the yellow deposit shows the variation of the path of the sun throughout the year. The closer a point in the center, the higher the sun above the horizon. The colors in the above time-slider shows the sunlight during the day. The sun on the time slider can be moved by mouse or with the arrow keys of the keyboard
| API to link to this page! API for developers |  |
| The same for the Moon |  |
| Donate |  |
With a small donation you can go to Contribute to the preservation of this website. The amount is free selectable and is done via PayPal .
Thank you
| Legal Disclosure / Privacy Policy |  |
Information in accordance
with section 5 TMG:
Torsten Hoffmann
Robert-Schumann-Str. 17
67304 Eisenberg
Germany
Источник
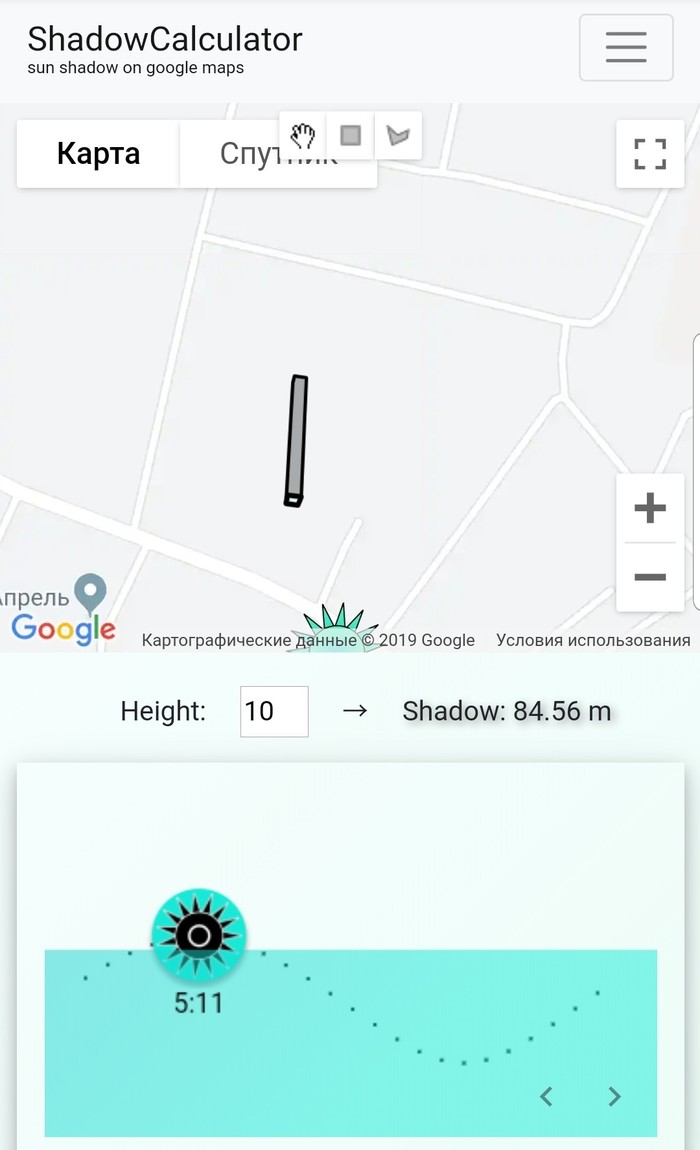
Калькулятор тени / ShadowCalculator
В сети есть сайт shadowcalculator.eu , где можно посмотреть позицию солнца на картах Google.
Тоесть.. Если вы планируете построить дом за городом, и хотите понять как будет падать тень от дома на ваш огород то можно «предсказать» эту тень..
Дубликаты не найдены
ТС прям вообще молодец, а я ещё думал, чем бы мне заняться завтра
Что будем делать завтра, Иван?
Что-то я конкретно туплю. А вот просто на участке посмотреть с какой стороны солнце, с какой тень и сразу понять где они будут утром и вечером — это уже никак?
Ну. Если я провел день на участке и если я был примерно трезв и зряч, то определю. Просто, если помнить, что солнце у нас обычно встает на востоке на уровне горизонта, садится на уровне горизонта на западе, а днем оно обычно с южной стороны, то все становится более-менее предсказуемо. По крайней мере, на практике я еще не ошибался.
Это применимо скорее для выбора участка для покупки, на каждом в округе по дню проводить достаточно хлопотно.
Тут все еще проще. Если я прибыл на участок, и я опять же более-менее трезв и зряч, я вижу как сориентирован участок по сторонам света. И если с южной стороны девятиэтажка, то разумно предположить, что участок большую часть дня будет в тени. А если с северной стороны растут деревья, то это будет наоборот в плюс. Эти выводя можно сделать даже пасмурным днем.
Ну хоть солнце бесплатно.
Аналемма — траектория движения солнца по небосводу, в зависимости от времени года.
Сервис наложения аналеммы на карту Гугл.
https://daybit.ru/sun/
24 петли, это 24 часа соответственно.
А местоположение солнца в петле, соответствует времени года (месяц, дата)
Таким образом можно выбрав дату смотреть под каким углом к горизонту проходит солнце в каждый час суток.
В каком месте восходит, а в каком заходит.
Верхние точки петель — это максимальный подъем солнца летом, и линия движения солнца соответственно.
Нижняя точка петель — подъем солнца зимой.
Источник
Расчет положения небесных тел на небосводе. Часть 1
Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.
В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.
Всех любопытных прошу под кат.
Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.
Так как же движутся планеты?
В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.
Кеплерова орбита
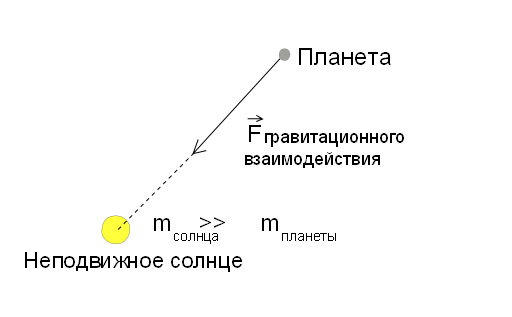
Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так:
Гравитационное взаимодействие
Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: 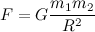
Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу сферическую планету в вакууме материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.
Второй закон Ньютона
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость: 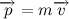
Таким образом, запишем словесную формулировку в символьном виде: 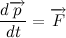
Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу: 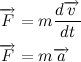
Где вектор 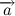
Второй закон Кеплера
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).
Дифференциальное уравнение орбиты
Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором: 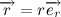

Тогда вектор скорости будет равен: 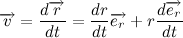
А векторное произведение радиус вектора на скорость в свою очередь: 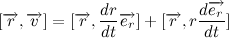
Учитывая тот факт, что вектора 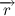
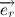
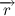



Давайте разберем, что такое производная единичного вектора по времени: 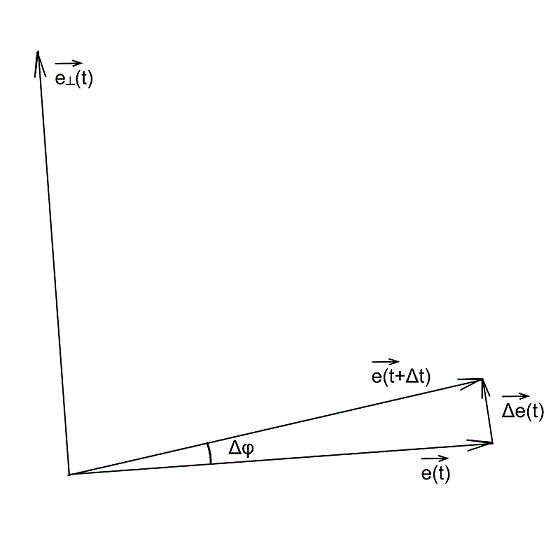
Из рисунка видно, что за время 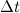
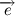
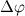
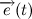

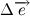

В пределе, когда 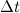
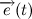

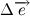
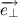
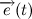
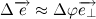
Таким образом, переходя к пределу, получим: 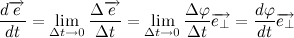
Где 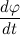
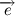
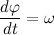
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что 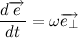
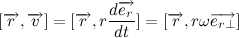
Несложно заметить, что вектора 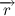
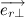
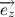
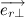
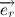
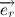
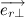
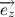
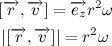
Следовательно, 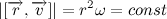
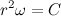

Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт 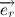
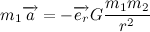
Где m1 и m2 — масса планеты и солнца соответственно.
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, 
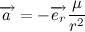
Теперь давайте распишем вектор ускорения: 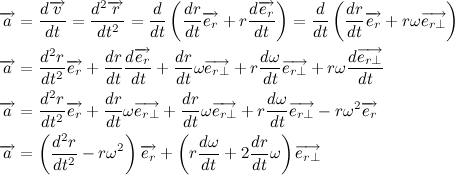
Рассмотрим содержимое второй скобки: 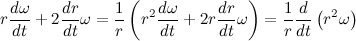
Но мы уже знаем, что 
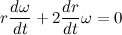
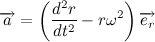
Введем обозначение 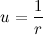
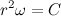
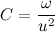
Теперь распишем производную от модуля радиус вектора через С: 
Теперь распишем вторую производную от модуля радиус вектора через С: 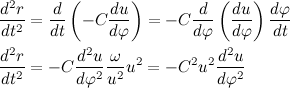
Учитывая полученный результат, перепишем выражение для вектора ускорения: 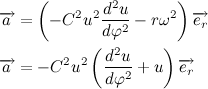
Тогда второй закон Ньютона примет вид: 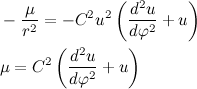
Перепишем полученное дифференциальное уравнение в более привычный вид: 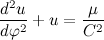
Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.
Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.
Что нам еще предстоит
В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.
Источник