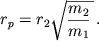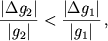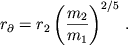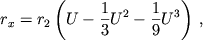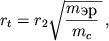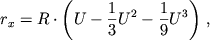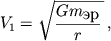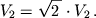Радиус сферы действия луны

Малость радиуса действия тяготения Луны.

Согласно закону всемирного тяготения, тяготение Луны действует вплоть до границ Вселенной. Но самыми значимыми его проявлениями считаются, во-первых, динамическая реакция Земли на Луну, т.е. обращение Земли, в противофазе с обращением Луны, около их общего центра масс, и, во-вторых, лунные приливы в океанах. Однако, правда заключается в том, что тяготение Луны действует лишь в небольшой окололунной области, примерно до 10000 км от лунной поверхности – и, таким образом, оно даже до Земли далеко не достаёт. Поэтому пара Земля-Луна движется весьма своеобразно (см.12), ведь земное тяготение на Луну действует, а лунное тяготение на Землю – нет (см.11). И океанские приливы порождаются отнюдь не тяготением Луны (см.13).

Интересно, что тяготение Луны организовано не по принципу планетарного тяготения. Если Луна имела бы собственную гравитационную воронку, то, при радиолокации Луны узкополосным сигналом, отсутствовал бы вклад в эффект Допплера (как при нашумевшей в своё время радиолокации Венеры группой Котельникова в 1961 году), соответствующий изменению геоцентрического расстояния до Луны из-за того, что её орбита не является круговой. В действительности же этот вклад имеет место. Кстати, опять же: аномально организованное тяготение Луны порождается отнюдь не её веществом. Дело в том, что имеются убийственные свидетельства о том, что Луна представляет собой не сплошное тело, а тонкостенную оболочку – например, по результатам работы сейсмодатчиков на поверхности Луны. Сейсмические события, на которые реагировали эти сейсмодатчики, вызывали и искусственно, для чего на Луну направляли отработанные разгонные ступени ракет. Поразительным было то, что «лунотрясения» длились невероятно долго. Так, после удара о поверхность Луны третьей ступени ракеты Сатурн, использованной для разгона корабля Аполлон-13, «звон» «детектировался в течение более четырёх часов. На Земле, при ударе ракеты на эквивалентном удалении, сигнал длился бы всего несколько минут» [Л6]. Сейсмические колебания с такой высокой добротностью нетипичны для сплошного тела, и, наоборот, они характерны для полого резонатора.

Здесь мы имеем исключительный случай (для всех более чем шестидесяти спутников всех планет Солнечной системы), когда тяготение меньшего по рангу тела действует совместно с тяготением большего по рангу тела – но тяготение меньшего тела на некотором радиусе полностью сходит на нет. Малость этого радиуса проявилась в первых же полётах космических аппаратов в окололунном пространстве. Об этом свидетельствует анализ, во-первых, пролётных окололунных траекторий, и, во-вторых, орбит искусственных спутников Луны – эти орбиты возможны лишь в той области, где лунное тяготение доминирует над земным. Согласно закону всемирного тяготения, такой областью считается т.н. сфера действия Луны, радиус которой составляет 66000 км [Л4]. Но практика окололунных полётов указывает на то, что фактический радиус области лунного тяготения имеет значительно меньшую величину.

Так, советский аппарат «Луна-1», запущенный 2 января 1959 г., впервые в истории космонавтики достиг окрестностей Луны. Планировалось попадание в Луну, которое должна была обеспечить правильность вектора скорости аппарата в конце разгона. Но «из-за ошибки по углу места в 2 о … допущенной при работе наземных радиотехнических средств пеленгации и управления ракетой, двигатель… выключился позже назначенного момента, что и послужило причиной промаха» [ВЕБ17]. Аппарат прошёл на расстоянии около 6000 км от поверхности Луны [Ч1] и, поскольку при разгоне ему была сообщена гиперболическая скорость, вышел за пределы сферы действия Земли, «превратившись… в первую искусственную планету Солнечной системы» [Ч1]. Даже тех скудных данных о параметрах полёта «Луны-1», которые имеются в свободном доступе, достаточно для того, чтобы рассчитать угол поворота траектории аппарата из-за действия лунного тяготения. Расчёт, основанный на концепции сферы действия Луны (с радиусом 66000 км), даёт для угла поворота траектории величину около 11 о . Радиосигналы «Луны-1» принимались в течение ещё суток с небольшим после того, как она разминулась с Луной [Л5], и обнаружение поворота траектории на 11 о не представляло особых сложностей. Но, странным образом, об этом повороте ничего не говорится даже в книге [Л5], где полёт «Луны-1» описан весьма подробно.

Поскольку официальные источники молчат, обратимся к источникам неофициальным. Баллистики, обсчитывавшие первые полёты к Луне, недоумевали: выходило, что поворот оказался значительно меньше того, который был бы по ньютоновской теории. Заказчик ставил задачи со «странными» исходными данными, по расчёту управления лунным спутником. Между тем, малость поворота траектории «Луны-1» могла быть обусловлена малостью радиуса области лунного тяготения, т.е., прохождением аппарата лишь по небольшому участку на её периферии.

Далее, аппарат «Луна-3», запущенный 4 октября 1959 г., впервые произвёл пассивный облёт Луны. Траектория облёта состояла из гиперболического участка в области тяготения Луны и последующего эллиптического разворота, обусловленного тяготением Земли. Из траекторных данных, имеющихся в свободном доступе [Л5], прямо следует малость области тяготения Луны: оценка независимых исследователей для высоты его границы над лунной поверхностью составила 10000 км.

Теперь спрашивается: известны ли случаи, когда искусственный спутник Луны имел орбиту с апоселением (наиболее удалённой точкой от Луны) выше, чем 10000 км от поверхности? В 60-е – 70-е годы ХХ века, максимальную высоту апоселения имел «Лунар Орбитер-5»: 6050 км [К5]. Впоследствии эта цифра была увеличена: американский зонд Clementine (1994) имел высоту апоселения 8300 км, американский зонд Lunar Prospector (1998) – 8500 км [ВЕБ18], а китайский «Чан Э» (2007) – 8600 км [ВЕБ19]. Что касается зонда Kaguya (2007), то для высоты его первого, самого высокого, апоселения Японское космическое агентство назвало цифру 11741 км [ВЕБ20], и её повторили многие информационные агентства. Но эта цифра может быть несколько завышена, поскольку она явилась результатом прогноза, сделанного сразу же после главного тормозного манёвра [ВЕБ20]. Во всяком случае, все названные цифры значительно меньше, чем радиус сферы действия Луны.

Поразительно то, что отечественные и американские специалисты, ещё полвека назад запускавшие первые аппараты к Луне, отлично знают про малость области её тяготения. Но эта информация до сих пор представляет собой важную научную тайну, поэтому современные японские, китайские и европейские аппараты, отправляемые к Луне, нарываются на гравитационные сюрпризы. Известно про два проекта, в которых производились попытки захвата аппарата тяготением Луны на удалениях, значительно больших 10000 км. В обоих случаях официально сообщалось, что захват произошёл – но новоиспечённый спутник Луны оказывался не в состоянии выполнять запланированную научную программу.

Первый из этих двух проектов – полёт японского зонда MUSES-A (Hiten), запущенного в 1990 г. «Во время… первого пролёта Луны предстояло выполнить две задачи: использовать гравитационное поле Луны для увеличения скорости КА и для повышения апогея орбиты, а также отделить от основного КА малый субспутник «Хагоромо», которому предстояло стать искусственным спутником Луны… Отделение «Хагоромо» от базового блока произошло в соответствии с программой полёта в тот момент, когда «Хитен» пролетал на высоте 20 тыс. км от поверхности Луны. Однако собственный передатчик «Хагоромо» вышел из строя, и в центре управления на Земле не удалось получить никаких данных с аппарата и подтвердить его выход на окололунную орбиту. Позже, используя большой оптический телескоп, японским астрономам удалось увидеть, как «Хагоромо» движется по орбите Луны… но как научный аппарат «Хагоромо» был потерян» [ВЕБ21]. Эта официальная версия о выходе «Хагоромо» на окололунную орбиту выглядит неубедительно, поскольку в ней умалчивается о том, удался ли запланированный гравитационный манёвр основного модуля. Более того, в дальнейшем Hiten совершил, как сообщалось, ещё несколько гравитационных манёвров на пролётах вблизи Луны – но, опять же, японцы умалчивали о подробностях. Похоже, хвалиться-то было нечем. Зато известно, что на одиннадцатом пролёте, когда аппарат был переведён на окололунную орбиту, он проходил на расстоянии всего 423 км от поверхности Луны [ВЕБ21]!

Второй же из этих проектов – полёт зонда SMART-1 Европейского космического агентства (ЕКА, ESA). Зонд был выведен ракетой-носителем на околоземную стартовую орбиту в сентябре 2003 г. Затем зонд в течение года с небольшим «раскачивал» орбиту с помощью плазменного двигателя малой тяги, подтягивая апогей к орбите Луны. Планировался захват зонда тяготением Луны при первом же входе в т.н. сферу действия Луны, на удалении от неё около 60000 км. Затем, после снижения на окололунную орбиту, планировалось сделать множество фотографий лунной поверхности. В частности, обещали заснять следы пребывания американских астронавтов на Луне — поэтому миссия была широко прорекламирована.

Специалисты хорошо знали цену этим обещаниям — известно, что Луна чуть не постоянно «скрипит» из-за слабых «лунотрясений», что там имеет место электростатическое «оползание» грунта, и что движение линии терминатора (границы день-ночь) по поверхности Луны сопровождается пыльной бурей. В течение месяца полоса пыльной бури дважды прокатывается по поверхности Луны, и наивно полагать, что от «следов астронавтов» что-то могло сохраниться. Специалисты знали об этом, но помалкивали – как и о том, что лунное тяготение действует на космические аппараты не далее 10000 км от поверхности Луны. Поэтому в ESA не подозревали, что SMART-1 далеко не долетит до области тяготения Луны, и что этот проект обречён на провал.

Теоретически, зонд следовало ввести хотя бы в ближайшую к Земле область сферы действия Луны – с селеноцентрической скоростью, меньшей чем местная круговая – и зонд захватился бы тяготением Луны. Но сразу после того как такой ввод был произведён, что-то пошло «не так». На официальном сайте ESA перестали появляться обновления, оперативно освещавшие полёт SMART-1. После неприлично затянувшейся паузы, ESA задним числом сообщило о том, что зонд был захвачен тяготением Луны, затем, на малой тяге, переведён на низкую полярную орбиту, и даже передал на Землю несколько фотографий участков лунной поверхности. После очередной паузы, эти фотографии были опубликованы. Приглядевшись, специалисты узнали в них снимки тридцатилетней давности, сделанные другими космическими аппаратами. После ещё нескольких месяцев молчания о том, чем занимается SMART-1 в окололунном пространстве, ESA заявило о том, что зонд выполнил свою миссию и будет разбит о поверхность Луны. «SMART-1 спрятал концы в лунную пыль» — издевались информационные агентства. Даже неспециалисты подозревали, что ESA дурачило общественность! О том, как это всё происходило в реальном времени, красноречиво свидетельствует весёлая дискуссия на форуме портала «Новости космонавтики» [ВЕБ22]; доступен также конспект этой дискуссии [ВЕБ23].

Кстати, вывод о лжи ESA можно было сделать сразу после того, как были опубликованы данные [ВЕБ24], описывающие «захват» зонда тяготением Луны. Этих данных достаточно для реконструкции, во-первых, полуэллипса подлёта, по которому зонд двигался в поле тяготения Земли перед тем как, вблизи апогея, войти в сферу действия Луны, и, во-вторых, первого полуэллипса снижения в сфере действия Луны. Легко убедиться в том, что эти два полуэллипса не «сшиваются» друг с другом – а, значит, официальная информация о захвате зонда тяготением Луны и о его дальнейшей судьбе является фальсификацией.

Что же в действительности произошло с зондом SMART-1? По-видимому, при малости области тяготения Луны, зонд просто не вошёл в эту область – и, как ни в чём не бывало, продолжил свой полёт по эллиптической орбите вокруг Земли. Самое разумное, что могли сделать руководители полёта в такой ситуации – это проверить, не «захватится» ли зонд на следующем пролёте через сферу действия Луны. До срока завершения миссии можно было сделать ещё несколько попыток такой проверки. Но чуда не произошло. Чтобы зонд добрался до области лунного тяготения и в самом деле захватился, требовалось ещё поднять апогей и значительно увеличить апогейную скорость. Увы – на малой тяге и с почти израсходованными запасами рабочего вещества – выполнение этой задачи было совершенно нереально. По всей вероятности, зонд до сих пор летает по эллиптической орбите, которая почти дотягивается до орбиты Луны.

А всё потому, что, на расстоянии уже в несколько десятков тысяч километров от Луны, её тяготение, вопреки официальным воззрениям, не действует.

Источник

Радиус сферы действия луны

Впервые за всю историю человечества рукотворный аппарат стал искусственным спутником астероида! Красивая фраза, однако, слова близкая к эллиптической требуют некоторого пояснения.

В учебниках по астрономии хорошо объясняется, как обращаются искусственные спутники по эллиптическим или почти круговым орбитам вокруг сферически симметричных тел, к числу которых можно отнести планеты и, в частности, нашу Землю. Однако взгляните на Эрос эту картофелеобразную глыбу размером 33*13*13 км. Гравитационное поле тела столь неправильной формы является весьма сложным, и чем ближе приближался к нему NEAR, тем сложнее становилась задача по его управлению. Совершив один виток вокруг Эроса, аппарат никогда не возвращался в точку его начала. Хуже того, не сохранялась даже плоскость орбиты зонда. Когда в коротких пресс-релизах сообщалось, что NEAR перешел на новую круговую орбиту, надо было видеть, какие замысловатые фигуры выписывал он в действительности!

Просто счастье, что в наше время на помощь людям пришли компьютеры. Сложная задача удержания аппарата на нужной орбите выполнялась программами автоматически. Если бы это делал человек, то ему можно было бы смело ставить памятник. Судите сами: во-первых, орбита аппарата никогда не должна была отклоняться более чем на 30 o от перпендикуляра к линии Солнце Эрос. Это требование определялось дешевой конструкцией аппарата. Панели солнечных батарей должны были всегда смотреть на Солнце (иначе смерть аппарата наступила бы в течение часа), главная антенна в момент передачи данных на Землю, а приборы во время их сбора на астероид. При этом все приборы, антенны и панели солнечных батарей были закреплены на NEAR неподвижно! 16 часов в сутки аппарату отводилось на сбор информации об астероиде и 8 на передачу данных через главную антенну на Землю [2].

Во-вторых, в большинстве экспериментов необходимы были как можно более низкие орбиты. А это, в свою очередь, требовало и более частых маневров, и большего расхода топлива. Тем ученым, которые производили картографирование Эроса, нужно было последовательно облететь на небольшой высоте все участки астероида, а тем из них, кто занимался получением изображений, вдобавок нужны были еще и различные условия освещения. Прибавьте к этому то, что на Эросе тоже существуют свои сезоны и полярные ночи. К примеру, южное полушарие открыло Солнцу свои просторы только к сентябрю 2000 года. Как в этих условиях угодить всем?

Помимо прочего, нужно было учесть еще и чисто технические требования к стабильности орбиты. В противном случае, потеряв связь с NEAR всего на неделю, можно было больше никогда его не услышать. И, наконец, ни при каких обстоятельствах нельзя было загонять аппарат в тень астероида. Он бы погиб там без Солнца! К счастью за окном компьютерный век, поэтому все эти задачи были возложены на электронику, люди же спокойно решали свои.

5.2. Орбиты небесных тел

Орбиты небесных тел траектории, по которым движутся в космическом пространстве Солнце, звезды, планеты, кометы, а также искусственные космические аппараты (искусственные спутники Земли, Луны и других планет, межпланетные станции и т.п.). Однако для искусственных космических аппаратов термин орбита применяют лишь к тем участкам их траекторий, на которых они движутся с выключенной двигательной установкой (так называемые пассивные участки траектории).

Формы орбит и скорости, с которыми движутся по ним небесные тела, определяются главным образом силой всемирного тяготения. При исследовании движения небесных тел в большинстве случаев допустимо не принимать во внимание их форму и строение, то есть считать их материальными точками. Такое упрощение возможно потому, что расстояние между телами обычно во много раз больше их размеров. Считая небесные материальными точками, мы можем при исследовании движения непосредственно применять закон всемирного тяготения. Кроме того, во многих случаях можно ограничиться рассмотрением движением только двух притягивающихся тел, пренебрегая влиянием других. Так, например, при изучении движения планеты вкруг Солнца можно с известной точностью предполагать, что планета движется толь под действием силы солнечного тяготения. Точно также при приближенном изучении движения искусственного спутника планеты можно принять во внимание лишь тяготения своей планеты, пренебрегая не только притяжением других планет, но и солнечной.

Указанные упрощения приводят к так называемой задаче двух тел. Одно из решений этой задачи было дано И. Кеплером, полное решение задачи было получено И. Ньютоном. Ньютон доказал, что одна из притягивающихся материальных точек обращается вокруг другой по орбите, имеющей форму эллипса (или окружности, которая является частным случаем эллипса), параболы или гиперболы. В фокусе этой кривой находится вторая точка.

Форма орбиты зависит от масс рассматриваемых тел, от расстояния между ними и от скорости, с которой одно тело движется относительно другого. Если тело массой m₁ (кг) находится на расстоянии r (м) от тела массой m₀ (кг) и движется в этот момент времени со скоростью V (м/с), то вид орбиты определяется величиной h = V 2 -2f(m₀+ m₁)/ r.

Постоянное тяготение G = 6.673 10 -11 м 3 кг -1 c -2 . Если h меньше 0, то тело m₁ движется относительно тела m₀ по эллиптической орбите; Если h равно 0 — по параболической орбите; Если h больше 0, то тело m₁ движется относительно тела m₀ по гиперболической орбите [6].

Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно, начав движение вблизи поверхности Земли, преодолело земное притяжение и навсегда покинуло Землю по параболической орбите, называется второй космической скоростью. Она равна 11.2 км/с. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна 7.91 км/с.

По эллиптическим орбитам движется большинство тел солнечной системы. Только некоторые малые тела Солнечной системы кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полета наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.

Ориентация орбиты в пространстве, ее размеры и форма, а также положение небесного тела на орбите определяются шестью величинами, называемыми элементами орбиты. Некоторые характерные точки орбит небесных светил имеют собственные названия. Так, ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца, называется перигелием, а наиболее удаленная от него точка эллиптической орбиты афелием. Если рассматривается движение тела относительно Земли, то ближайшая к Земле точка орбиты называется перигеем, а самая далекая апогеем. В более общих задачах, когда под притягивающим центром можно подразумевать разные небесные тела, употребляют названия: перицентр (ближайшая к центру точка орбиты) и апоцентр (наиболее удаленная от центра точка орбиты).

Случай взаимодействия только двух небесных тел является простейшим почти не наблюдается (хотя и имеется много случаев, когда притяжением третьего, четвертого и т.д. тел можно пренебречь). В действительности все обстоит намного сложнее: на каждое тело действуют многие силы. Планеты в своем движении притягиваются не только к Солнцу, но и друг к другу. В звездных скоплениях каждая звезда притягивается всеми остальными. На движение искусственных спутников Земли оказывают влияние силы, вызываемые несферичностью фигуры Земли и сопротивлением земной атмосферы, притяжение Луны и Солнца. Эти дополнительные силы называют возмущающими, а эффекты, которые они вызывают в движении небесных тел, — возмущениями. Из-за возмущений орбиты небесных тел непрерывно медленно изменяются [6].

Исследованием движения небесных тел с учетом возмущающих сил занимается раздел астрономии небесная механика. Методы, разработанные в небесной механике, позволяют очень точно на много лет вперед определить положение любых тел Солнечной системы. Более сложные методы вычислений используются при исследовании движения искусственных небесных тел. Точное решение этих задач в аналитическом виде (то есть в виде формул) получить крайне сложно. Поэтому используются методы численного решения уравнений движения с применением быстродействующих электронных вычислительных машин. При таких вычислениях пользуются понятием сферы действия планеты. Сферой действия называют область околопланетного пространства, в которой при расчетах возмущенного движения тела (КА) удобно в качестве центрального тела считать не Солнце, а эту планету. В этом случае расчеты упрощаются вследствие того, что внутри сферы действия возмущающее влияние притяжения Солнца в сравнении с притяжением планеты меньше, чем возмущающее от планеты в сравнении с притяжением Солнца. Но нужно помнить, что и внутри сферы действия и за ее пределами всюду на тело действуют силы притяжения и Солнца, и планеты и других тел, хотя и в разной степени.

Радиус сферы действия зависит от расстояния между Солнцем и планетой. Орбиты небесных тел внутри сферы действия можно рассчитать на основе задачи двух тел. Если небесное тело покидает планету, то движение этого тела внутри сферы действия происходит по гиперболической орбите. Радиус сферы действия Земли равен около 1 млн. км; сфера действия Луны по отношению к Земле имеет радиус около 63 тысяч километров.

Метод определения орбиты небесного тела с использованием понятия сферы действия один из способов приближенного определения орбит. Зная приближенные величины элементов орбиты, можно с помощью других методов получить более точные значения элементов орбиты. Такое поэтапное улучшение определяемой орбиты является типичным приемом, позволяющим вычислить параметры орбиты с высокой точностью. В настоящее время круг задач по определению орбит значительно расширился, что объясняется бурным развитием ракетной и космической техники [9].

5.3. Упрощенная постановка задачи трех тел

Задача движения КА в гравитационном поле двух небесных тел является достаточно сложным и ее обычно исследуют численными методами. В ряде случаев оказывается допустимым упрощение этой задачи путем разделения пространства на две области, в каждой из которых учитывается притяжение только одного небесного тела. Тогда внутри каждой области пространства движение КА будет описываться известными интегралами задачи двух тел. На границы перехода из одной области в другую необходимо соответствующим образом пересчитать вектор скорости и радиус-вектор с учетом замены центрального тела.

Разделение пространства на две области можно осуществлять на основе различных допущений, которые определяют границу. В задачах небесной механики, как правило, одно небесное тело имеет массу существенно большую, чем второе. Например, Земля и Луна, Солнце и Земля или любая другая планета. Поэтому область, где предполагается движение КА по коническому сечению, в фокусе которого находится меньше притягивающее тело, занимает только небольшую часть пространства вблизи этого тела. Во всем оставшемся пространстве предполагается движение КА по коническому сечению, в фокусе которого находится большее притягивающее тело. Рассмотрим некоторые принципы разделения пространства на две области.

5.4. Сфера притяжения

Совокупность точек пространства, в котором меньшее небесное тело m₂ притягивает КА сильнее, чем большее тело m₁, называют областью притяжения или сферой притяжения меньшего тела относительно большего. Здесь по поводу понятия сфера справедливо замечание, сделанное для сферы действия [7].

Пусть m₁ масса и обозначение большого притягивающего тела, m₂ масса и обозначение меньшего притягивающего тела, m₃ масса и обозначение КА.

Их взаимное расположение определяется радиусами-векторами r₂ и r ₃, которые соединяют m₁ соответственно с m₂ и m₃.

Граница области притяжения определяется условием: |g₁|=|g₂|, где g₁ — гравитационное ускорение, сообщаемое КА большим небесным телом, а g₂ — гравитационное ускорение, сообщаемое КА меньшим небесным телом.

Радиус сферы притяжения рассчитывается по формуле:

5.5. Сферы действия

Областью действия, или сферой действия, меньшего тела m₂ относительно большего тела m₁ называют область пространства, в которой выполняется условие:

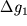
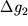
где g₁ — ускорение, которое получает КА при движении в центральном поле тело m₁, — возмущающее ускорение, которое получает КА из-за наличия притягивающего тела m₂, g₂ — ускорение, которое получает КА при движении в центральном поле тело m₂, — возмущающее ускорение, которое получает КА из-за наличия притягивающего тела m₁.

Заметим, что при введении этого понятия под словом сфера сначала имеем в виду не геометрическое место точек, одинаково удаленных от центра, а область преимущественного влияния меньшего тела на движение КА, хотя граница этой области действительно близка к сфере.

Внутри сферы действия меньшее тело рассматривают в качестве центрального, а большее тело как возмущающее. Вне сферы действия за центральное принимают большее тело, а возмущающее меньшее. В ряде задач небесной механики оказывается возможным пренебречь в первом приближении влиянием на траекторию КА большего тела внутри сферы действия и меньшего тела вне этой сферы. Тогда внутри сферы действия движение КА будет происходить в центральном поле, создаваемом меньшим телом, а вне сферы действия — в центральном поле, создаваемом большим телом. Границу области (сферы) действие меньшего тела относительно большего определяют по формуле:

5.6. Сфера Хилла

Сферой Хилла называют замкнутую область пространства с центром в притягивающей точке m₂, двигаясь внутри которой тело m₃ всегда будет оставаться спутником тела m₂.

Сфера Хилла названа так по имени американского астронома Дж. В. Хилла, который в своих исследованиях движения Луны (1877 г.) впервые обратил внимание на существование областей пространства, куда не может попасть тело бесконечно малой массы, находящееся в гравитационном поле двух притягивающих тел.

Поверхность сферы Хилла может рассматриваться как теоретическая граница существования спутников тела m₂. Например, радиус селеноцентрической сферы Хилла в системе Земля Луна ИСЛ составляет r = 0.00039 а.е. = 58050 км, а в системе Солнце Луна ИСЛ r = 0.00234 а.е. = 344800 км.

Радиус сферы Хилла вычисляется по формуле:

5.7. Расчеты и выводы

В предыдущих разделах были описаны сфера тяготения, сфера действия и сфера Хилла. Теперь определим скорость КА NEAR и максимальное расстояние от астероида, на котором КА сможет выйти на орбиту вокруг Эроса.

В расчетах будем считать, что масса Солнца равна 1.9734*10 30 кг, масса Эроса 6.687*10 15 кг. Тогда радиус сферы тяготения вычисляется по формуле:

радиус сферы действия по формуле:

а радиус сферы Хилла по формуле:

где R — расстояние от Эроса до Солнца,

Т.к. все радиусы зависят от расстояния между Солнцем и астероидом, то вычислим их для трех разных случаев: перигелия (П, минимальное расстояние от Солнца равно 169 млн. км), афелия (А, максимальное расстояние от Солнца равно 266 млн. км.), для среднего расстояния (Ср, 218 млн. км.).

Первая космическая скорость вычисляется по формуле:

где G — гравитационная постоянная (G = 6.6732*10 -11 Н м 2 /кг 2 ), r — расстояние до астероида; вторая космическая скорость равна:

Вычислим первую и вторую космические скорости для каждого значения радиуса сфер. Результаты занесем в табл.1, табл.2, табл.3.

Табл. 1. Радиусы сферы тяготения для разных расстояний Эроса от Солнца.

Источник