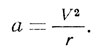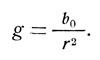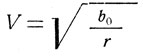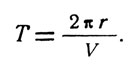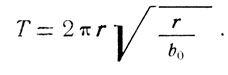Радиус круговой орбиты луны движущейся вокруг земли

Почему Луна вращается вокруг Земли по круговой орбите?

Луна движется вокруг Земли по орбите, близкой к круговой, потому что она – искусственный объект, а параметры его орбиты были заданы теми, кто доставил этот объект в Солнечную систему и заставил вращаться вокруг нашей планеты – Мидгард-земли. Я сейчас вам всё объясню подробнее.

Мнение «учёных» о том, что Луна является естественным спутником Земли и появилась возле неё в результате некой космической катастрофы, ничем не обосновано и не подтверждено. А попытка навязать эту гипотезу Человечеству без доказательств в качестве очередного постулата, свидетельствует о том, что это заблуждение «учёных» не является случайным.

Любой образованный человек в состоянии легко указать на несколько явных противоречий в существующей ортодоксальной «теории» появления и движения Луны.

Во-первых, не бывает таких космических катастроф, после которых первый результат миллиарды лет вращается вокруг второго по круговой орбите. Результатом любой катастрофы является хаос, а не аккуратное вращение планет друг возле дружки.

Во-вторых, не бывает таких хитрых катастроф, после которых вращение Луны вокруг Земли было бы синхронизировано таким образом с её вращением вокруг своей оси, чтобы Луна всё время была повёрнута к нам одной и той же стороной. Процесс такой синхронизации наверняка очень сложный, и у природы нет, и не может быть причин создавать его естественным образом.

В-третьих, то, что Луна является искусственным объектом, уже давно известно и даже доказано в многочисленных источниках.

И вот теперь – самое интересное! Сразу хочу сказать вам, что Луна не притягивается Землёй, потому Закона «Всемирного тяготения» не существует в природе! Необходимые доказательства этого утверждения я уже давно собрал в статьях «Бирюльки и фитюльки тяготения», «Зачем лжёт президент РАН Сергеев?» и многих других.

Луна не просто так болтается в пространстве, а находится внутри искривления (неоднородности) пространства, как в большой «тарелке», из которой она не может выбраться. В центре этой «тарелки» размещён локальный источник гравитации – резкий перепад параметров пространства (перепад мерности). Источник гравитации Луны находится в районе центра Земли. Внутри своей «тарелки» Луна вращается вокруг Земли как будто по краю «тарелки». А вместе со своей «тарелкой» (неоднородностью пространства) она вместе с Землёй вращается вокруг Солнца. На рисунке это хорошо видно.

Первоматерии, циркулирующие в пространстве во всех направлениях, всегда движутся к источнику гравитации и своим движением «стараются» прижимать Луну к источнику – фактически к Земле. Но, благодаря тому, что потоки первоматерий действуют на неё со всех сторон, Луна не падает на Землю, а находится на орбите, определяемой формой неоднородности пространства («тарелки») и параметрами движения по этой неоднородности.

Земля находится в своей неоднородности пространства (в своей «тарелке»), она в ней и была синтезирована природой в своё время. Земная «тарелка» значительно больше лунной (на рисунке – голубая), в её центре находится наше Солнце. На Землю гравитация действует точно так же, как и на Луну. Поэтому Земля не падает на Солнце, а вращается по орбите, заданной нашими предками, когда они упорядочивали Солнечную систему перед колонизацией. Земля вращается вокруг Солнца как бы по «ободку», всё время находясь внутри своей «тарелки».

Точно так же, как и Земля, все остальные планеты Солнечной системы находятся в своих неоднородностях пространства («тарелках»), и вращаются вокруг Солнца по орбитам, определяемым формами и размерами их «тарелок».

Солнце также находится в своей неоднородности («тарелке»), и также под действием уже своей локальной гравитации вращается вокруг центра Галактики вместе со всей своей гирляндой планет, спутников, метеоритов и прочих космических объектов.

Резюмируя, можно уверенно сказать следующее: Луна вращается вокруг Земли по орбите, определяемой формой пространственной «тарелки», ограничивающей ещё движение в Космосе. Параметры «тарелки» были установлены нашими предками, когда они упорядочивали Солнечную систему перед колонизацией и делали вокруг Земли «гравитационный оазис» для обеспечения ускоренного эволюционного развития всех, кто находился на Земле.

Находиться внутри «тарелки» Луну заставляет гравитация – потоки первоматерий, со всех сторон прижимающие Луну к источнику гравитации. Она не падает на Землю, потому что находится в равновесии, ведь потоки давят со всех сторон.

Природа вообще значительно больше и интереснее той глупости, что десятилетиями рассказывают нам полуграмотные «учёные». И, кроме того, в природе не бывает упорядоченности, т.е. не бывает никаких «круговых орбит», никакой синхронизации между планетами, никаких «плоскостей эклиптики» и ничего другого, подобного этому.

Дикая природа – это хаос! И если вы где-нибудь заметили малейшую упорядоченность, то будьте уверены, что это результат действия весьма разумных существ!

Тайны Луны. Секреты, связанные с Луной

Луна. 7 самых загадочных случаев

Источник

Радиус круговой орбиты луны движущейся вокруг земли

Я написал пару недель назад о том, что если посмотреть на то, как Луна движется вокруг Солнца, то это не такие петли, как можно наивно представить, а выпуклая (!) кривая. «Полезная метафора: представьте себе две гоночные машины на длинной круговой трассе. Первая обгоняет вторую справа и встраивается перед ней, тут же вторая обгоняет первую справа и возвращается влево, и так далее. Вот так Земля и Луна «обгоняют» друг друга на трассе вокруг Солнца».

Но мне все равно было трудно представить, как это все-таки выглядит. Если представить себе маршруты этих двух машин, то кажется, что при переходе во внутренний ряд, а потом обратно во внешний, не получается никак выпуклая траектория, скорее длинные волны такие.

Проблема в том, что это трудно убедительно нарисовать. Радиус орбиты вокруг Солнца столь огромен по сравнению с радиусом орбиты вокруг Земли, что если показать весь большую орбиту, то пути Земли и Луны по ней совпадут, не различить на экране или на бумаге. А траектория выпуклая именно потому, что разница в радиусах такая, если бы она была меньше, были бы как раз «петли».

В общем, я написал симуляцию, которая дает подвигать параметры и посмотреть, как оно выходит. По умолчанию там подобраны значения, которые показывают, как Луна может двигаться по очевидно выпуклой траектории (красная кривая) и одновременно вращаться вокруг Земли (голубая кривая). Можно двигать самым последним контролем и смотреть, как орбита развивается во времени.

Это не совсем честные параметры: радиус орбиты Луны увеличен в 10 раз (a=10), а кол-во лунных месяцев в году уменьшено в 2 раза (m=6), для наглядности. Можно поменять на честные, но тогда орбиты сливаются, как написано выше. Внизу страницы есть текстовое объяснение.

Это упрощенная модель, конечно — окружности, а не эллипсы, одна и та же плоскость вращения — но она очень близка к реальным орбитам. Если R радиус орбиты Земли вокруг Солнца, A радиус орбиты Луны вокруг Земли, M количество лунных месяцев в году (т.е. отношение периодов вращения), то приблизительное условие для того, чтобы орбита Луны была выпуклой — это R/A >= M^2. Например, в реальности R/A=400, M=13 лунных месяцев, M^2=169. В примере, выставленном по умолчанию на странице, R/A=40, M^2=36.

Источник

Радиус круговой орбиты луны движущейся вокруг земли

Круговая орбита спутника

Известно, что движение достаточно широкого класса космических аппаратов происходит по орбитам, близким к круговым. Круговое движение — наиболее простое и его закономерности имеют большую наглядность. Прежде чем начать изучение кругового движения, необходимо установить условия, при которых оно образуется.

Чтобы получить представление о круговом движении, достаточно проделать следующий простой опыт. Возьмите кусок шпагата и к одному из концов его привяжите небольшой груз. Затем, взяв в руку другой конец шпагата, раскрутите грузик вокруг себя. Нить вытянется, и грузик будет описывать окружность. Это — простейшая модель искусственного спутника Земли. Здесь грузик выполняет роль летящего космического аппарата, натяжение нити — силу притяжения Земли. Когда грузик вращается вокруг вас, то возникает хорошо известная центробежная сила, которая стремится разорвать нить. Удерживая рукой нить, вы не даете грузику возможности улететь от вас и заставляете вращаться по кругу. Нечто аналогичное происходит и в космическом масштабе. Когда космический аппарат движется относительно Земли, то силы ее тяготения искривляют траекторию движения, вследствие чего возникают центробежные силы, препятствующие искривлению траектории движения и направленные в сторону, противоположную направлению притяжения Земли. Круговая орбита образуется именно тогда, когда центробежные силы полностью уравновешены силой притяжения. Переходя от сил притяжения к ускорениям, как это было выполнено выше, мы можем уравнение движения космического аппарата записать в следующей символической форме:

Как известно, величины центробежной силы или центробежного ускорения зависят от скорости полета и радиуса орбиты: чем выше скорость движения и меньше радиус орбиты, тем эти величины больше. Океанский теплоход, плывущий по океану, описывает круговую орбиту, равную радиусу Земли. Возникающие при этом центробежные силы стараются оторвать его от Земли. Однако эти силы достаточно малы, так как мала скорость движения теплохода. Так, если теплоход плывет со скоростью 30 узлов, то действующая на него центробежная сила составит 0,0003% его веса. При водоизмещении теплохода 100000 тонн она достигнет 300 кг, т. е. равна весу трех пассажиров и еще некоторого багажа. Поэтому, если вас уверяют, что отплывающий в г. Сочи теплоход загружен полностью, то вы, вооружившись этими данными, можете смело рассчитывать на посадку по крайней мере еще трех человек.

Величины центробежной силы становятся заметнее при полете на сверхзвуковом самолете. Самолет ТУ-144 летает со скоростью 2500 км/час. При этой скорости величина центробежной силы достигает одного процента от веса самолета. Если положить вес самолета на Земле равным 150 т, то в «горизонтальном полете» он уменьшится на полторы тонны, т. е. он может нести дополнительно 15 пассажиров.

Еще большее значение центробежная сила имеет при полете гиперзвуковых самолетов. Так, при скорости полета, равной 15 скоростям звука (около 5 км/сек), вес самолета уменьшается на 40%.

Эти примеры, в частности, свидетельствуют, что увеличение скорости полета не просто количественный рост, а качественно новый результат, отражающийся на весовом балансе летательного аппарата. Именно эти соображения могут наталкивать пас на мысль о целесообразности увеличения скоростей полета.

Но вернемся к полету космического аппарата. Пусть по окончании работы его двигателей он оказался на высоте 200 км, имея скорость 7,75 км/сек параллельно поверхности Земли. Возникающая при этом центробежная сила будет составлять 99% от веса аппарата, а неуравновешенным останется только 1% его веса. За счет воздействия этой небольшой силы космический аппарат начнет медленно приближаться к Земле и пролетит многие тысячи километров, прежде чем упадет на Землю. Но стоит только увеличить скорость полета до 7,791 км/сек, как центробежная сила сравняется с весом аппарата и он начнет летать вокруг Земли. Такую скорость полета баллистики называют первой космической скоростью.

Ранее уже говорилось о том, что скорость есть принципиально необходимое условие осуществления космического полета. Приведенные простые рассуждения со всей очевидностью показали, что существуют строго определенные жесткие границы скорости, ниже которых существование космического аппарата не обеспечивается. В качестве такой границы принимается первая космическая скорость — это скорость, которой должен обладать космический аппарат, чтобы стать искусственным спутником планеты и двигаться вокруг нее по круговой орбите. Иногда эту скорость называют также круговой.

Чтобы получить математическую зависимость для круговой скорости, обратимся к уравнению движения. Как известно, если какое-либо тело движется со скоростью V по орбите радиуса r, то при этом возникает центростремительное ускорение

В соответствии с приведенным уравнением движения оно должно быть равно ускорению, обусловленному притяжением Земли, для которого в первом разделе получено следующее выражение (формула 2):

Приравнивая эти ускорения, получим следующее простое соотношение для расчета первой космической скорости:

Напомним, что здесь r — расстояние от центра планеты до космического аппарата (радиус орбиты), b₀ — гравитационный параметр планеты, значение которого можно взять из табл. 1.

Первая космическая скорость — это не мировая константа (т. е. постоянная величина), неизменная при всех условиях, как остается, например, неизменным число , равное 3,14. Как легко видеть из формулы (3), она зависит от массы планеты, относительно которой производится полет (посредством величины числа b₀) и радиуса орбиты (или высоты полета над планетой).

Напомним основные допущения, которые были приняты при выводе формулы для первой космической скорости:

а) гравитационное поле планеты является центральным, т. е. планета является сферой с однородным распределением ее плотности;

б) притяжение других планет, сопротивление атмосферы, световое давление, а также действие других сил отсутствует;

в) ускорение силы притяжения планеты направлено всегда к ее центру и его абсолютная величина определяется на основании закона тяготения Ньютона;

г) масса космического аппарата исчезающе мала по сравнению с массой планеты.

Понятно, что перечисленные условия никогда (именно никогда!) не выполняются в реальных космических полетах. Фактические условия полета, например, на орбитах спутника Земли, могут лишь в какой-то мере приближаться к идеализированным представлениям и поэтому к полученным по этой теории количественным результатам следует относиться критически и с большой осторожностью. Значения космических скоростей должны рассматриваться как некоторые абстрактные величины, не отвечающие своему содержанию при перенесении их на реальные условия полета. Действительно, вы можете легко рассчитать первую космическую скорость полета на малой высоте относительно поверхности Земли. Но в нижних слоях атмосферы сопротивление воздуха, действующее на двигающийся с космической скоростью аппарат, достигло бы громадной величины, составляющей несколько тысяч тонн. И никакой двигатель не в состоянии преодолеть эту силу. Значит, существование космического аппарата здесь совершенно исключено. На высоте 32 км плотность воздуха в 100 раз меньше, чем у поверхности Земли, и сила сопротивления снизится до десятков тонн. Но это также большая величина. На высоте 100 км плотность воздуха уменьшается уже в 1 000000 раз, но и там при космических скоростях полета сила сопротивления будет измеряться килограммами. Этим также пренебречь нельзя. Значит, чтобы иметь возможность проводить некоторую аналогию между первой космической скоростью и реальными условиями полета, необходимо забираться все выше и выше. Но здесь, наряду с уменьшением сопротивления атмосферы, все с возрастающим эффектом начнет сказываться притяжение Луны, Солнца и других планет. Поэтому область допустимого определения первой космической скорости лежит не слишком близко к Земле, но и не очень далеко от нее. Обычно ее распространяют от высот 200 км до нескольких десятков тысяч километров. Но и в этом случае определение допустимо только на относительно небольших участках полета. С течением времени отличия кругового движения от реального будут возрастать и поэтому теория кругового движения в конце концов приведет к качественно и количественно неверным результатам. И когда мы будем пользоваться этой теорией, то всегда будем иметь в виду, что она соответствует полету космического аппарата только приближенно и на малых отрезках времени. В зависимости от требований к точности прогноза и высоты начальной орбиты эти отрезки времени могут исчисляться от нескольких часов до суток.

Необходимо также отметить, что круговая скорость для данной высоты полета является однозначной и строго определенной величиной. Даже самое незначительное изменение скорости деформирует орбиту и она перестает быть круговой, хотя геометрически это отличие может быть и небольшим. Точно так же малые возмущающие ускорения могут незначительно изменять круговую орбиту, и в этих случаях говорят, что движение происходит по почти круговым орбитам.

Проследим характер изменения первой космической скорости с подъемом на высоту. Как известно, в соответствии с законом всемирного тяготения все тела притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Поэтому по мере подъема на высоту сила, с которой тело притягивается к Земле, будет уменьшаться. Например, на высоте 200 км вес тела на 6% меньше, чем у поверхности Земли, на высоте 800 км уменьшение веса достигает уже 20%, а на высоте 2640 км тело становится в 2 раза легче. По этой причине космическому аппарату после подъема на некоторую высоту уже требуется меньшая скорость, чтобы выйти на круговую орбиту. Значит, чем выше поднят аппарат, тем меньше величина скорости, необходимой для полета по круговой орбите. Например, если спутник поднят на высоту, равную трем радиусам Земли (напомним: радиус Земли равен около 6371 км), то первая космическая скорость окажется в два раза меньшей, чем у поверхности Земли, составит всего 3,956 км/сек. Луна — естественный спутник Земли и движется вокруг Земли по почти круговой орбите со средним радиусом 384 тыс. км. На этом расстоянии от Земли первая космическая скорость составляет 1,02 км/сек и примерно с такой скоростью движется Луна относительно Земли.

Таким образом, мы рассмотрели два элемента круговых орбит — радиус и скорость полета. В случае кругового движения эти элементы зависят друг от друга. Задавшись одним из них, с помощью соотношения (3) мы можем определить значение второго элемента. Значит, круговую орбиту можно однозначно характеризовать только одним элементом либо величиной скорости, либо ее радиусом. С этими названными элементами находится в непосредственной связи третий элемент — период обращения. Периодом обращения космического аппарата, движущегося по круговой орбите, называется промежуток времени, необходимый для совершения одного витка. Так как длина одного витка равна 2 л г, то, поделив ее на скорость полета, получим формулу для расчета периода обращения

Если вместо скорости подставить ее значения из формулы (3), то получим явную зависимость периода обращения от радиуса орбиты и массы планеты:

Отсюда следует, что период обращения тоже является однозначной функцией радиуса круговой орбиты: задавшись радиусом, по формуле (4) находим период. Можно решить и обратную задачу: задавшись периодом обращения, определить соответствующий ему радиус орбиты.

Основные характеристики кругового движения — скорость полета и период обращения. При изучении характеристик круговых орбит можно отметить, в частности, один любопытный факт. Пусть высоты орбит спутников Земли и Луны равны 200 км, т. е. их радиусы орбит составляют соответственно 6571 км и 1938 км. Однако, несмотря на то, что радиус орбиты спутника Луны более чем в три раза меньше радиуса орбиты спутника Земли, его период имеет большую величину и составляет примерно 2 часа 7 минут, тогда как у спутника Земли он равен 1 час 28 минут. Значит, при равной высоте спутник Земли вращается с большей скоростью, чем спутник Луны. Это объясняется тем, что масса Луны примерно в 80 раз меньше массы Земли.

Источник