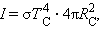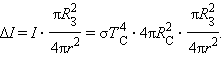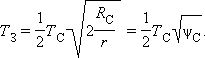Солнечная постоянная $C$, по определению, есть величина, равная:

где $W$ — энергия, излучаемая Солнцем за время $t$; $S = 4 \pi r^<2>$ — площадь сферической поверхности, радиуса $r$ который равен среднему расстоянию Земли от Солнца.
Энергию, излучаемую Солнцем за время $t$ выразим следующим образом

где $R_$ — излучательность Солнца, т.е. энергия, которую оно излучает в единицу времени единицей поверхности; $S_<0>$ — площадь поверхности Солнца.
Подставляя выражение (2) в формулу (1) получаем

Выразим площадь поверхности Солнца $S_<0>$ через диаметр $d$ по формуле: $S_ <0>= \pi d^<2>$. Тогда,

Обратимся к рисунку. Так как угол $\theta$ мал, то можно записать, что $d = r \theta$, где угол $\theta$ выражаем в радианах. С учетом этого формула (3) принимает вид:

Отсюда определяем излучательность Солнца

Температуру поверхности Солнца определим воспользовавшись законом Стефана- Больцмана, полагая, что Солнце излучает как абсолютно черное тело.
Согласно закону Стефана — Больцмана излучательность абсолютно черного тела

где $\sigma$ — постоянная Стефана — Больцмана ($\sigma = 5,67 \cdot 10^ <-8>\frac<Вт> <м^<2>\cdot К^ <4>>$ ). Отсюда

Подставляя в это выражение значение $\sigma$ и найденное выше значение $R_$ и произведем вычисления, получим:

Источник

Приняв что солнце излучает как абсолютно черное тело найти

Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:

1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.

2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.

3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2

4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.

5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.

6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь

8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.

9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.

10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.

11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0

12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.

13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.

14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.

Источник

Задачи с решениями

Принимая, что Солнце излучает как абсолютно черное тело с температурой поверхности , оцените среднюю температуру земной поверхности в предположении, что Земля также является абсолютно черным телом, а роль тепловых процессов внутри Земли пренебрежимо мала. Угловой диаметр Солнца, видимый с Земли, примите равным .

В пренебрежении процессами, идущими в недрах Земли, тепловой баланс Земли определяется поглощением энергии солнечного излучения и собственным излучением в пространство. Полный поток энергии , излучаемой Солнцем по всем направлениям, в соответствии с законом Стефана–Больцмана равен

где – постоянная Стефана–Больцмана, – радиус Солнца. Часть полного потока падает на поверхность Земли и поглощается:

Здесь – радиус Земли, – расстояние от Земли до Солнца.

Такой же поток энергии Земля должна излучать в пространство, иначе ее температура не будет оставаться постоянной. Приравнивая поток излучаемой Землей энергии 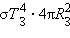и поглощаемый ею поток энергии , получим:

Из этого выражения видно, что для определения нужно знать только температуру поверхности Солнца и его угловой диаметр 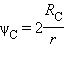. Числовой расчет дает значение . Этот результат весьма близок к реальному значению средней температуры поверхности Земли.

Источник

солнце излучает как абсолютно черное тело найти плотность потока излучения вблизи земли за пределами ее атмосферы

Похожую задачу смотри ТУТ

Закон Стефана-Больцмана для излучения абсолютно черного тела пишем
☛ R=σ*T⁴ ①

Закон смещения Вина пишем
☛ λ(max)=b/T ②

И еще надо понимать физический смысл энергетической светимости R. Он вытекает из размерности [R]=Дж/(м²*с) . Получается, что R — это энергия, излучаемая за 1 секунду одним квадратным метром нагретой площади поверхности Солнца, т. е.

Подставляешь площадь поверхности Солнца S=4*π*r², получаешь полную энергию, излучаемую Солнцем за какое-то время t (например, t=60 секунд) :

Пришла пора расчеты проделать.
Известно:
λ(max)=470нм=4,70*10⁻⁷ м
r=6,95*10⁸ м
b=0,0029 — постоянная Вина
σ=5,67*10⁻⁸ — постоянная Стефана-Больцмана

Из формулы ② определяешь температуру T, потом по формуле ① считаешь энергетическую светимость R. Наконец, из ③ находишь энергию Е (время t можешь взять каким угодно, например, конкретно t=60 секунд) .

Ну, и теперь вопрос: куда девается вся эта энергия Е? А уходит она от Солнца прочь в виде лучей. Лучи как раз и переносят энергию через пустоту космоса.
Вся энергия, что испустило Солнце за 60 секунд, распространяется от Солнца в радиальном направлении и пересекает поверхность сферы с радиусом
Rорб. земли = 1,5*10¹¹ м.

Поделишь энергию Е на время t=60 секунд и на площадь сферы радиусом 1,5*10¹¹ м, получишь ответ, т. е. плотность потока излучения вблизи Земли (это все по определению, так как плотность потока энергии — это энгергия, поделенная на время и поделенная на площадь поверхности, которую эта энергия пересекает) .

Всего доброго, успехов в учебе. ☺

ЗЫ. Вычисления в этой задаче очень противные.
Должен получиться примерно такой ответ:
1367 Вт/м² — так называемая Солнечная постоянная

Источник

Приняв что солнце излучает как абсолютно черное тело найти

Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:

1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.

2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.

3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2

4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.

5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.

6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь

8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.

9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.

10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.

11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0

12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.

13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.

14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.

Источник