По каким траекториям движутся как луне

Видимое движение и фазы Луны

Сидерический и синодический месяц — Движение Луны на небесной сфере — Смена лунных фаз

Сидерический и синодический месяцы

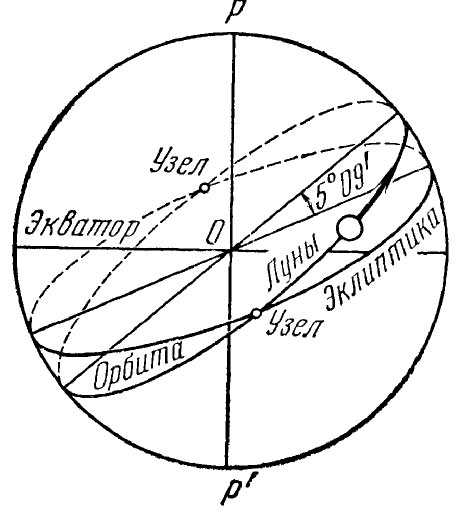
Луна является естественным спутником Земли и ближайшим к ней небесным те­лом. Она обращается вокруг Зе­мли по эллиптической орбите в том же направлении, что и Зем­ля вокруг Солнца. Среднее расстояние Луны от Земли равно 384 400 км. Плоскость орбиты Луны наклонена к плоскости эк­липтики на 5°09′.

Наклон орбиты Луны к плоскости эклиптики

Точки пересечения орбиты Луны с эклиптикой называются узлами лунной орбиты. Движение Лупы вокруг Земли для наблюдателя представляется как ви­димое ее движение по небесной сфере. Видимый путь Луны по небесной сфере называется видимой орбитой Луны.

За сутки Луна перемещается по видимой орбите относительно звезд примерно на 13,2°, а относительно Солнца на 12,2°, так как Солнце за это время тоже перемещается по эклиптике в среднем на 1°. Промежуток времени, в течение которого Луна со­вершает полный оборот по своей орбите относительно звезд, назы­вается звездным, или сидерическим месяцем. Его продолжительность равна 27,32 средних солнечных суток.

Промежуток времени, в течение которого Луна совершает пол­ный оборот по своей орбите относительно Солнца, называется синодическим месяцем. Он равен 29,53 средних солнечных су­ток.

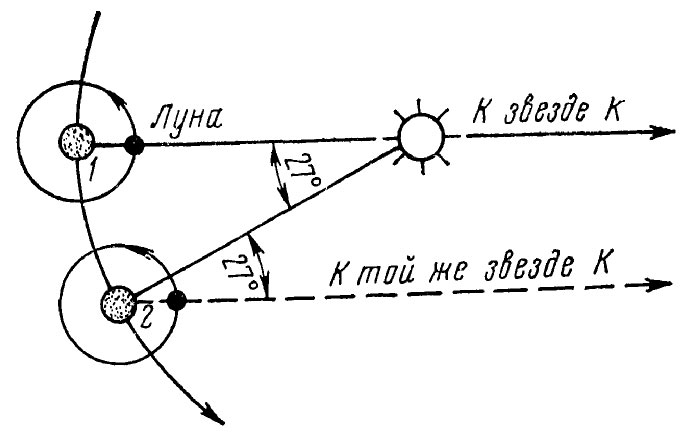
Сидерический и синодический месяцы различаются примерно на двое суток за счет движения Земли по своей орбите вокруг Солнца. На рисунке ниже показано, что при нахождении Земли на ор­бите в точке 1 Луна и Солнце наблюдаются на небесной сфере в одном и том же месте, например на фоне звезды К.

Синодический и сидерический месяцы

Через 27,32 сут, т. е. когда Лупа сделает полный оборот вокруг Земли, она снова будет наблюдаться на фоне той же звезды. Но так как Земля вме­сте с Луной за это время переместится по своей орбите относитель­но Солнца примерно на 27° и будет находиться в точке 2, то Луне необходимо еще пройти 27°, чтобы занять прежнее положение от­носительно Земли и Солнца, на что понадобится около 2 сут. Та­ким образом, синодический месяц длиннее сидерического на отре­зок времени, который нужен Луне, чтобы переместиться на 27°.

Движение Луны на небесной сфере

Период вращения Луны вокруг своей оси равен периоду ее об­ращения вокруг Земли. Поэтому Луна обращена к Земле всегда одной и той же стороной. Вследствие того, что Луна за одни сутки перемещается по небесной сфере с запада на восток, т. е. в сторо­ну, обратную суточному движению небесной сферы, на 13,2°, ее восход и заход ежесуточно запаздывают примерно на 50 мин.

Это ежедневное запаздывание приводит к тому, что Луна непрерывно меняет свое положение относительно Солнца, но через строго опре­деленный период времени вновь возвращается в исходное положе­ние. В результате движения Луны по видимой орбите происходит непрерывное и быстрое изменение ее экваториальных координат.

В среднем за сутки прямое восхождение Луны изменя­ется на 13,2°, а склонение — на 4°. Изменение экваториальных координат Луны происходит не только за счет ее быстрого дви­жения по орбите вокруг Земли, но и вследствие необычайной сложности этого движения. На Луну действуют многие силы, име­ющие различную величину и период, под влиянием которых все эле­менты лунной орбиты постоянно изменяются.

Наклон орбиты Луны к эклиптике колеблется в пределах от 4°59′ до 5°19′ за время, несколько меньшее полугода. Изменяются формы и размеры орбиты. Непрерывно с периодом 18,6 года меняется положение орбиты в пространстве, в результате чего происхо­дит перемещение узлов лунной орбиты навстречу движению Луны.
Это приводит к постоянному изменению угла наклона видимой ор­биты Луны к небесному экватору от 28°35′ до 18°17′. Поэтому пределы изменения склонения Луны не остаются постоянными. В некоторые периоды оно изменяется в пределах ±28°35′, а в дру­гие — ±18° 17′.

Смена лунных фаз во время движения на небесной сфере

Движение Луны на небесной сфере сопровождается непрерывным изменением ее внешнего вида. Происходит так называемая смена лунных фаз. Фазой Луны называется видимая часть лунной поверхности, освещенная солнечными лучами.

Рассмотрим, вследствие чего происходит изменение лунных фаз. Известно, что Луна светит отраженным солнечным светом- Половина ее поверхности всегда освещена Солнцем. Но вследствие различных взаимных положений Солнца, Луны и Земли освещен­ная поверхность представляется земному наблюдателю в разных видах. Принято разли­чать четыре фазы Луны: новолу­ние, первая четверть, пол­нолуние и последняя чет­верть.

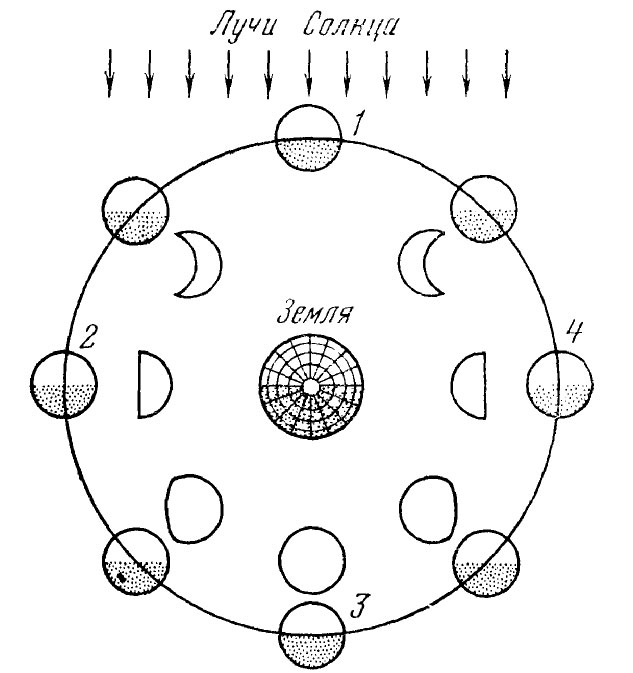
Положения и фазы
Луны (1 – новолуние, 2 – первая четверть, 3 – полнолуние, 4 – последняя четверть)

Во время новолуния Луна про­ходит между Солнцем и Землей. В этой фазе Луна обращена к Зем­ле неосвещенной стороной, и поэто­му она не видна земному наблюда­телю.

В фазе первой четверти Луна находится в таком положении, что наблюдатель видит ее в виде поло­вины освещенного диска.

Во время полнолуния Луна находится в на­правлении, противоположном на­правлению на Солнце. Поэтому к Земле обращена вся освещенная сторона Луны и она видна в виде полного диска. После полнолуния видимая с Земли освещенная часть Луны постепенно уменьшается.

Когда Луна достигает фазы последней четверти, она снова видна в виде половины освещенного диска. В Северном полушарии в пер­вой четверти освещена правая половина диска Луны, а в послед­ней — левая.

В промежутке между новолунием и первой четвертью и в про­межутке между последней четвертью и новолунием к Земле обра­щена небольшая часть освещенной Луны, которая наблюдается в виде серпа. В промежутках между первой четвертью и полнолу­нием, полнолунием и последней четвертью Луна видна в виде ущербленного диска.

Полный цикл смены лунных фаз происходит в течение строго определенного периода времени. Его называют периодом фаз. Он равен синодическому месяцу, т. е. 29,53 сут.

Промежуток времени между основными фазами Луны равен примерно 7 сут. Количество дней, прошедших с момента новолу­ния, принято называть возрастом Луны. С изменением возраста изменяются и точки восхода и захода Луны.

Движение Луны вокруг Земли является причиной лунных и солнечных затмений – затмения происходят только тогда, когда Солнце и Луна одновременно располагаются вблизи узлов лунной орбиты. Солнечное затмение происходит, когда Луна находится ме­жду Солнцем и Землей, т. е. в период новолуния, а лунное — когда Земля находится между Солнцем и Луной, т. е. в период полно­луния.

Источник

По каким траекториям движутся как луне

§ 14. Д вижение небесных тел под действием сил тяготения

1. Закон всемирного тяготения

С огласно закону всемирного тяготения, изученному в курсе физики,

все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

F = G ,

где m 1 и m 2 — массы тел; r — расстояние между ними; G — гравитационная постоянная.

Открытию закона всемирного тяготения во многом способствовали законы движения планет, сформулированные Кеплером, и другие достижения астрономии XVII в. Так, знание расстояния до Луны позволило Исааку Ньютону (1643—1727) доказать тождественность силы, удерживающей Луну при её движении вокруг Земли, и силы, вызывающей падение тел на Землю.

Ведь если сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна, находящаяся от Земли на расстоянии примерно 60 её радиусов, должна испытывать ускорение в 3600 раз меньшее, чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с 2 . Следовательно, ускорение Луны должно составлять 0,0027 м/с 2 .

В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение

где ω — угловая скорость Луны; r — радиус её орбиты. Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять r = 60 • 6 400 000 м = 3,84 • 10 8 м. Звёздный период обращения Луны T = 27,32 суток, в секундах составляет 2,36 • 10 6 с. Тогда ускорение орбитального движения Луны

a = • r = • 3,84 • 10 8 м = 0,0027 м/с 2 .

Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.

Можно убедиться и в том, что при движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения. Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит d и квадратов периодов обращения T есть величина постоянная:

= = = . = const.

Ускорение планеты равно

a = = = 4 π 2 .

Из третьего закона Кеплера следует

= ,

поэтому ускорение планеты равно

a = 4 π 2 • const .

Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения.

2. Возмущения в движении тел Солнечной системы

З аконы Кеплера строго выполняются, если рассматривается движение двух изолированных тел (Солнце и планета) под действием их взаимного притяжения. Однако в Солнечной системе планет много, все они взаимодействуют не только с Солнцем, но и между собой. Поэтому движение планет и других тел не в точности подчиняется законам Кеплера. Отклонения тел от движения по эллипсам называются возмущениями .

Возмущения эти невелики, так как масса Солнца гораздо больше массы не только отдельной планеты, но и всех планет в целом. Наибольшие возмущения в движении тел Солнечной системы вызывает Юпитер, масса которого в 300 раз превышает массу Земли. Особенно заметны отклонения астероидов и комет при их прохождении вблизи Юпитера.

В настоящее время возмущения учитываются при вычислении положения планет, их спутников и других тел Солнечной системы, а также траекторий космических аппаратов, запускаемых для их исследования. Но ещё в XIX в. расчёт возмущений позволил сделать одно из самых известных в науке открытий «на кончике пера» — открытие планеты Нептун.

Проводя очередной обзор неба в поиске неизвестных объектов, Вильям Гершель в 1781 г. открыл планету, названную впоследствии Ураном. Спустя примерно полвека стало очевидно, что наблюдаемое движение Урана не согласуется с расчётным даже при учёте возмущений со стороны всех известных планет. На основе предположения о наличии ещё одной «заурановой» планеты были сделаны вычисления её орбиты и положения на небе. Независимо друг от друга эту задачу решили Джон Адамс в Англии и Урбен Леверье во Франции. На основе расчётов Леверье немецкий астроном Иоганн Галле 23 сентября 1846 г. обнаружил в созвездии Водолея неизвестную ранее планету — Нептун. Это открытие стало триумфом гелиоцентрической системы, важнейшим подтверждением справедливости закона всемирного тяготения. В дальнейшем в движении Урана и Нептуна были замечены возмущения, которые стали основанием для предположения о существовании в Солнечной системе ещё одной планеты. В 1930 г. после просмотра большого количества фотографий звёздного неба был обнаружен Плутон, который, как оказалось, является одним из множества объектов, расположенных за орбитой Нептуна.

3. Масса и плотность Земли

З акон всемирного тяготения позволил определить массу нашей планеты. Исходя из закона всемирного тяготения, ускорение свободного падения можно выразить так:

g = G .

Подставим в формулу известные значения этих величин: g = 9,8 м/с 2 , G = 6,67 • 10 –11 Н • м 2 /кг 2 , R = 6370 км — и получим, что масса Земли M = 6 • 10 24 кг.

Зная массу и объём земного шара, можно вычислить его среднюю плотность: 5,5 • 10 3 кг/м 3 . С глубиной за счёт увеличения давления и содержания тяжелых элементов плотность возрастает.

4. Определение массы небесных тел

Б олее точная формула третьего закона Кеплера, которая была получена Ньютоном, даёт возможность определить одну из важнейших характеристик любого небесного тела — массу. Выведем эту формулу, считая (в первом приближении) орбиты планет круговыми.

Пусть два тела, имеющие массы m 1 и m 2 , взаимно притягивающиеся и обращающиеся вокруг общего центра масс, находятся от центра масс на расстоянии r 1 и r 2 и обращаются вокруг него с периодом T . Расстояние между их центрами R = r 1 + r 2 . На основании закона всемирного тяготения ускорение каждого из этих тел равно:

a 1 = G , a 2 = G .

Угловая скорость обращения вокруг центра масс составляет ω = . Тогда центростремительное ускорение выразится для каждого тела так:

a 1 = r 1 , a 2 = r 2 .

Приравняв полученные для ускорений выражения, выразив из них r 1 и r 2 и сложив их почленно, получаем:

G = = ( r 1 + r 2 ),

= .

Поскольку в правой части этого выражения находятся только постоянные величины, оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, — Солнце и планета, планета и спутник. Определим массу Солнца, для этого запишем выражение:

= ,

где M — масса Солнца; m 1 — масса Земли; m 2 — масса Луны; T 1 и a 1 — период обращения Земли вокруг Солнца (год) и большая полуось её орбиты; T 2 и a 2 — период обращения Луны вокруг Земли и большая полуось лунной орбиты.

Пренебрегая массой Земли, которая ничтожно мала по сравнению с массой Солнца, и массой Луны, которая в 81 раз меньше массы Земли, получим:

= .

Подставив в формулу соответствующие значения и приняв массу Земли за единицу, мы получим, что Солнце примерно в 333 тыс. раз по массе больше нашей планеты.

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях. Об определении массы звёзд см. в § 23.

П од действием взаимного притяжения частиц тело стремится принять форму шара. Если эти тела вращаются, то они деформируются, сжимаются у полюсов.

Кроме того, изменение их формы происходит и под действием взаимного притяжения, которое вызывают явления, называемые приливами . Давно известные на Земле, они получили объяснение только на основе закона всемирного тяготения.

Рис. 3.13. Схема лунных приливов

Рассмотрим ускорения, создаваемые притяжением Луны в различных точках земного шара (рис. 3.13). Поскольку точки A , B и O находятся на различных расстояниях от Луны, ускорения, создаваемые её притяжением, будут различны.

Разность ускорений, вызываемых притяжением другого тела в данной точке и в центре планеты, называется приливным ускорением.

Приливные ускорения в точках A и B направлены от центра Земли. В результате Земля, и в первую очередь её водная оболочка, вытягивается в обе стороны по линии, соединяющей центры Земли и Луны. В точках A и B наблюдается прилив, а вдоль круга, плоскость которого перпендикулярна этой линии, на Земле происходит отлив. Тяготение Солнца также вызывает приливы, но из-за большей его удалённости они меньше, чем вызванные Луной. Приливы наблюдаются не только в гидросфере, но и в атмосфере и в литосфере Земли и других планет.

Вследствие суточного вращения Земля стремится увлечь за собой приливные горбы, в то же время вследствие тяготения Луны, которая обращается вокруг Земли за месяц, полоса приливов должна перемещаться по земной поверхности значительно медленнее. В результате между огромными массами воды, участвующей в приливных явлениях, и дном океана возникает приливное трение. Оно тормозит вращение Земли и вызывает увеличение продолжительности суток, которые в прошлом были значительно короче (5—6 ч). Тот же эффект ускоряет орбитальное движение Луны и приводит к её медленному удалению от Земли. При этом приливы со стороны Земли на Луне затормозили её вращение, и она теперь обращена к Земле одной стороной. Такое же медленное вращение характерно для многих спутников Юпитера и других планет. Сильные приливы, вызываемые на Меркурии и Венере Солнцем, по-видимому, являются причиной их крайне медленного вращения вокруг оси.

6. Движение искусственных спутников Земли и космических аппаратов к планетам

В озможность создания искусственного спутника Земли теоретически обосновал ещё Ньютон. Он показал, что существует такая горизонтально направленная скорость , при которой тело, падая на Землю, тем не менее на неё не упадёт, а будет двигаться вокруг Земли, оставаясь от неё на одном и том же расстоянии. При такой скорости тело будет приближаться к Земле вследствие её притяжения как раз на столько, на сколько из-за кривизны поверхности нашей планеты оно будет от неё удаляться (рис. 3.14). Эта скорость, которую называют первой космической (или круговой), известна вам из курса физики:

v 1 = = 7,9 • 10 3 м/с = 7,9 км/с.

Рис. 3.14. Орбита искусственного спутника Земли

Практически осуществить запуск искусственного спутника Земли оказалось возможно лишь через два с половиной столетия после открытия Ньютона — 4 октября 1957 г. За время, прошедшее с этого дня, который нередко называют началом космической эры человечества, искусственные спутники самого различного устройства и назначения заняли важное место в нашей повседневной жизни. Они обеспечивают непрерывный мониторинг погоды и других природных явлений, трансляции телевидения и т. п. Спутниковая навигационная система ГЛОНАСС и другие системы глобального позиционирования позволяют в любой момент с высокой степенью точности определить координаты любой точки на Земле. Пожалуй, нет в наши дни ни одной глобальной проблемы, в решении которой не принимали участие искусственные спутники Земли (ИСЗ).

Космические аппараты (КА), которые направляются к Луне и планетам, испытывают притяжение со стороны Солнца и согласно законам Кеплера так же, как и сами планеты, движутся по эллипсам. Скорость движения Земли по орбите составляет около 30 км/с. Если геометрическая сумма скорости космического аппарата, которую ему сообщили при запуске, и скорости Земли будет больше этой величины, то КА будет двигаться по орбите, лежащей за пределами земной орбиты. Если меньше — то внутри орбиты Земли. В первом случае, если аппарат летит к Марсу (рис. 3.15) или другой внешней планете, энергетические затраты будут наименьшими, если КА достигнет орбиты этой планеты при своём максимальном удалении от Солнца — в афелии. Кроме того, необходимо так рассчитать время старта КА, чтобы к этому моменту в ту же точку своей орбиты пришла планета. Иначе говоря, начальная скорость и день запуска КА должны быть выбраны таким образом, чтобы КА и планета, двигаясь каждый по своей орбите, одновременно подошли к точке встречи. Во втором случае — для внутренней планеты — встреча с КА должна произойти в перигелии его орбиты (рис. 3.16). Такие траектории полётов называются полуэллиптическими . Большие оси этих эллипсов проходят через Солнце, которое находится в одном из фокусов, как и полагается по первому закону Кеплера.

Рис. 3.15. Траектория полёта KA к Марсу

Рис. 3.16. Траектория полёта KA к Венере

Конструкция и оборудование современных КА обеспечивают возможность совершения ими весьма сложных манёвров — выход на орбиту спутника планеты, посадка на планету, передвижение по её поверхности и т. п.

В опросы 1. Почему движение планет происходит не в точности по законам Кеплера? 2. Как было установлено местоположение планеты Нептун? 3. Какая из планет вызывает наибольшие возмущения в движении других тел Солнечной системы и почему? 4. Какие тела Солнечной системы испытывают наибольшие возмущения и почему? 5. По каким траекториям движутся космические аппараты к Луне; к планетам? 6*. Объясните причину и периодичность приливов и отливов. 7*. Будут ли одинаковы периоды обращения искусственных спутников Земли и Луны, если эти спутники находятся на одинаковых расстояниях от них?

У пражнение 12 1. Определите массу Юпитера, зная, что его спутник, который отстоит от Юпитера на 422 000 км, имеет период обращения 1,77 суток. Для сравнения используйте данные для системы Земля—Луна. 2. Ускорение силы тяжести на Марсе составляет 3,7 м/с 2 , на Юпитере — 25 м/с 2 . Рассчитайте первую космическую скорость для этих планет. 3. Сколько суток (примерно) продолжается полёт КА до Марса, если он проходит по эллипсу, большая полуось которого равна 1,25 а. е.?

Источник