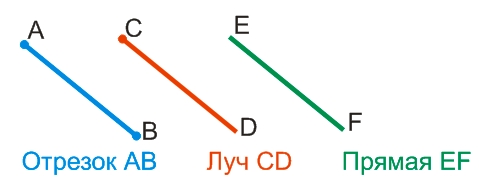
Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)
— это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
точка 1, точка 2, точка 3
— это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
Линия может быть
- , если её начало и конец находятся в одной точке,
- , если её начало и конец не соединены
замкнутые линии
разомкнутые линии
самопересекающиеся линии
линии без самопересечений
прямые линии
ломанные линии
кривые линии
— это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
прямая линия AB
Прямые могут быть
- , если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- , если пересекаются под прямым углом (90°).
- , если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
— это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
луч AB
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
— это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
прямая линия AB
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
— это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
(похожи на звенья цепи) — это отрезки, из которых состоит ломанная. — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
— это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
— это замкнутая ломанная линия
(помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. — это смежные звенья ломанной.
— это вершины ломанной. — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
Источник
Что такое луч в математике
Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.
Луч — геометрическое понятие
Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.
На картинке вы можете посмотреть, что такое луч и как он выглядит:
Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.
Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.
Отличия луча от прямой и от отрезка
В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.
В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.
В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.
Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:
- отрезок имеет начальную и конечную точки;
- луч — только начало;
- прямая — не располагает начальной и конечной точками.
Взаимное расположение лучей
Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.
На рисунке начало для лучей — общая точка A.
По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.
Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.
Дополнительные лучи — это фигуры, которые обладают такими признаками, как:
- имеют совпадающее начало в одной точке;
- располагаются на одной прямой линии;
- направляются в разные стороны, то есть угол между ними составляет 180 градусов.
Можно ли сравнить два луча?
Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.
Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.
Луч — альтернативные значения слова
Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.
Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.
Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:
В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.
Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.
Источник
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
- Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
- Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
- Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
- Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
1) а – это прямая.
2) АВ – это отрезок.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.
Источник
Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Любая фигура, будь она объемной, плоскостной или линейной, состоит из множества точек — таких себе математических аналогов атомов реального мира.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
- прямая не имеет ни начала, ни конца;
- луч имеет начало, но не имеет конца;
- отрезок имеет начало и конец.
Важно понимать, что математическая прямая, луч или отрезок не имеют такого понятия, как толщина — это прямые линии, состоящие из совокупности точек, стоящих «плечом к плечу» рядом друг с другом. Математическая точка не имеет никакой размерности — она может характеризоваться только координатами.
Провести «настоящую» прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
- отрезок с обеих сторон ограничивается точками;
- у луча точка ставится в его начале;
- прямая точками не ограничивается.
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
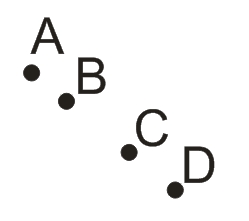
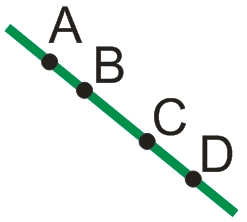
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
Проведем одну прямую через точки A и D, а вторую прямую — через точки В и С.
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Частный случай скрещивающихся прямых — перпендикулярные прямые.
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Чтобы сделать вывод являются ли скрещивающися прямые перпендикулярными, достаточно знать величину одного из четырех углов, которые образуют скрещивающиеся прямые — если любой из таких углов равен 90°, то и все три остальных будут также равны 90°, т. е., прямые будут перпендикулярными. Если же какой-либо из углов не равен 90°, то ни один из углов не будет равен 90°, а, значит, такие прямые не будут перпендикулярными.
Доказать это очень просто.
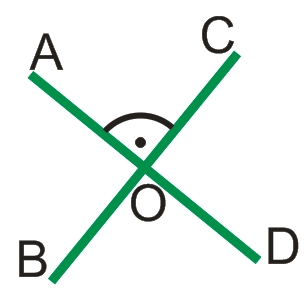
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Источник