Отражение света от луны это рассеянное отражение рассеяние света или нет

Поляризация: рассеяние и отражение

Физика > Поляризация рассеянием и отражением

Рассмотрите угол поляризации света в момент отражения или рассеяния. Читайте, что такое угол Брюстера при падении света и чему равен, преломление лучей света.

Неполяризованный свет можно поляризовать искусственно и природными явлениями, вроде отражения и рассеяния.

Задача обучения

Определить угол отражения полной поляризации, основываясь на показателях преломления.

Основные пункты

Если неполяризованный объект оказывается на отражающей поверхности, то вертикально поляризованные аспекты преломляются.
При отражении образовывается угол, когда свет полностью поляризован. Его именуют углом Брюстера.
Неполяризованный свет может поляризоваться, если рассеивается в воздухе.

Термины

Показатель преломления – соотношение скорости света в вакууме и ином материале.
Поляризация – создание поляризованного света.

Поляризация отражением

Отраженный свет способен слегка поляризоваться из-за отражения. Многие световые источники формируют неполяризованный свет. Когда он оказывается на отражающей плоскости, то вертикальные поляризованные аспекты преломляются. Отраженный более горизонтально также поляризуется. Чтобы разобраться, воспринимайте свет, как стрелу, а отражающая поверхность станет мишенью. Если стрела оказалась в цели перпендикулярно (вертикально поляризована), то прилипнет (преломляется). Если попадет в цель со своей стороны (горизонтально), то отобьется.

Неполяризованный свет обладает равным количеством вертикальной и горизонтальной поляризации. При контакте с поверхностью вертикальные составляющие впитываются или преломляются, оставляя отраженный свет немного поляризованным

Так как свет делится на два пучка, а одна часть преломляется, то величина поляризации отраженного основывается на показателе преломления поверхности. Для вычисления используем формулу:

(θ_b – угол отражения полной поляризации, n₁ – показатель преломления среды, в которой будет проходить отраженный свет; n₂ – показатель преломления среды, отражающей свет).

Поляризация рассеянием

Неполяризованный свет способен поляризоваться рассеянием. Световые волны выступают электромагнитными, поэтому будут приводить в вибрацию электроны воздушных молекул, расположенных перпендикулярно направленности перемещения. Далее электроны выпускают лучи, поляризующие также перпендикулярно. Свет выступает параллельным исходящему лучу и полностью поляризуется.

Неполяризованное рассеяние встряхивает электроны воздуха перпендикулярно направленности исходящего луча. Поэтому рассеянный свет обладает перпендикулярной поляризацией по отношению к изначальной направленности

Источник

Законы отражения света

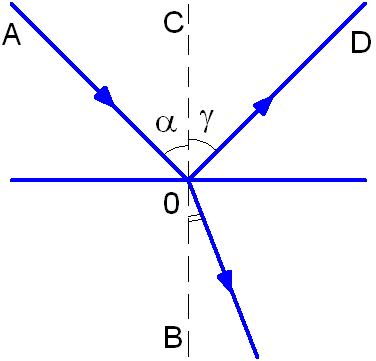
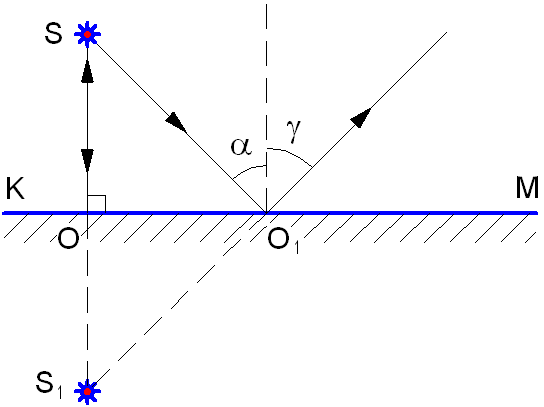
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

Рис. 1.3. Отражение и преломление света.

Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

1	Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости.
2	Угол отражения γ равен углу падения α :

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

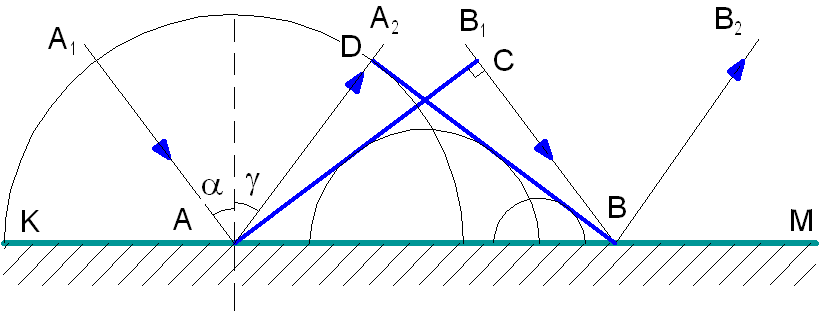
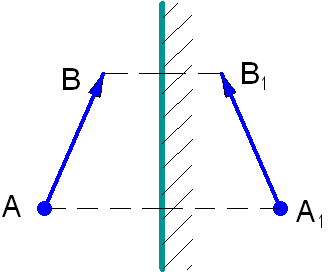
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

Рис. 1.4. Построение Гюйгенса.

А₁А и В₁В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА₂ и ВВ₂.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ .

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

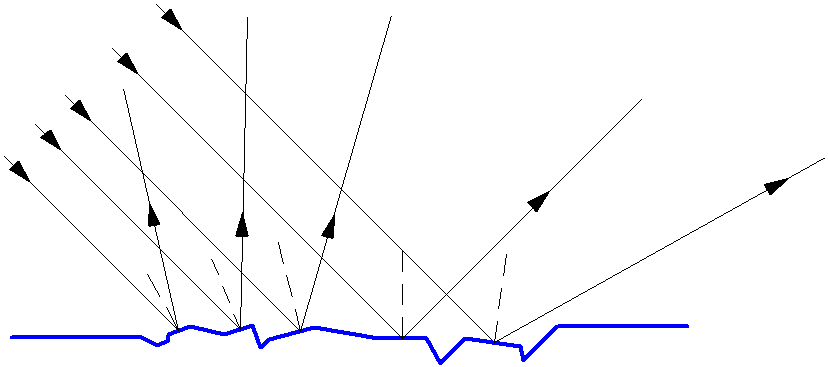
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

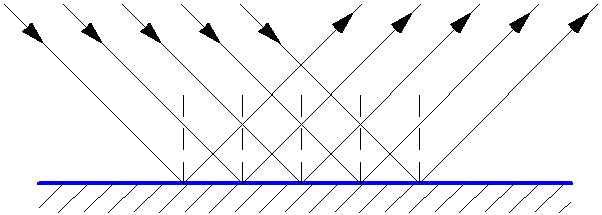
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO₁.

Луч SO₁ падает на зеркало под углом α и отражается под углом γ ( α = γ ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S₁, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S₁, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S₁расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

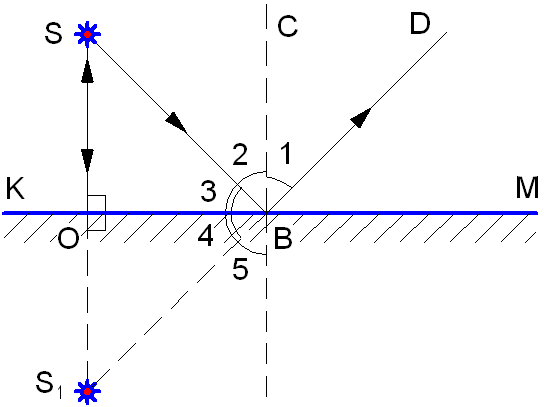
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS₁OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS₁, то есть точка S₁ расположена симметрично точке S относительно зеркала.

Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Источник

Почему свет от луны отражается не логично?

Рассеянное отражение. Сторона Луны, которая напротив Солнца, должна быть самой яркой. Во время полнолуний Солнце и Земля находятся от Луны с одной стороны. Казалось бы, во время полнолуний Луна должна выглядеть как матовый шар, освещенный со стороны Солнца/Земли, а не как диск.

Но лунная поверхность отражает свет неравномерно, наверное, поэтому мы и видим «диск» (плюс еще какая-нибудь адаптация зрения в темноте влияет на эффект):

А теперь то, что сказал Картофельный папа, только простым языком :))

То отражение света, которое ты описал, работает для зеркал: заркало гладенькое и, действительно, отражает свет прямо, по закону «угол падения равен углу отражения». Только вот поверхность Луны не ровная, там камни, пыль, т. е. по всей Луне куча микроскопических неровностей. ОТ КАЖДОЙ такой неровности свет будет отражаться по закону «угол падения равен углу отражения», вот и получим отраженный свет во все стороны.

На рисуночке золотистые стрелки обозначают падающий свет, красные — отраженный, жирная чёрная линия — неровная отражающая поверхность.

Анализ наблюдательных данных показал, что лунная поверхность обладает следующими фотометрическими свойствами:

1) для образований с одинаковым альбедо яркость в полнолуние одинакова в любой точке диска;
2) все области без исключения имеют максимальную яркость в полнолуние;
3) если исключить различие в альбедо, изофоты для любой фазы приблизительно следуют по меридианам (таким образом, фотометрическая функция почти не зависит от фотометрической широты);
4) все образования с одинаковой долготой характеризуются сходными значениями фотометрической функции, хотя различия, связанные с местными условиями, все же существуют;
5) яркость всех областей до (или после) полнолуния увеличивается (или уменьшается) быстрее, чем по линейному закону, такое поведение кривых характеризует свойство лунного закона отражения, называемое обратным рассеянием;
6) скорость увеличения яркости особенно велика при малых фазовых углах, этот факт известен как оппозиционный эффект.
Дальнейшие экспериментальные исследования позволили уточнить эти свойства лунной поверхности. В частности, было обнаружено, что яркость поверхности Луны всё же зависит от фотометрической широты, причём на больших углах фазы эта зависимость становится весьма существенной.
Альбедо Луны всего 7%, поэтому возможен такой эффект из-за того, что плохо освещенные объекты для нас теряют рельеф. Плюс постоянное шевеление лунной пыли от неравномерного нагрева и солнечного ветра. Но есть еще утверждение, что на поверхности Луны ВСЕ фотографии получаются черно-белыми. А это уже другая физика.

Источник