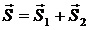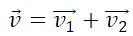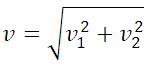Видимое годовое движение солнца на небесной сфере
Истинное движение Земли — Видимое годовое движение Солнца на небесной сфере — Небесный экватор и плоскость эклиптики — Экваториальные координаты Солнца в течение года
Истинное движение Земли
Чтобы понять принцип видимого движения Солнца и других светил на небесной сфере, рассмотрим сперва истинное движение Земли. Земля является одной из планет солнечной системы. Она непрерывно вращается вокруг своей оси.
Период вращения ее равен одним суткам, поэтому наблюдателю, находящемуся на Земле, кажется, что все небесные светила обращаются вокруг Земли с востока на запад с тем же периодом.
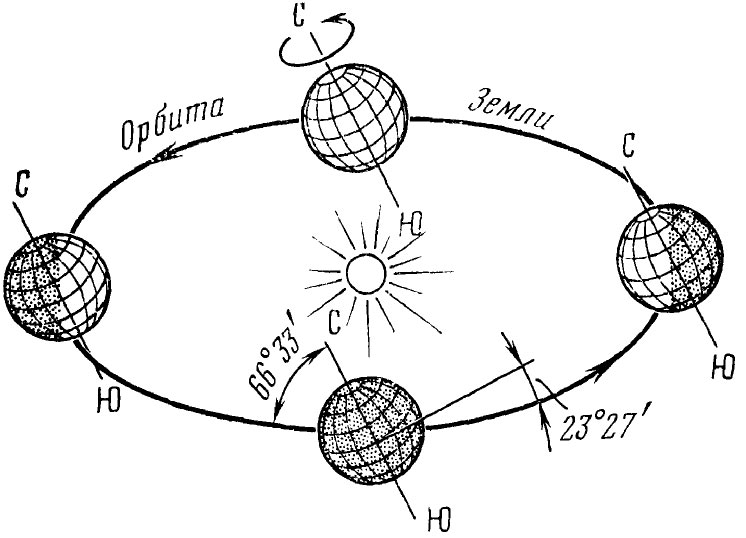
Наклон оси вращения Земли к плоскости орбиты
Но Земля не только вращается вокруг своей оси, но и обращается также вокруг Солнца по эллиптической орбите. Полный оборот вокруг Солнца она совершает за один год. Ось вращения Земли наклонена к плоскости орбиты под углом 66°33′. Положение оси в пространстве при движении Земли вокруг Солнца все время остается почти неизменным. Поэтому Северное и Южное полушария попеременно бывают обращены в сторону Солнца, в результате чего на Земле происходит смена времен года.
При наблюдении неба можно заметить, что звезды на протяжении многих лет неизменно сохраняют свое взаимное расположение.
Звезды “неподвижны” лишь потому, что находятся очень далеко от нас. Расстояние до них так велико, что с любой точки земной орбиты они видны одинаково.
А вот тела же солнечной системы — Солнце, Луна и планеты, которые находятся сравнительно недалеко от Земли, и смену их положений мы можем легко заметить. Таким образом, Солнце наравне со всеми светилами участвует в суточном движении и одновременно имеет собственное видимое движение (оно называется годовым движением), обусловленное движением Земли вокруг Солнца.
Представьте себе картину — Луна взяла и исчезла с орбиты Земли. Чем нам может грозить такой поворот событий? Подробнее об этом
Видимое годовое движение Солнца на небесной сфере
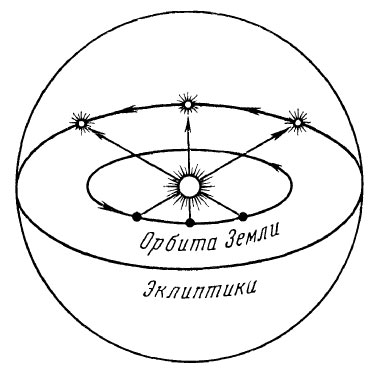
Наиболее просто годовое движение Солнца можно объяснить по рисунку приведенному ниже. Из этого рисунка видно, что в зависимости от положения Земли на орбите наблюдатель с Земли будет видеть Солнце на фоне разных созвездий. Ему будет казаться, что оно все время перемещается по небесной сфере. Это движение является отражением обращения Земли вокруг Солнца. За год Солнце сделает полный оборот.
Что представляет собой эклиптика
Большой круг на небесной сфере, по которому происходит видимое годовое движение Солнца, называется эклиптикой. Эклиптика — слово греческое и в переводе означает затмение. Этот круг назвали так потому, что затмения Солнца и Луны происходят только тогда, когда оба светила находятся на этом круге.
Следует отметить, что плоскость эклиптики совпадает с плоскостью орбиты Земли.
Видимое годовое движение Солнца по эклиптике происходит в том же направлении, в котором Земля движется по орбите вокруг Солнца, т. е. оно перемещается к востоку. В течение года Солнце последовательно проходит по эклиптике 12 созвездий, которые образуют пояс Зодиака и называются зодиакальными.
Пояс Зодиака образуют следующие созвездия: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог и Водолей. Вследствие того, что плоскость земного экватора наклонена к плоскости орбиты Земли на 23°27 ‘ , плоскость небесного экватора также наклонена к плоскости эклиптики на угол е=23°27′.
Наклон эклиптики к экватору не сохраняется постоянным (вследствие воздействия на Землю сил притяжения Солнца и Луны), поэтому в 1896 г. при утверждении астрономических постоянных решено было наклон эклиптики к экватору считать усредненно равным 23°27’8″,26.
Небесный экватор и плоскость эклиптики
Эклиптика пересекается с небесным экватором в двух точках, которые называются точками весеннего и осеннего равноденствий. Точку весеннего равноденствия принято обозначать знаком созвездия Овен Т, а точку осеннего равноденствия — знаком созвездия Весов —. Солнце в этих точках соответственно бывает 21 марта и 23 сентября. В эти дни на Земле день равен ночи, Солнце точно восходит в точке востока и заходит в точке запада.
Точки весеннего и осеннего равноденствия – места пересечения экватора и плоскости эклиптики
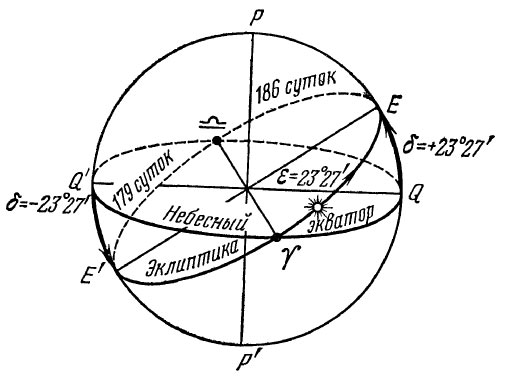
Точки эклиптики, отстоящие от точек равноденствий на 90°, называются точками солнцестояний. Точка Е на эклиптике, в которой Солнце занимает самое высокое положение относительно небесного экватора, называется точкой летнего солнцестояния, а точка Е’, в которой оно занимает самое низкое положение, называется точкой зимнего солнцестояния.
В точке летнего солнцестояния Солнце бывает 22 июня, а в точке зимнего солнцестояния — 22 декабря. В течение нескольких дней, близких к датам солнцестояний, полуденная высота Солнца остается почти неизменной, в связи с чем эти точки и получили такое название. Когда Солнце находится в точке летнего солнцестояния день в Северном полушарии самый длинный, а ночь самая короткая, а когда оно находится в точке зимнего солнцестояния — наоборот.
В день летнего солнцестояния точки восхода и захода Солнца максимально удалены к северу от точек востока и запада на горизонте, а в день зимнего солнцестояния они имеют наибольшее удаление к югу.
Движение Солнца по эклиптике приводит к непрерывному изменению его экваториальных координат, ежедневному изменению полуденной высоты и перемещению по горизонту точек восхода и захода.
Известно, что склонение Солнца отсчитывается от плоскости небесного экватора, а прямое восхождение — от точки весеннего равноденствия. Поэтому когда Солнце находится в точке весеннего равноденствия, его склонение и прямое восхождение равны нулю. В течение года склонение Солнца в настоящий период изменяется от +23°26′ до —23°26′, переходя два раза в год через нуль, а прямое восхождение от 0 до 360°.
Солнце имеет форму шара или сплюснуто у полюсов? Давайте разберемся! Подробнее об этом
Экваториальные координаты Солнца в течение года
Экваториальные координаты Солнца в течение года изменяются неравномерно. Происходит это вследствие неравномерности движения Солнца по эклиптике и движения Солнца по эклиптике и наклона эклиптики к экватору. Половину своего видимого годового пути Солнце проходит за 186 суток с 21 марта по 23 сентября, а вторую половину за 179 суток с 23 сентября по 21 марта.
Неравномерность движения Солнца по эклиптике связана с тем, что Земля на протяжении всего периода обращения вокруг Солнца движется по орбите не с одинаковой скоростью. Солнце находится в одном из фокусов эллиптической орбиты Земли.
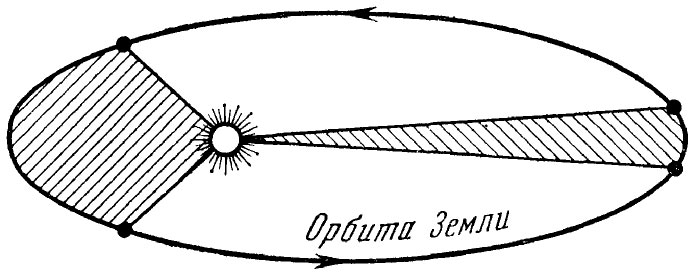
движение Земли по орбите
Из второго закона Кеплера известно, что линия, соединяющая Солнце и планету, за равные промежутки времени описывает равные площади. Согласно этому закону Земля, находясь ближе всего к Солнцу, т. е. в перигелии, движется быстрее, а находясь дальше всего от Солнца, т. е. в афелии — медленнее.
Ближе к Солнцу Земля бывает зимой, а летом — дальше. Поэтому в зимние дни она движется по орбите быстрее, чем в летние. Вследствие этого суточное изменение прямого восхождения Солнца в день зимнего солнцестояния равно 1°07′, тогда как в день летнего солнцестояния оно равно только 1°02′.
Различие скоростей движения Земли в каждой точке орбиты вызывает неравномерность изменения не только прямого восхождения, но и склонения Солнца. Однако за счет наклона эклиптики к экватору его изменение имеет другой характер. Наиболее быстро склонение Солнца изменяется вблизи точек равноденствия, а у точек солнцестояния оно почти не изменяется.
Знание характера изменения экваториальных координат Солнца позволяет производить приближенный расчет прямого восхождения и склонения Солнца.
Для выполнения такого расчета берут ближайшую дату с известными экваториальными координатами Солнца. Затем учитывают, что прямое восхождение Солнца за сутки изменяется в среднем на 1°, а склонение Солнца в течение месяца до и после прохождения точек равноденствия изменяется на 0,4° в сутки; в течение месяца перед солнцестояниями и после них — на 0,1° в сутки, а в течение промежуточных месяцев между указанными — на 0,3°.
Источник
95. Приведите примеры равномерного движения.
Встречается очень редко, например, движение Земли вокруг Солнца.
96. Приведите примеры неравномерного движения.
Движение автомобиля, самолета.
97. Мальчик скатывается на салазках с горы. Можно ли это движение считать равномерным?
Нет.
98. Сидя в вагоне движущегося пассажирского поезда и наблюдая движение встречного товарного поезда, нам кажется, что товарный поезд идет гораздо быстрее, чем шел до встречи наш пассажирский поезд. Почему это происходит?
Относительного пассажирского поезда, товарный движется с суммарной скоростью пассажирского и товарного поездов.
99. В движении или покое находится водитель движущегося автомобиля относительно:
а) дороги;
б) сидения автомобиля;
в) автозаправки;
г) Солнца;
д) деревьев вдоль дороги?
В движении: а, в, г, д
В покое: б
100. Сидя в вагоне движущегося поезда, мы наблюдаем в окне автомобиль, который уходит вперед, затем кажется неподвижным, и, наконец, движется назад. Как объяснить то, что мы видим?
Вначале скорость автомобиля выше скорости поезда. Затем скорость автомобиля становится равной скорости поезда. После этого, скорость автомобиля уменьшается, по сравнению со скоростью поезда.
101. Самолет выполняет «мертвую петлю». Какую траекторию движения видят наблюдатели с земли?
Кольцевую траекторию.
102. Приведите примеры движения тел по криволинейным траекториям относительно земли.
Движение планет вокруг Солнца; движение катера по реке; полет птицы.
103. Приведите примеры движения тел, имеющих прямолинейную траекторию относительно земли.
Движущийся поезд; идущий прямо человек.
104. Какие виды движения мы наблюдаем при письме шариковой ручкой? Мелом?
Равномерное и неравномерное.
105. Какие части велосипеда при его прямолинейном движении описывают относительно земли прямолинейные траектории, а какие – криволинейные?
Прямолинейное: руль, седло, рама.
Криволинейное: педали, колеса.
106. Почему говорят, что Солнце всходит и заходит? Что в данном случае является телом отсчета?
Телом отсчета рассматривается Земля.
107. Два автомобиля движутся по шоссе так, что некоторое расстояние между ними не меняется. Указать, относительно каких тел каждый из них находится в покое и относительно каких тел они в течение этого промежутка времени движутся.
Относительно друг друга автомобили находятся в покое. Относительно окружающих предметов автомобили движутся.
108. Санки скатываются с горы; шарик скатывается по наклонному желобу; камень, выпущенный из рук, падает. Какие из этих тел движутся поступательно?
Поступательно движутся санки с горы и камень, выпущенный из рук.
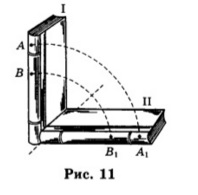
109. Книга, установленная на столе в вертикальном положении (рис. 11, положение I), от толчка падает и занимает положение II. Две точки А и В на переплете книги при этом описали траектории АА1 и ВВ1. Можно ли сказать, что книга двигалась поступательно? Почему?
Нет, так траектория АА1 не равна траектории ВВ1.
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля

Урок 02. (дополнительный материал). Относительность механического движения
Относительность механического движения.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным.
Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляетсяотносительность механического движения.
Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен. Например, пассажир в покоящемся поезде смотрит на проходящий мимо поезд и не понимает, какой поезд движется, пока не посмотрит на небо или землю.
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Движение одного и того же тела может выглядеть по-разному с точки зрения различных наблюдателей. Скорость, направление движения и вид траектории тела будут различными для различных наблюдателей. Без указания тела отсчета разговор о движении является бессмысленным. Например, сидящий пассажир в поезде покоится относительно вагона, но движется вместе с вагоном относительно платформы вокзала.
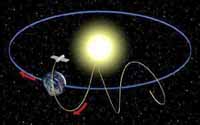
Проиллюстрируем теперь для различных наблюдателей различие вида траектории движущегося тела. Находясь на Земле, на ночном небе легко можно видеть яркие быстро летящие точки — спутники. Они движутся по круговым орбитам вокруг Земли, то есть вокруг нас. Сядем теперь в космический корабль, летящий к Солнцу. Мы увидим, что теперь каждый спутник движется не по окружности вокруг Земли, а по спирали вокруг Солнца:
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).
Системы, которые вращаются или ускоряются, неинерциальные.
Землю нельзя считать вполне ИСО: она вращается, но для большинства наших целей системы отсчета, связанные с Землей, в достаточно хорошем приближении можно принять за инерциальные. Система отсчета, движущаяся равномерно и прямолинейно относительно ИСО, также инерциальная.
Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.
Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений.
Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую.
В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле.
Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя.
Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ.
В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ.
Следовательно, положение тел и их скорости в разных системах отсчета различны.
Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.
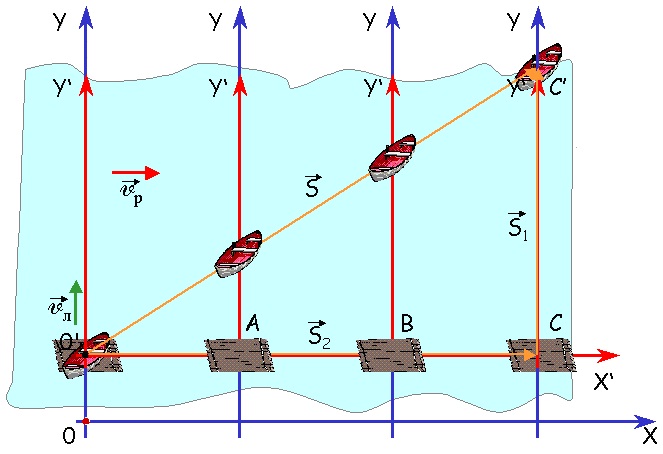
Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.
С каждым наблюдателем свяжем систему координат.
X0Y – неподвижная система координат.
X’0’Y’ – подвижная система координат.
S – перемещение лодки относительно неподвижной СО.
S1 – перемещение лодки относительно подвижной СО
S2 – перемещение подвижной системы отсчета относительно неподвижной СО.
По закону сложения векторов
Скорость получим разделив S на t:
v – скорость тела относительно неподвижной СО
v1 – скорость тела относительно подвижной СО
v2 – скорость подвижной системы отсчета относительно неподвижной СО
Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.
В скалярном виде формула будет иметь вид:
Впервые эту формулу получил Галилей.
Принцип относительности Галилея: все инерциальные системы отсчета равноправны; ход времени, масса, ускорение и сила в них записываются одинаково.
Скачать презентацию с Яндекса
Источник