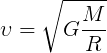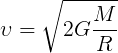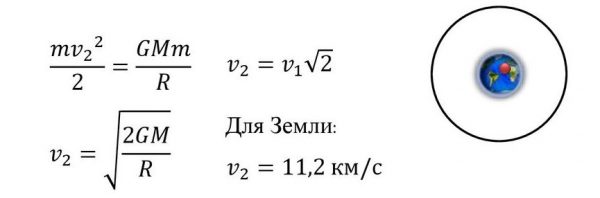Формулы радиуса, орбитальной скорости и периода пл
Формулы для расчета радиуса, скорости орбитального движения и периода планет.
При расчетах используются величины:
— радиус орбиты R (при условном круговом движении) в а.е.
— период T (земной год)
— орбитальная скорость V а.е./год
1. Соотношение радиуса и скорости.
Произведение радиуса и квадрата скорости для всех планет одинаково.
R V2 = const
(получается от преобразований третьего закона Кеплера: R3/ T2 const)
R V2 = R V2 — для разных радиусов обрит разных планет и разных радиусов кривизны одной планеты.
производим вычисления:
для Земли — 1 х 6.28 х 6.28 / 1 = 39.434
где V — 2х 3.14 х R / T 2 х 3.14 х 1 : 1 = 6.28 а.е. /год
для Марса 1.532 х 5.07 х 5.07 = 39.379
скорость для марса : 2 х 3.14 х 1.52 : 1.88 = 5, 07 а.е. / год
радиус орбиты Марса взят средний — он колеблется от 1.405 (перигелий) до 1.693 (афелий)
для Юпитера 5.2 х 2.75 х 2.75 = 39.325
скорость 2 х 3.14 х 5.2 : 11.86 = 2.75 а.е. / год
2. Соотношение радиуса и периода.
Для вычисления периода по радиусу орбиты можно использовать следующую формулу:
Радиус, умноженный на корень квадратный из радиуса, дает период.
(Если единица измерения радиуса — а.е.
то период получается в земных годах.)
получается, что для каждой планеты есть некое число, которое умноженное на себя дает радиус орбиты, а умноженное на себя еще раз — дает период.
Для Марса это число примерно 1.232, для Юпитера 2.28, для Урана 4.38,
для Плутона 6.26 , для Венеры 0.85
Получается числовой ряд планет:
Меркурий 0.62 0.387 0.24
Венера 0.85 0.723 0.615
Земля 1 1 1
Марс 1.232 1.52 1.88
Юпитер 2.28 5.2 11.86
Сатурн 3.09 9.58 29.6
Уран 4.38 19.18 84.048
где: первое это некое базовое число; второе радиус; третье период.
зависимость:1 — число, 2- число возведенное в квадрат, 3- возведенное в куб.
Базовое число планеты — соотношение скоростей Земли и планеты.
А соотношение скоростей Земли и планеты получается из соотношения квадратных корней радиусов этих планет.
Теперь, если взять, например, орбитальную скорость Земли за единицу,
то орбитальная скорость Земли относительно скорости Марса 1.2328.
тогда: радиус обриты Марса есть 1.2328 х 1.2328 = 1.52 а.е.
а период орбиты Марса 1.52 = 1.2328 = 1.8739 в земных годах
что в упрощенной записи :
Vз : V м (Vз :V м ) 2 = R (Vз :V м ) 2 х R = T
или n , далее n в квадрате и n в кубе.
где n Vз :V м — отношение скоростей Земли и Марса.
R V2 = const (получается от преобразований третьего закона Кеплера)
4. Квадрат движения.
Для понимания сути движения планет интересно сделать ещё и такое построение.
Все планеты СС одновременно движутся по своим орбитам. Если взять некий общий отрезок времени,то каждая из планет пройдет за это время по орбите своё раcстояние.
Если на основе этого расстояния, построить квадрат, то площадь этого квадрата для каждой планеты будет пропорциональна орбитальной скорости.
И, если площадь этого квадрата умножить на радиус орбиты, то для всех планет получится одинаковое число, выражающее объём.
И получиться некая константа трехмерного пространства.
Это можно выразить так:
Квадрат расстояния пройденной каждой планетой за общую единицу времени обратно пропорционален радиусам их орбит или произведение радиуса обриты на квадрат расстояния для всех планет за общую единицу времени есть величина одинаковая.
5. Период соединения.
Есть ещё одна формула которая позволяет вычислить через какое время произойдет соединение планет планеты.
Т1 х Т2 / Т2-Т1
6. И, конечно, каждая планета за одну единицу времени проходит угол (сектор), который по отношению к земному, обратно пропорционален периодам.
Формулы могут применяться и для расчета параметров движения спутников.
На рисунке: Таблица соотношения параметров планет Солнечной системы относительно Земли.
комментарии к таблице.
Данные для других планет выражен по отношению к параметрам дв. Земли.
Соотношение скоростей мы понимаем, как соотношение путей пройденных планетой по своей орбите за единицу времени. Соотношение скоростей, возведенное в квадрат дает соотношение радиусов, а возведенное в куб — соотношение периодов планет.
Источник
Формулы и калькулятор космических скоростей
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.
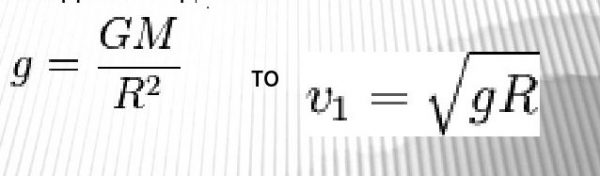
Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Источник
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
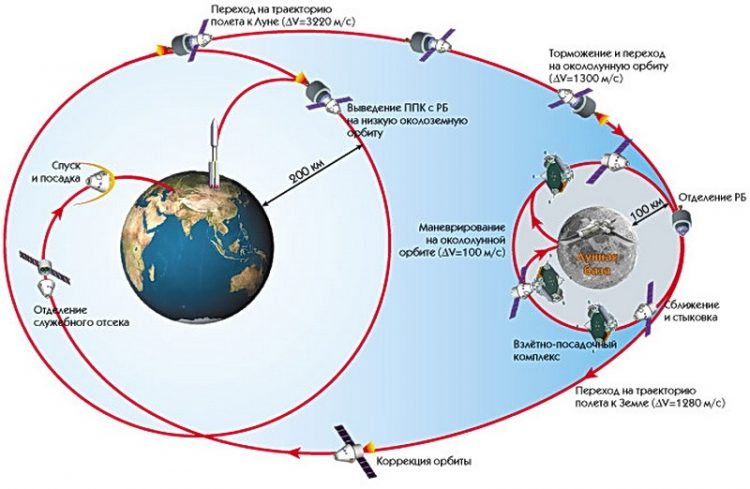
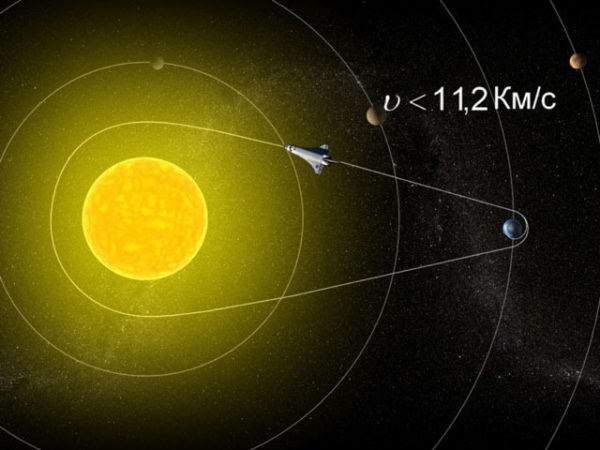
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
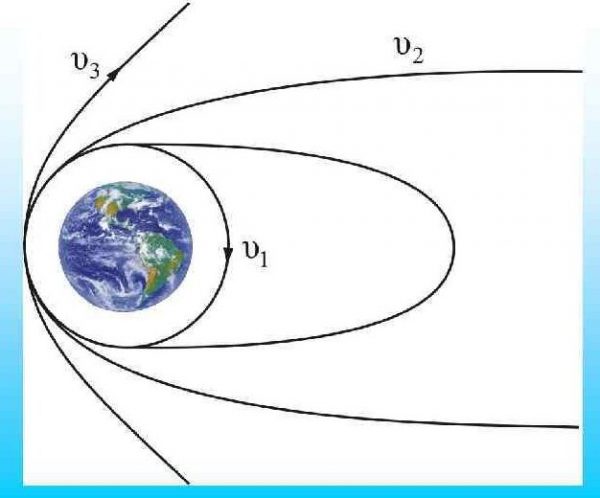
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник