Орбита Солнца
Согласно подсчетам исследователей, Солнцу понадобится 226 млн. лет для того, чтобы сделать полный оборот вокруг нашей галактики, или центра Млечного Пути (Инф. из интернета).
Но есть ещё одна орбита у Солнца вокруг обьекта Х со скоростью приблизительно 20 км/сек. Об этом говорится реже.
Предполагаю, что есть у Солнца и ещё одна орбита, внутри Солнечной Системы. Диаметр её от одного центра эллипса орбиты Земли, до другого центра. (В одном из которых находится Солнце. Кеплер 1 закон). Это значит, что Солнце не стоит на месте, а двигаясь в рукаве Галактики, имеет движение внутри собственной системы.
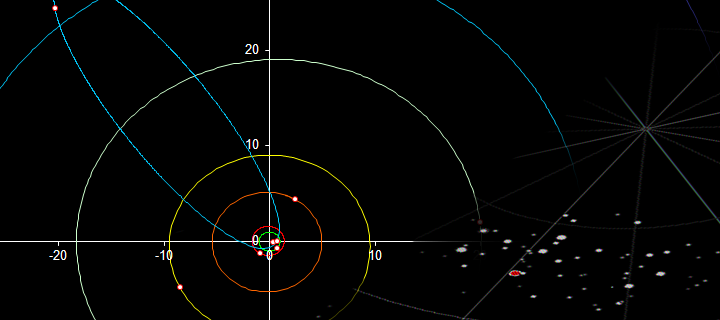
Вот как это выглядит:
Рассмотрим, как образовывается эллипс от круга. Допустим, что расстояние от центра круга, до центра одного из двух центров эллипса равно 6 млн. км. Следует диаметр между центрами равен 12 млн. км. , а длина окружности (Пи*Д). То есть, 12 умножаем на 3,14 равно 37, 68 млн. км. .
Теперь предположим, что это орбита Солнца вокруг Чёрной дыры (центра окружности).
Так, как Солнце, имеет несколько ускорений при движении.
1. Движение к Полярной звезде. 220-240 км/сек.
2. Движение к обьекту Х — 20 км/сек.
3. Движение вокруг Белой дыры рядом с собой — Приблизительно, за 1 один час 14 000 километров. (Мои вычисления). Белая дыра*, — поступление материи в Солнечную систему.
Белая дыра* — Обратная сторона Чёрной дыры.
4. Разумно предположить, что появление пятен на Солнце, есть ни что иное, как работа Белой дыры. А мы, Земляне, видим прохождение пятен около Солнца. Тем более, что это соответствует действительности, так как, температура пятен намного ниже, чем температура самой поверхности Солнца.
5. Пятна исчезают при закрытых порталах центра (Белой дыры). Может цикл и есть 11 лет?
6. Само Солнце двигаясь вперёд проходит с определённой периодичностью две точки центров орбиты, скажем, планеты Земля. Поэтому, Солнце всегда является центром масс.
7. Белая дыра Солнечной системы, работает на приём материи из другого пространства, а из этого следует, что выход спирали материи происходит с выбросом наружу. (На Марсе жизнь была, на Земле есть, на Венере будет)!
8. В нашей Галактике «Млечный Путь» четыре рукава. Посмотрите как они расположены. (Рисунок из интр. вверху). Солнечная система и планета Земля находится в рукаве Ориона. Чёрная дыра Солнечной системы это нулевой потенциал между рукавами Галактики. Через который и проходит материя.
28. 01. 2018 год Из Одинцово.
Виктор Кармалитов.
Источник
Орбита Солнца
Может показаться на первый взгляд, что все вокруг чего-то передвигается. Луна крутится вокруг нашей планеты, а Земля обходит по Солнечной орбите. Однако, известно ли вам, что Солнце имеет орбиту вокруг такой галактики, как Млечный Путь?
Графическое представление орбиты Солнца
Ученные рассчитали, что Солнцу потребуется 226 миллионов лет, чтобы полностью обойти орбиту вокруг центра Млечного Пути. Иными словами, Солнце пребывало в пространстве около Млечного Пути, когда динозавры управляли на Земле. Фактически Солнце совершило 20,4 оборотов по своей орбите с того периода времени, как оно сформировалось 4,6 млрд лет назад.
Так как Солнце находится на расстоянии около 26,000 световых лет от сердца Млечного пути, оно должно путешествовать по круговой орбите вокруг центра Млечного пути на удивительной скорости — 782,000 км/час. Просто для сравнения, Земля вращается со скоростью 1,770 км/ч, а ее перемещение по орбите вокруг Солнца со скоростью 108,000 км/час.
Считается, что Солнце продолжит плавить водород еще на протяжении 7 миллиардов лет или что-то приблизительно около того. Другими словами, Солнце имеет еще только оставшиеся 31 орбиту, которые сделают это до того, как исчерпается топливо. Конечно, мы не можем наблюдать движение Солнца по орбите в телескопы. Однако на нашем сайте есть 3D-модели онлайн для галактики, где показано не только осевое движение Солнца, но и облет вокруг галактического центра.
Источник
Орбита Солнца
Луна, являясь спутником нашей планеты, вращается вокруг неё, в то время как сама Земля совершает обороты вокруг Солнца. Наряду с этим звезда движется вокруг галактической группы под названием Млечный Путь (далее по тексту – МП). Какова орбита Солнца, будет рассмотрено в данной статье.
Перемещение звезды по галактике
Опытные астрономы провели расчёты и поняли, что один оборот вокруг центральной части галактики происходит за 226 млн лет. Говоря на более простом языке, в последний раз, когда Солнце пребывало в своём нынешнем положении, здесь главенствовали динозавры.
Согласно официальной истории, за весь период своего существования наше светило успело сделать 20,4 оборотов вокруг Млечного пути, если принимать во внимание тот факт, что его образование произошло 4,6 млрд лет тому назад. Так как орбита Солнца проходит достаточно далеко от МП, движение звезды происходит на достаточно высокой скорости, равное 914 400 километра в час. Земля, в свою очередь, перемещается с параметром в 108 000 км/ч.
Направление, в котором движется Солнце, в официальной астрономической науке называется Апексом. В настоящее время оно направляется к созвездию Геркулес. Есть распространённая версия, указывающая на то, что наша звезда будет светить ещё на протяжении 7 млрд лет, то есть успеет совершить ещё 31 оборот.
Дополнительная информация
Орбита Солнца проходит через МП, который представляет собой галактическую группу спирального типа, имеющую диаметральное сечение, равное порядка 30 600 парсек (альтернативное измерение – 100 000 лет – световых). В составе её около 300 млрд звёзд.
Располагается данная система неподалёку от плоскости симметрии, к которой относится галактический диск. А точнее – немного севернее по отношению к нему, на дистанции около 8300 парсек от центра галактики, на самой окраине рукава Ориона. Обращение звезды происходит непосредственно вокруг центра галактики по круговой орбите. Скоростной режим при этом составляет 254 километра в секунду, данное значение было уточнено в 2009 году. Галактический год равен 230 млн лет.
Теперь понятно, вокруг чего вращается Солнце. Наряду с движением кругового типа система колеблется также в вертикальном направлении. Поэтому она оказывается, как в северном, так и в южном галактическом полушарии. Её местоположение оказывает существенное влияние на эволюцию земной жизни. Орбита является практически круглой, и скорость имеет то же значение, что и скорость спиральных рукавов. Это значит, что межзвёздная стабильность представлена долгими периодами времени, что для Земли однозначно хорошо.
Наряду с этим солнечная система располагается достаточно далеко от окрестностей, которые переполнены звёздами. Для галактического центра характерно внушительное излучение, которое могло оказать влияние на развитие жизни высочайших организмов. Некоторые учёные считают, что через 2 млрд лет произойдёт столкновение между МП и Большим Магеллановым облаком.
Таким образом, стало ясно, вокруг чего вращается Солнце, и как это происходит.
Источник
Как астрономы измерили расстояние от Земли до Солнца?
Как астрономы вычислили расстояние от Солнца до нашей планеты, размер Солнца, или скорость движения Земли по орбите вокруг него? Очевидно, что ответ на один из этих вопросов объяснит и другие. Но как можно найти ответ на первый?
В первую очередь, чтобы вычислить расстояние Земля-Солнце (обозначим A ) необходимо найти относительные расстояния между Землёй и другими планетами.
Рассмотрим орбиту Венеры. В первом приближении орбиты Венеры
и Земли представляют собой идеальные круги вокруг Солнца, причём находящиеся в одной плоскости.
Взгляните на рисунок ниже:
По схеме становится ясно, что есть две точки, в которых угол Солнце-Венера-Земля составляет 90° . В этих точках угловое расстояние между Венерой и Солнцем достигает максимально возможного значения,
при наблюдениях с Земли.
Если посмотреть на движение Венеры относительно Солнца, то можно заметить, что она сначала отдаляется до определённого предела, а затем снова начинает двигаться к Солнцу.
Зная угол Солнце-Земля-Венера (обозначим e ) по тригонометрическим формулам несложно определить расстояния:
Земля-Венера = A x cos ( e )
Венера-Солнце = A x sin ( e )
Максимальное угловое расстояние Солнце-Венера 46° . Отсюда расстояние Солнце-Венера составляет 72% расстояния Солнце-Земля.
Попытки вычислить расстояние Земля-Солнце предпринимались с древних времён
Первым из известных людей, применивших геометрию для оценки расстояния Земля-Солнце был древнегреческий астроном Аристарх Самосский (310-230 гг. до н.э.). Принцип его рассуждений был верен , однако измерения оказались ошибочны .
Ещё один древнегреческий учёный Эратосфен (276-194 гг. до н.э.) выражал вычисленное значение в древних единицах измерения — стадиях . Однако из-за разногласий в пересчётах стадия в метры невозможно наверняка утверждать о верности полученных им результатов.
Первое точное и научно обоснованное измерение расстояния Земля-Солнце выполнил итальянский астроном Кассини в 1672 по движению Марса. 100 лет спустя серия наблюдений за Венерой дала ещё более точное значении.
С 1961 года расстояние до Венеры можно определить непосредственно, применяя радиолокацию
Серия радиоволн передаётся с Земли, отражается от поверхности Венеры и возвращается обратно. По времени прохождения волн измеряется расстояние. Известно, что радиоволны распространяются со скоростью света.
Как упомянуто вначале, зная расстояние Земля-Солнце можно рассчитать остальные параметры.
Солнце, как можно наблюдать с нашей планеты, имеет угловой радиус около 0,5°. Диаметр Солнца можно вычислить через A:
2 x Rsun = tan (0,5°) x A
Зная время, затраченное Землёй на один оборот вокруг Солнца (P = 1 год) и расстояние пройденное за этот период ( 2πA , орбита Земли практически круговая) можно рассчитать среднюю орбитальную скорость:
Источник
Расчет положения небесных тел на небосводе. Часть 1
Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.
В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.
Всех любопытных прошу под кат.
Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.
Так как же движутся планеты?
В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.
Кеплерова орбита
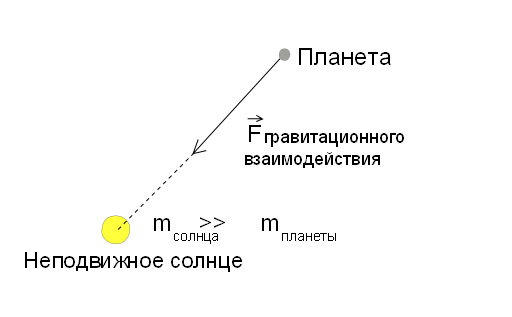
Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так: 
Гравитационное взаимодействие
Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: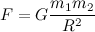 
Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу сферическую планету в вакууме материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.
Второй закон Ньютона
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость: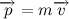 
Таким образом, запишем словесную формулировку в символьном виде: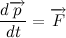 
Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу: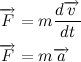 
Где вектор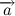 
— ускорении тела. Не забываем, что ускорение, импульс, скорость и сила величины векторные. Давайте условимся, что если над векторной величиной стоит знак вектора, то понимается именно вектор, в противном случае его модуль.
Второй закон Кеплера
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).
Дифференциальное уравнение орбиты
Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором: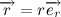 
Тогда вектор скорости будет равен: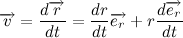 
А векторное произведение радиус вектора на скорость в свою очередь: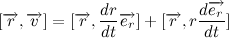 
Учитывая тот факт, что вектора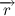 
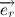
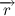
и 
совпадают по направлению, а следовательно совпадают по направлению и вектора и 
, получаем, что 
. Тогда: 
Давайте разберем, что такое производная единичного вектора по времени: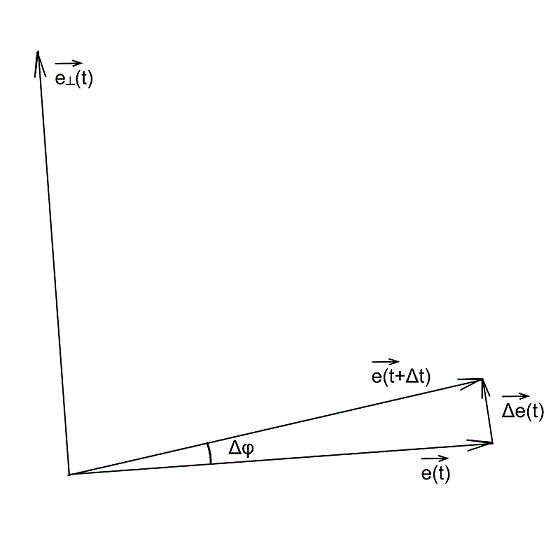 
Из рисунка видно, что за время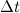 
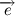
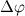
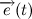
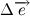
вектор 
поворачивается на угол 
. Разность векторов 
и 
равна вектору 
. Для малых углов справедливо следующее соотношение: 
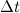
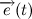
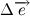
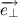
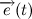
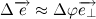
В пределе, когда устремляется к нулю, направления векторов и совпадают, а направление вектора перпендикулярно к ним. Введем единичный вектор 
, перпендикулярный к и совпадающий с направлением движения его конца, тогда: 
Таким образом, переходя к пределу, получим: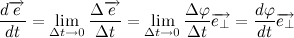 
Где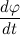 
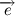
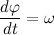
это угловая скорость вектора . Обозначим 
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что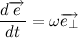 
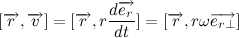
получим: 
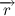
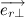
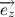
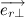
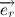
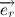
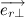
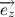
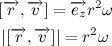
Несложно заметить, что вектора и 
взаимно перпендикулярны. Введем еще один единичный вектор 
, который перпендикулярен к векторам и . Таким образом, вектора , и образуют ортонормированный базис. Исходя из определения векторного произведения, получим: 
Следовательно,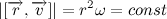 
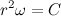
. Введем обозначение, 
. Так же стоит отметить, что: 
Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт :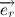 
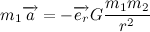
Где m1 и m2 — масса планеты и солнца соответственно.
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, 
, тогда: 
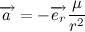
Теперь давайте распишем вектор ускорения: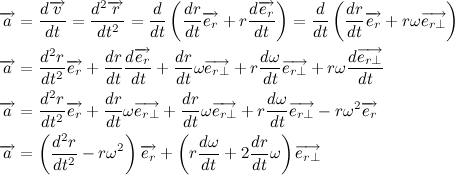 
Рассмотрим содержимое второй скобки: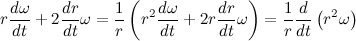 
Но мы уже знаем, что 
, отсюда следует, что 
, тогда: 
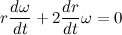
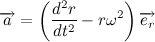
Введем обозначение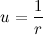 
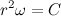
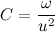
. Напомню, что раннее мы ввели обозначение , очевидно, что 
.
Теперь распишем производную от модуля радиус вектора через С: 
Теперь распишем вторую производную от модуля радиус вектора через С: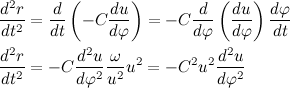 
Учитывая полученный результат, перепишем выражение для вектора ускорения: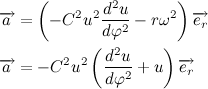 
Тогда второй закон Ньютона примет вид: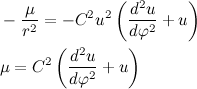 
Перепишем полученное дифференциальное уравнение в более привычный вид: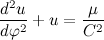 
Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.
Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.
Что нам еще предстоит
В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.
Источник