ОБ ОПТИМАЛЬНЫХ ТРАЕКТОРИЯХ ПОЛЕТА КА К ЛУНЕ В СИСТЕМЕ ЗЕМЛЯ-ЛУНА-СОЛНЦЕ
(ON OPTIMAL TRAJECTORIES OF SPACE FLIGHT TO THE MOON IN THE EARTH-MOON-SUN SYSTEM
Preprint, Inst. Appl. Math., the Russian Academy of Science)
Ивашкин В.В.
(V.V.Ivashkin)
ИПМ им. М.В.Келдыша РАН
Москва, 2001
Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты №№ 01-01-00133, 00-15-96036)
Аннотация
Исследуются траектории нового типа для космического полета от Земли к Луне. В отличие от обычных траекторий прямого полета к Луне исследуемые траектории предполагают сначала полет за орбиту Луны и за границу сферы действия Земли, на расстояние около 1,5 млн.км от Земли и только затем – полет к Луне. При этом подлет к Луне происходит не по гиперболической, а по эллиптической неустойчивой селеноцентрической орбите, т.е. осуществляется временный захват космического аппарата (КА) Луной. Это приводит к существенной экономии энергетики при торможении движения КА вблизи Луны для перехода на конечную устойчивую орбиту спутника Луны или для посадки на ее поверхность. Дается качественный анализ возмущения Солнцем для увеличения перигейного расстояния орбиты КА и возмущения Землей для гашения селеноцентрической энергии движения КА. Приведены характеристики траекторий полета от Земли к Луне, полученных с помощью численного интегрирования уравнений движения КА в системе Земля-Луна-Солнце.
Ключевые слова: полет к Луне, оптимальные траектории, торможение у Луны, гравитационные возмущения, захват Луной.
Abstract
New trajectories for space flight from the Earth to the Moon founded recently are studied in the paper. These trajectories, unlike usual ones of direct flight to the Moon, use at first a flight beyond the Moon and the Earth sphere of influence, at a distance of about 1.5 m km from the Earth and only then a flight to the Moon. In this case a celenocentric flight near the Moon takes place not along a hyperbolic orbit but along an unstable elliptic one, that is a temporary capture by the Moon. This results in essential economy of a fuel outlay when braking the spacecraft (SC) motion near the Moon for transfer to a final stable orbit of the Moon’s satellite or for a soft landing on its surface. A qualitative analysis of the Sun’s perturbations for increasing a perigee distance of the SC orbit as well the Earth’s perturbations for decreasing a celenocentric energy of the SC motion is given. Characteristics of a trajectories of the space flight from the Earth to the Moon received by a numerical integration of the SC motion equations in the Earth-Moon-Sun system are presented.
Key words: flight to Moon, optimal trajectories, braking near Moon, gravity perturbations, capture by Moon.
Проф. Егорову Всеволоду Александровичу и Prof. Martinez Garcia Juan Jose посвящается
2. Траектории «прямого» полета ка от земли к луне
3. БИЭЛЛИПТИЧЕСКИЕ траектории полета ка к луне
в системе земля-луна
3.1. п ереходы между орбитами в центральном гравитационном поле
3.2. Б иэллиптический полет к Луне в модельной системе Земля-Луна
4. АНАЛИЗ «ОБХОДНОГО» ПОЛЕТА КА К ЛУНЕ В СИСТЕМЕ
4.1. Схема и основные особенности «обходного» полета
4.2. Оценка влияния гравитации Солнца на перигейное
расстояние орбиты КА
4.3. Оценка влияния гравитации Земли на гашение энергии
селеноцентрического движения КА
4.4. Оценка влияния гравитации Земли при эволюции на
конечную эллиптическую орбиту у Луны
5. ЧИСЛЕННЫЕ ХАРАКТЕРИСТИКИ ТРАЕКТОРИЙ «ОБХОДНОГО»
5.1. Модель расчета траектории
5.2. Характеристики «обходного» полета к Луне
2. TRAJECTORIES OF DIRECT SPACE FLIGHT FROM THE EARTH
3. TRAJECTORIES OF BIELLIPTICAL SPACE FLIGHT TO THE MOON
IN THE EARTH-MOON SYSTEM
3.1. O rbital transfers in central gravitational field
3.2. Bielliptical space flight to the Moon in model Earth-Moon system
4. ANALYSIS OF “BYPASS” SPACE FLIGHT TO THE MOON IN THE
4.1. S cheme and principal peculiarities of “bypass” flight
4.2. Evaluation of the Sun gravity influence on a spacecraft orbit perigee
4.3. Evaluation of the Earth gravity influence on a spacecraft celenocentric energy extinguishing
4.4. Evaluation of the Earth gravity influence for evolution to final
celenocentric elliptical orbit
5. NUMERICAL CHARACTERISTICS OF TRAJECTORY OF “BYPASS” FLIGHT TO THE MOON
5.1. m odel of a trajectory calculation
5.2. Some characteristics of “bypass” flight to the Moon
1. Введение
В работе делается анализ траекторий полета к Луне нового типа, для которых характерны большие (> 1 млн. км) расстояния отлета от Земли, большое (
100 сут.) время полета, но и уменьшенные энергетические затраты на торможение у Луны за счет эллиптичности орбиты подлета к Луне. Сначала, в п. 2, дан анализ обычных траекторий «прямого» полета к Луне. Затем, в п. 3, исследованы характеристики биэллиптических траекторий полета к Луне в модельной системе Земля-Луна. Нa основе этого в п. 4 описана схема и выделены особенности построения «обходных» траекторий в реальной системе Земля — Луна — Солнце, даны оценки гравитационных возмущений для этих траекторий, доказывающие реализуемость временного захвата КА Луной. В п. 5 приведена модель численного расчета и представлены основные численные характеристики некоторых полученных траекторий, на которых осущест-вляется захват КА Луной и уменьшается энергетика торможения при переходе на орбиту спутника или при посадке на ее поверхность.
2. Траектории “прямого” полета КА от Земли к Луне
Исследование характеристик космического полета от Земли к Луне важно как для космонавтики, так и для небесной механики. Это явилось стимулом появления множества работ, посвященных данной проблеме. Особенно важными, как с практической, так и с теоретической точек зрения, оказались работы В.А. Егорова [1 – 4 и др.], в которых выполнен очень полный анализ траекторий полета от Земли к Луне.
Важными являются также результаты В.А. Егорова по захвату точки Луной, ибо даже в случае временного захвата точки оказывается возможным пассивное, без затрат топлива создание спутника Луны, а в случае торможения затраты топлива будут меньше, чем при гиперболическом подлете к Луне. Анализ В.Г. Фесенкова [5] и В.А. Егорова [1 –4] показал, что вопрос о полном захвате Луной точки является достаточно сложным и до конца нерешенным. Для случая движения в рамках круговой ограниченной задачи трех тел оказался невозможным захват Луной КА, запущенного с Земли на первом витке его траектории. Для произвольных траекторий была доказана теорема о невозможности захвата точки лишь для случая достаточно малого отношения масс главных тел ( -4 ). Однако В.А. Егоров (1957г.) отметил, что возможен временный захват точки Луной и дал идею построения траекторий временного захвата, проходящих вблизи точки либрации L 1 . Это было затем подтверждено результатами ряда исследований, см., например, M . C . Davidson [6], B .Себехей [7], E . Belbruno [8]. Правда, эти траектории захвата проходили далеко от Земли.
В связи с выполненным В.А. Егоровым и в большинстве других работ анализом траекторий КА от Земли к Луне следует отметить два обстоятельства. В.А. Егоров [1] сделал оценку возмущения Солнцем D FS движения точки в сфере действия Земли, при r FE , D FS / FE D FS / FE пределы, то недалеко.
Выполненный В.А. Егоровым анализ траекторий полета от Земли к Луне в рамках указанной модели – системы Земля – Луна – имел фундаментальный характер и послужил основой определения практически всех траекторий полета от Земли к Луне. Эти траектории имеют ряд общих черт и иногда сейчас называют траекториями “прямого” полета. Для примера на рис. 1 приведена схематично траектория полета к Луне советского КА «Луна-9», запущенного 31.01.1966 г. и осуществившего 3.02.1966 г. первую мягкую посадку на Луну [9].
Для этой траектории время полета на Луну составляет
3.5 сут. КА удаляется от Земли на расстояние до
405 тыс. км. Подлет к Луне осуществляется по гиперболической селеноцентрической орбите, скорость «на бесконечности» V ¥ » 1 км/ c , скорость торможения при посадке D V 2 » 2600 м/ c .
На рис. 2 представлена схема траекторий полета советского КА «Луна-10», запущенного 31.03.1966 г. и выведенного впервые на орбиту искусственного спутника Луны (ИСЛ) 3.4.1966 г. [9]. Эта траектория имеет примерно те же характеристики, что и траектория КА «Луна-9», только после торможения получается не нулевая скорость, а эллиптическая для орбиты с периселением H p = 350 км, апоселением H a = 1017 км, поэтому скорость торможения меньше, D V 2 » 0,75 км/с.

В таблице 1 в первой колонке (прямой полет) приведены основные характеристики данного класса траекторий полета к Луне. Они осуществляются в гравитационном поле системы Земля – Луна, расстояния до Земли меняется до
400 тыс. км, время полета до Луны не превышает
5,4 сут. Захвата Луной нет, КА подлетает к Луне по гиперболе со скоростью V ¥ » 0,8 –
Источник
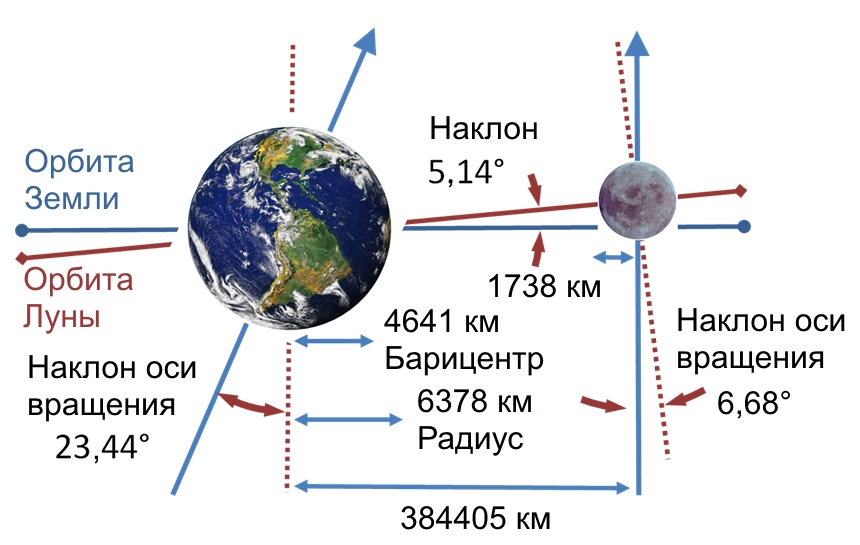
Расстояние от Земли до Луны
Луна с незапамятных времен была постоянным спутником нашей планеты и самым близким к ней небесным телом. Естественно, человеку всегда хотелось там побывать. Но далеко ли туда лететь и какое до нее расстояние?
Что такое
Расстояние от Земли до Луны теоретически измеряется от центра Луны до центра Земли. Измерить это расстояние обычными методами, используемыми в обычной жизни, невозможно. Поэтому дистанция до земного спутника вычислялась по тригонометрическим формулам.
Перигей и апогей Луны
Аналогично Солнцу, Луна испытывает постоянное движение на земном небе вблизи эклиптики. Тем не менее, это движение значительно отличается от движения Солнца. Так плоскости орбит Солнца и Луны различаются на 5 градусов. Казалось бы, вследствие этого траектория Луны на земном небе должна быть похожа в общих чертах на эклиптику, отличаясь от нее только сдвигом на 5 градусов:
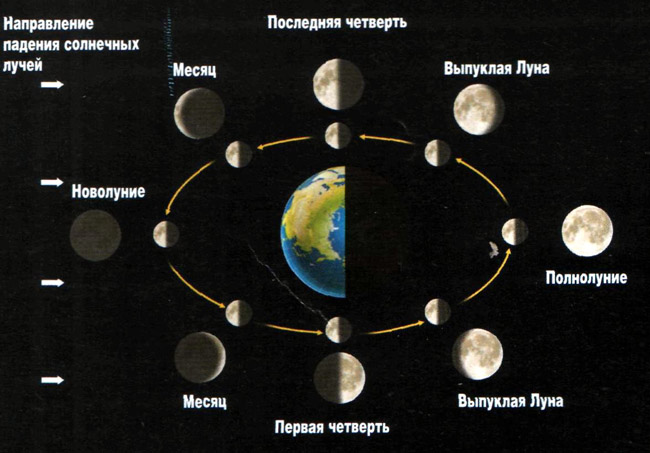
В этом движение Луна напоминает движение Солнца – с запада на восток, в противоположном направлении суточному вращению Земли. Но кроме того Луна движется по земному небу гораздо быстрее Солнца. Это связано с тем, что Земля совершает оборот вокруг Солнца примерно за 365 суток (земной год), а Луна вокруг Земли всего за 29 суток (лунный месяц). Это различие и стало стимулом к разбивке эклиптики на 12 зодиакальных созвездий (за один месяц Солнце смещается по эклиптике на 30 градусов). За время лунного месяца происходит полная смена фаз Луны:
В дополнение к траектории движения Луны добавляется ещё и фактор сильной вытянутости орбиты. Эксцентриситет орбиты Луны составляет 0.05 (для сравнения у Земли этот параметр равен 0.017). Отличие от круговой орбиты Луны приводит к тому, что видимый диаметр Луны постоянно меняется от 29 до 32 угловых минут.
В конечном итоге траектория положения Луны на земном небе постоянно мигрирует относительно фоновых звезд и эклиптики
За сутки Луна смещается относительно звезд на 13 градусов, за час примерно на 0.5 градусов. Современные астрономы часто используют покрытия Луны для оценок угловых диаметров звезд вблизи эклиптики.
От чего зависит движение Луны
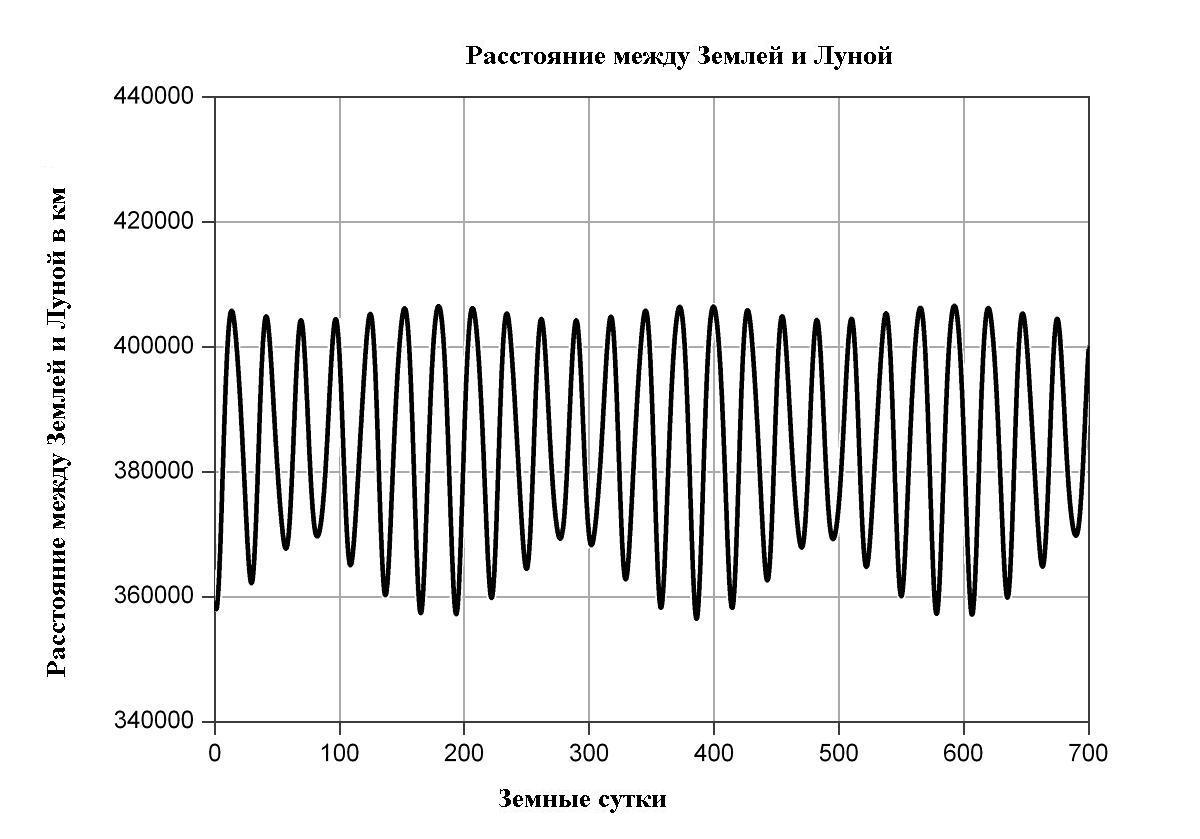
Важным моментом теории движения Луны является факт того, что орбита Луны в космическом пространстве не является неизменной и стабильной. По причине сравнительно небольшой массы Луны, она подвержена постоянным возмущениям от более массивных объектов Солнечной Системы (прежде всего Солнца и Луны). Кроме того, на орбиту Луны оказывают влияние сплюснутость Солнца и гравитационные поля других планет Солнечной Системы. В результате этого величина эксцентриситета орбиты Луны испытывает колебания между 0.04 и 0.07 с периодом в 9 лет. Следствием этих изменений стало такое явление, как суперлуние. Суперлунием называется астрономическое явление, в ходе которого полная луна в несколько раз больше по угловым размерам, чем обычно. Так во время полнолуния 14 ноября 2016 года Луна находилась на рекордно близком расстоянии с 1948 года. В 1948 году Луна была на 50 км ближе, чем в 2016 году.
Сравнение видимого диаметра Луны на земном небе в перицентре и апоцентре лунной орбиты
Кроме того наблюдаются и колебания наклонения лунной орбиты к эклиптике: примерно на 18 угловых минут каждые 19 лет.
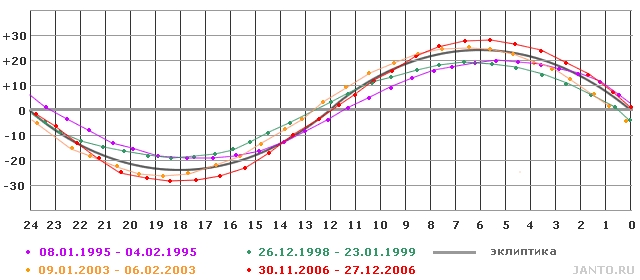
График изменения расстояния между Землей и Луной за 2 года
Чему равно
Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд
Космическим кораблям придется потратить на полет к земному спутнику немало времени. До Луны нельзя лететь по прямой – планета будет уходить по орбите в сторону от точки назначения, и путь придется корректировать. При второй космической скорости в 11 км/с (40 000 км/ч) полет теоретически займет около 10 часов, но на деле это будет происходить дольше. Все потому, что корабль на старте постепенно наращивает скорость в атмосфере, доводя ее до значения в 11 км/с, чтобы вырваться из поля тяготения Земли. Затем кораблю придется тормозить при подлете к Луне. Кстати, эта скорость- максимум, чего удалось добиться современным космическим кораблям.
Пресловутый полет американцев на Луну в 1969 году, согласно официальным данным, занял 76 часов. Быстрее всех до Луны удалось долететь аппарату НАСА «Новые горизонты» — за 8 часов 35 минут. Правда, он не приземлился на планетоид, а пролетел мимо – у него была другая миссия.
Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд. Но полеты на световых скоростях – пока что из области фантастики.
Можно попытаться представить путь до Луны в привычных величинах. Пешком при скорости 5 км/ч дорога до Луны займет порядка девяти лет. Если поехать на машине на скорость в 100 км/ч, то добираться до земного спутника придется 160 дней. Если бы на Луну летали самолеты, то рейс до нее продлился бы где-то 20 дней.
Как в древней Греции астрономы рассчитывали расстояние до Луны
Расстояние от Земли до Луны
Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.
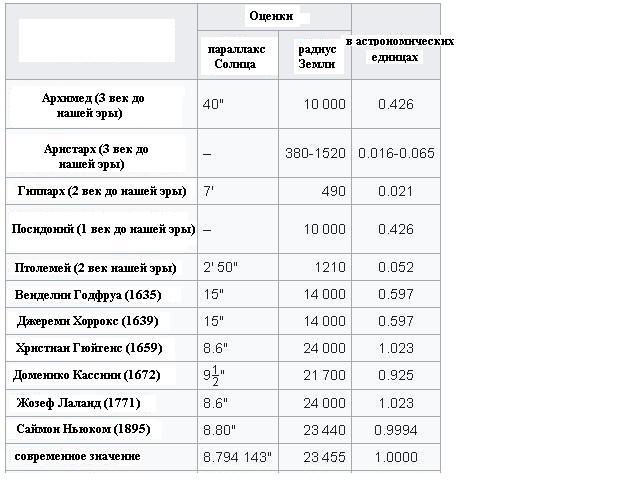
Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89.8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира. Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).
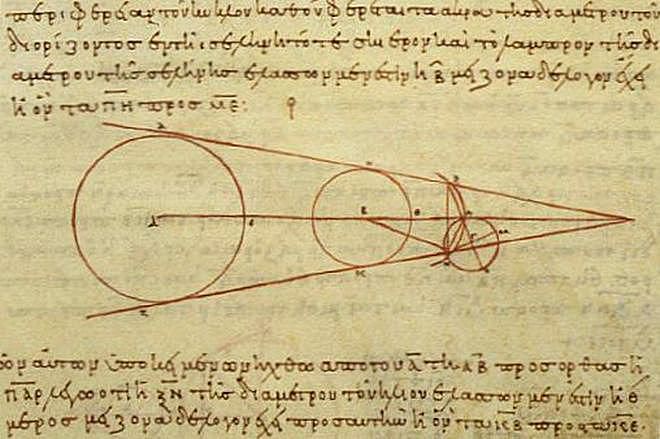
Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.
На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).
Чуть позже математик и астроном II века до н. э. Гиппарх Никейский подсчитал, что расстояние до земного спутника в 60 раз больше, чем радиус нашей планеты. Его расчеты основывались на наблюдениях за движением Луны и его периодических затмениях.
Материалы по теме
Наш естественный спутник Луна
Так как в момент затмения Солнце и Луна будут иметь одинаковые угловые размеры, то по правилам подобия треугольников можно найти отношение расстояний до Солнца и до Луны. Эта разница составляет 400 раз. Применяя еще раз эти правила, только уже по отношению к диаметрам Луны и Земли, Гиппарх вычислил, что диаметр Земли больше диаметра Луны в 2,5 раза. Т.е Rл = Rз/2,5.
Под углом в 1′ можно наблюдать предмет, размеры которого в 3 483 раза меньше, чем расстояние до него – эта информация во времена Гиппарха была всем известна. То есть, при наблюдаемом радиусе Луны в 15′ она будет ближе к наблюдателю в 15 раз. Т.е. отношение расстояния до Луны к ее радиусу будет равно 3483/15= 232 или Sл= 232Rл.
Соответственно, дистанция до Луны – это 232* Rз /2,5= 60 радиусов Земли. Это получается 6 371*60=382 260 км. Самое интересное, что измерения, выполненные при помощи современных инструментов, подтвердили правоту античного ученого.
Сейчас измерение дистанции до Луны проводится при помощи лазерных приборов, позволяющих измерить его с точностью до нескольких сантиметров. При этом измерения происходят за очень короткое время – не более 2 секунд, за которое Луна удаляется по орбите примерно на 50 метров от точки отправки лазерного импульса.
Эволюция методик измерения расстояния до Луны
Только с изобретением телескопа астрономы смогли получить более-менее точные значения параметров орбиты Луны и соответствия её размеров с размером Земли.
Пример эволюции астрономической единицы со временем
Более точный метод измерения расстояния до Луны появился в связи с развитием радиолокации. Первая радиолокация Луны была проведены в 1946 году в США и Великобритании. Радиолокация позволяла измерить расстояние до Луны с точностью в несколько километров.
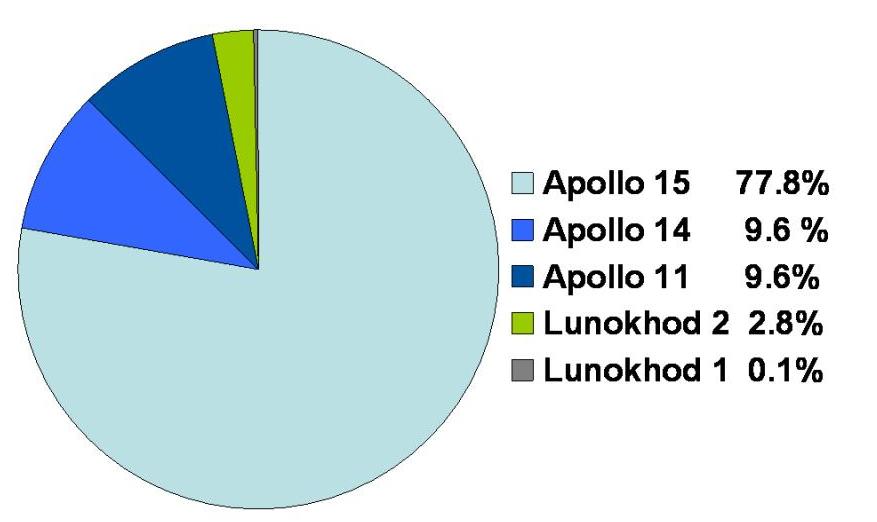
Ещё более точным методом измерения расстояния до Луны стала лазерная локация. Для его реализации в 1960х годах на Луне было установлено несколько уголковых отражателей. Интересно отметить, что первые эксперименты по лазерной локации были проведены ещё до установки уголковых отражателей на поверхности Луны. В 1962-1963 годах в Крымской обсерватории СССР были проведены несколько экспериментов по лазерной локации отдельных лунных кратеров с использованием телескопов диаметром от 0.3 до 2.6 метров. Эти эксперименты смогли определять расстояние до поверхности Луны с точностью в несколько сотен метров. В 1969-1972 годы астронавты программы “Аполлон” доставили на поверхность нашего спутника три уголковых отражателя. Среди них наиболее совершенным был отражатель миссии “Апполон-15”, так как он состоял 300 призм, тогда как два других (миссии “Апполон-11” и “Апполон-14”) только из ста призм каждый.
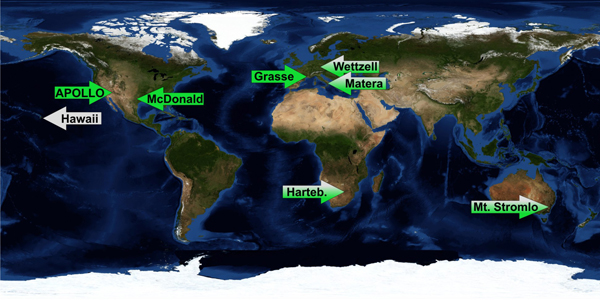
Карта положения уголковых отражателей
Кроме того в 1970 и 1973 годах СССР доставил на поверхность Луны ещё два французских уголковых отражателя на борту самоходных аппаратов “Луноход-1” и “Луноход-2”, каждый из которых состоял из 14 призм. Использование первого из этих отражателей обладает незаурядной историей. За первые 6 месяцев работы лунохода с отражателем удалось провести около 20 сеансов лазерной локации. Однако затем из-за неудачного положения лунохода вплоть до 2010 года не удавалось использовать отражатель. Лишь снимки нового аппарата LRO помогли уточнить положение лунохода с отражателем, и тем самым возобновить сеансы работы с ним.
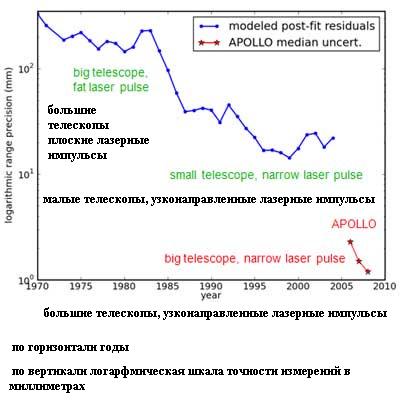
В СССР наибольшее количество сеансов лазерной локации было проведено на 2.6-метровом телескопе Крымской обсерватории. Между 1976 и 1983 годами на этом телескопе было проведено 1400 измерений с погрешностью в 25 сантиметров, затем наблюдения были прекращены в связи со свертыванием советской лунной программы.
Всего же с 1970 по 2010 годы в мире было проведено примерно 17 тысяч высокоточных сеансов лазерной локации. Большинство из них было связано с уголковым отражателем “Аполонна-15” (как говорилось выше, он является наиболее совершенным – с рекордным количеством призм):
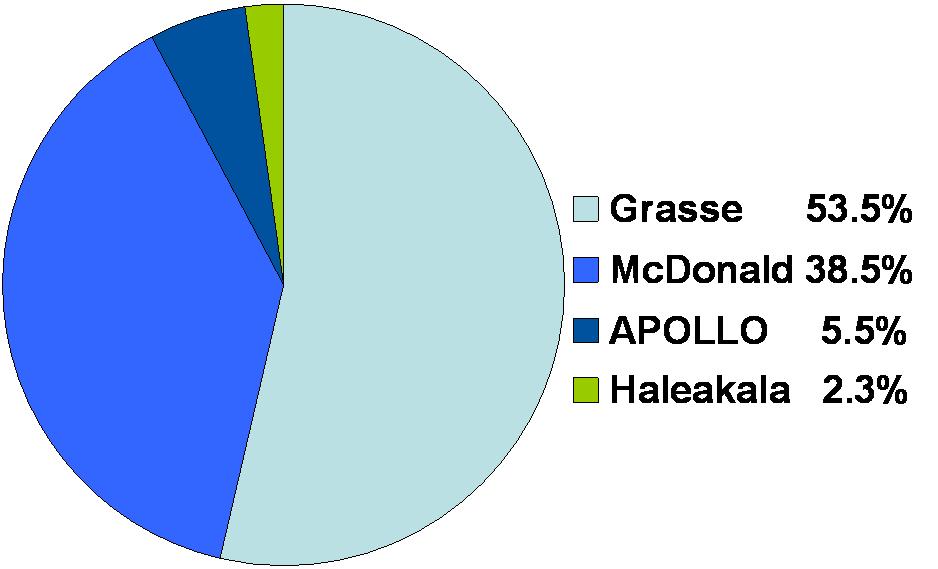
Из 40 обсерваторий, способных выполнять лазерную локацию Луны лишь несколько могут выполнять высокоточные измерения:
Большинство сверхточных измерений выполнено на 2-метровом телескопе в техасской обсерватории имени Мак Дональда:
В то же время наиболее точные измерения выполняет инструмент APOLLO, который был установлен на 3.5-метровом телескопе обсерватории Апач Пойнт в 2006 году. Точность его измерений достигает одного миллиметра:
 Эволюция системы Луна и Земля
Эволюция системы Луна и Земля
Главной целью всё более точных измерений расстояния до Луны являются попытки более глубокого понимания эволюции орбиты Луны в далеком прошлом и в отдаленном будущем. К настоящему времени астрономы пришли к выводу, что в прошлом Луна находилась в несколько раз ближе к Земле, а так же обладала значительно более коротким периодом вращения (то есть не была приливно захваченной). Этот факт подтверждает импактную версию образования Луны из выброшенного вещества Земли, которая преобладает в наше время. Кроме того, приливное воздействие Луны приводит к тому, что скорость вращения Земли вокруг своей оси постепенно замедляется. Скорость этого процесса составляет увеличение земных суток каждый год на 23 микросекунды. За один год Луна отдаляется от Земли в среднем на 38 миллиметров. Оценивается, что в случае если система Земля-Луна переживет превращение Солнца в красный гигант, то через 50 миллиардов лет земные сутки сравняются с лунным месяцем. В результате Луна и Земля будут всегда повернуты к друг другу только одной стороной, как сейчас наблюдается в системе Плутон-Харон. К этому времени Луна отдалится до, примерно, 600 тысяч километров, а лунный месяц увеличится до 47 суток. Кроме того, предполагается, что испарение земных океанов через 2.3 миллиардов лет приведет к ускорению процесса удаления Луны (земные приливы значительно тормозят процесс).
Кроме того, расчеты показывают, что в дальнейшем Луна снова начнет сближаться с Землей по причине приливного взаимодействия с друг другом. При приближении к Земле на 12 тысяч км Луна будет разорвана приливными силами, обломки Луны образуют кольцо наподобие известных колец вокруг планет-гигантов Солнечной Системы. Другие известные спутники Солнечной Системы повторят эту судьбу гораздо раньше. Так Фобосу отводят 20-40 миллионов лет, а Тритону около 2 миллиардов лет.
Интересные факты
Между Землей и Луной можно поместить все остальные планеты Солнечной системы
Каждый год расстояние до земного спутника возрастает в среднем на 4 см. Причины – движение планетоида по спиральной орбите и постепенно падающая мощность гравитационного взаимодействия Земли и Луны.
Между Землей и Луной теоретически можно разместить все планеты Солнечной системы. Если сложить диаметры всех планет, включая Плутон, то получится величина в 382 100 км.
‘ alt=»yH5BAEAAAAALAAAAAABAAEAAAIBRAA7 — Расстояние от Земли до Луны» title=»Расстояние от Земли до Луны»>
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Источник







 Эволюция системы Луна и Земля
Эволюция системы Луна и Земля