Определите центростремительное ускорение земли при ее движении вокруг солнца считайте орбиту земли

Считая орбиту земли окружностью определите модуль угловой

Определите центростремительное ускорение земли при её движении вокруг Солнца. Считайте орбиту Земли окружностью радиусом 1,5х10^8.

Ответ или решение 2

Найдите угловую и линейную скорости вращения Земли вокруг Солнца. Расстояние считайте равным 150 000 000 км.

Как найти угловую скорость

Значение угловой скорости вращения Земли вокруг Солнца можно рассчитать , не обращаясь к справочникам. Достаточно знать:

• чему равен угол, соответствующий одному полному обороту;
• что такое год;
• что такое угловая скорость.

Общеизвестно, что Земля делает полный оборот вокруг Солнца за один год. Полный оборот равен углу в ϕ = 2π радиан, и тогда угловая скорость ω = ϕ / t = 2π / T, где t – время поворота на угол ϕ.

Выходит, что угловая скорость ω = 2π рад/год.

Чтобы выразить угловую скорость в системе единиц СИ, найдем число секунд в году (1 год = 364,25 суток):

1 год = 364,25 * 24 часа = 364,25 * 24 * 60 минут = 364,25 * 24 * 60 * 60 секунд = 31471200 с.

Угловая скорость в радианах за секунду:

ω = 2π / T = 6,28 / 31 471 200 =1,995 * 10 -7 рад/с.

Значение угловой скорости в радианах за час:

ω = 2π / T = 6,28 / (364,25 * 24 ч) = 7,184 * 10 -4 рад/ч.

От угловой скорости к линейной

Знание угловой скорости позволяет легко рассчитать линейную скорость v:

v = ωR, где R – радиус орбиты.

• в километрах за секунду — v = 1,995 * 10 -7 рад/с * 150 000 000 км = 29,93 км/с;
• в километрах за час — v = 7,184 * 10 -4 рад/ч * 150 000 000 км = 107 755,7 км/ч
• в метрах за секунду — v = 1,995 * 10 -7 рад/с * 150 000 000 000 м = 29 932,13 м/с.

Получается, что линейная скорость Земли на орбите в 90 раз превышает скорость звука в воздухе.

Ответ: Угловая скорость ω = 1,995 * 10 -7 рад/с, линейная скорость v = 29 932,13 м/с.

Скорость обращения Земли вокруг Солнца — один полный оборот за год. Нужно выразить эту скорость в единицах СИ.

Один полный оборот соответствует углу Δφ = 2 * п = 2 * 3,14 рад.

Число секунд в году:

Δt = 364 сутки * 24 ч/сутки * 3600 с/ч = 31449600 с.

ω =Δφ / Δt = 2 * 3,14 / 31449600 с = 1,998*10-7 рад/с-1.

Линейная скорость v:

v= ωR = 1,998 * 10-7 с-1 * 150 000 000 000 м = 29 600 м/с.

Ответ: Угловая скорость — 1,998*10-7 рад/с, линейная скорость — 29 600 м/с.

Движение нашей планеты в космическом пространстве можно охарактеризовать двумя типами вращения: вокруг собственной оси и вокруг Солнца. В данной статье рассматривается понятие угловой скорости, приводятся необходимые формулы для вычисления этой величины, а также дается расчет скорости угловой вращения Земли вокруг своей оси и вокруг нашей звезды.

Что такое угловая скорость вращения?

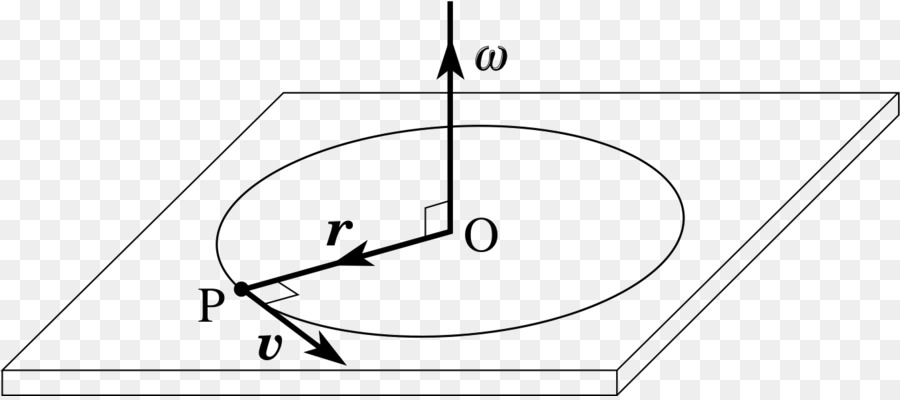
Когда рассматривают перемещение тела в пространстве на большие расстояния, то, как правило, пренебрегают его размерами. В этом случае вводят понятия пути и скорости его движения. Если же решают задачу движения тела вокруг некоторой точки или оси вращения, то пройденный путь всегда равен длине соответствующей окружности, а линейная скорость перемещения заменяется использованием скорости угловой.

Угловая скорость вращения представляет собой угол, на который тело поворачивается вокруг соответствующей оси за единицу времени. Исходя из этого определения, единицей измерения рассматриваемой величины будут радианы в секунду (рад/с). Также можно использовать градусы в секунду (˚/c). Обозначается угловая скорость греческой буквой омега ω.

Основные формулы

Прежде чем переходить к вопросу, чему равна скорость вращения Земли угловая, следует познакомиться с основными формулами, описывающими эту величину.

Как известно, угловая мера всей окружности составляет 360 ˚ или 2×π радиан, где π = 3,1416. Если тело совершает вокруг оси полный оборот за время T, тогда можно записать следующее выражение:

Время T называют периодом обращения, а величина f = 1/T показывает, сколько оборотов тело сделает за единицу времени, то есть характеризует частоту его вращения.

Еще одной важной формулой для угловой скорости является выражение, объединяющее линейную скорость и радиус вращения:

Если проверить единицу измерения ω в этом выражении, то получаем те же радианы в секунду (с -1 ). Формула показывает, что чем меньше расстояние от оси вращения до тела (r), и чем больше его скорость линейная (v), тем больше будет ω.

Из этой формулы можно легко выразить величину v: v = ω×r. Поскольку угловая скорость является величиной постоянной для некоторого рассматриваемого тела, то быстрее будут двигаться те точки, которые находятся дальше от оси вращения.

Рассмотренные формулы и понятия используем для определения скорости угловой вращения Земли вокруг оси и вокруг Солнца.

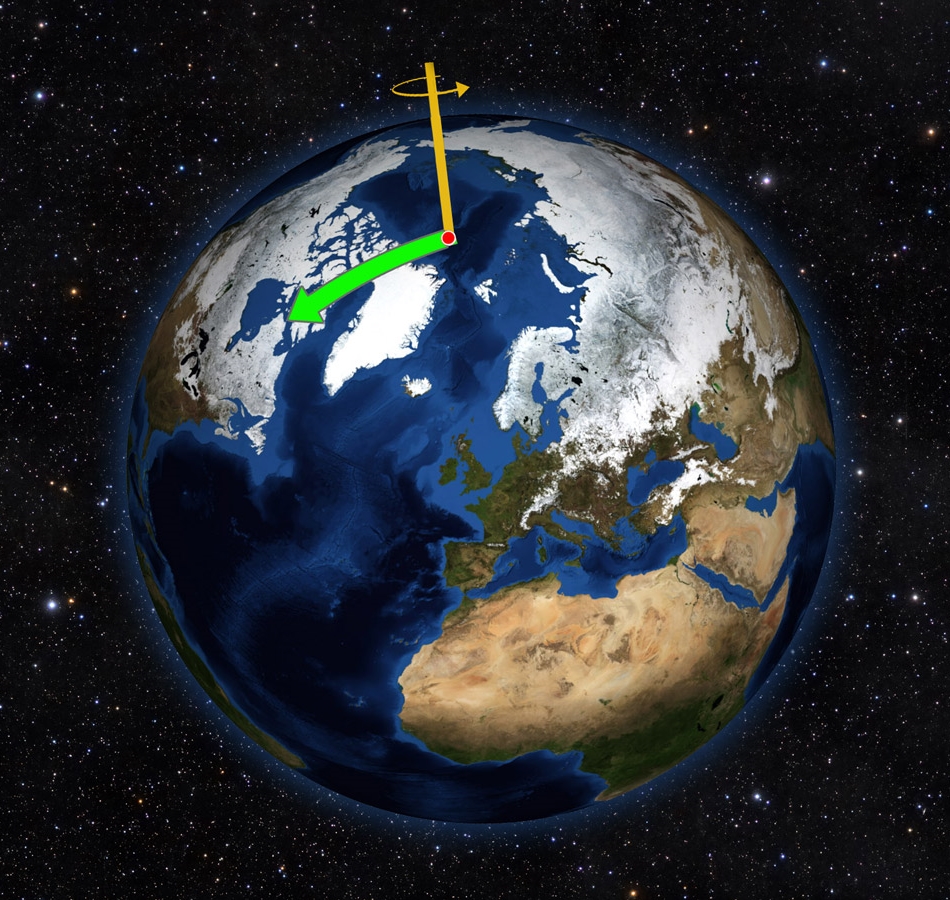
Вращение нашей планеты вокруг оси

Каждый человек знает, что планета, на которой он живет, вращается вокруг своей оси, причем экваториальная плоскость Земли наклонена под углом 23˚ к плоскости эклиптики.

Как рассчитать угловую скорость вращения вокруг своей оси Земли? Для этого можно воспользоваться совершенно любой из формул, которые приведены были выше. Поскольку мы знаем, что один оборот вокруг оси происходит за 24 часа, то для расчета следует использовать выражение с периодом T. Получаем:

Здесь значение периода T было переведено в секунды. Полученное значение является небольшим.

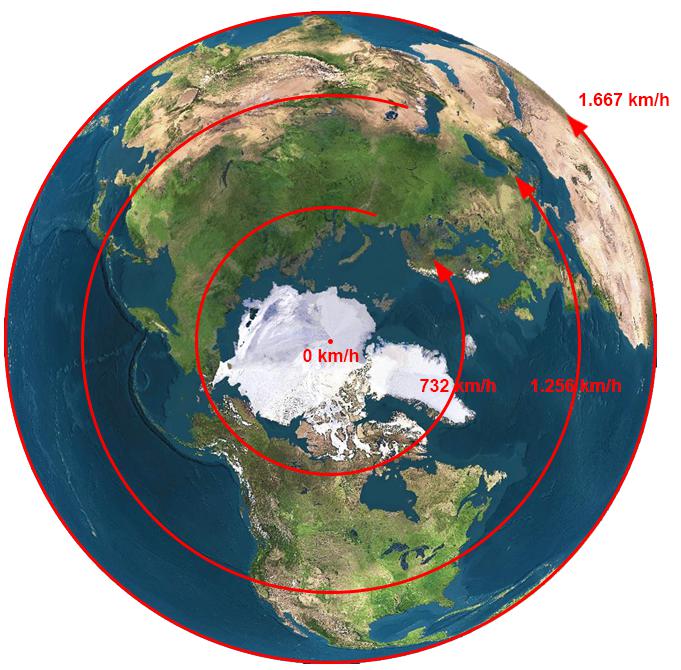
Представляет интерес рассчитать, с какой линейной скоростью движутся точки на поверхности планеты на широте 0˚ (экватор). Экваториальный радиус Земли равен 6 378 000 м. Подставляя это значение в формулу для скорости, получим:

v = ω×r = 7,27×10 -5 ×6 378 000 = 463,8 м/с = 1670 км/ч.

Полученное значение является большим в сравнении со скоростями, которые мы наблюдаем в жизни. Человек эту скорость не ощущает, поскольку вращается вместе с воздухом и почвой под ногами с одной скоростью, то есть он покоится относительно них.

Рассмотренное вращение Земли приводит не только к возникновению явления дня и ночи, но и к появлению так называемой силы Кориолиса, которая оказывает влияние на некоторые земные процессы, например, изменяет направление ветров.

Вращение Земли по своей орбите

Рассчитаем теперь угловую скорость вращения Земли вокруг Солнца. Для этого воспользуемся следующими данными: точное значение сидерического периода обращения нашей планеты по орбите составляет 365 дней 6 часов 9 минут и 9,7632 секунды, то есть T = 31558149,7632 секунд. Теперь можно воспользоваться формулой:

ω = 2×π/T = 2×3,1416/(31558149,7632) = 1,991×10 -7 рад/с.

То есть угловая орбитальная скорость нашей планеты меньше на 1,5 порядка, чем аналогичная величина для вращения вокруг собственной оси. Вычислим линейную скорость, учитывая, что средний радиус орбиты равен 149 597 871 000 метров:

v = ω×r = 1,991×10 -7 ×149 597 871 000 = 29784,8 м/с = 107 225 км/ч.

С этой огромной скоростью наша планета движется в космическом пространстве вокруг Солнца.

С орбитальным движением планеты и наклоном ее оси связано существование времен года в Северном и Южном полушариях.

Источник

Задание 67

Физика А.В. Перышкин

1.Определите центростремительное ускорение Луны при её обращении вокруг Земли. Необходимые для решения задачи данные найдите самостоятельно.

2. Используя дополнительную литературу и ресурсы Интернета, подготовьте доклад на тему «Планеты-карлики в Солнечной системе».

Карликовые планеты Солнечной системы — сравнительно новое понятие в классификации планет. Введено в 2006 году, после открытия Эриды.

По первоначальным данным, оказалось, что Эрида больше Плутона. В печати появились сообщения об открытии десятой планеты Солнечной системы. Потом последовали то опровержения, то подтверждения этого. Возникла неопределённость: что же всё-таки открыли — астероид или планету? Вдобавок, Плутон имеет всё-же довольно небольшой размер и ранее иногда возникали вопросы — считать его планетой или нет. Понятие «малая планета» тоже не подходило — к ним относятся и небольшие тела вроде Эроса и более внушительные, такие как Церера.
Поэтому было решено ввести новое понятие — карликовая планета Солнечной системы. Поскольку пока неясно, будет ли оно применяться к другим звёздным системам.

Для того, чтобы считаться карликовой планетой, небесное тело должно отвечать следующим условиям:
1) обращаться по собственной орбите вокруг Солнца, то есть тело не должно быть спутником планеты;
2) масса и создаваемая ею сила гравитации должны быть достаточны для поддержания гидростатического равновесия и иметь форму близкую к округлой;
3) в то же время, масса и гравитация недостаточны для доминирования на своей орбите и расчистки прилегающего пространства от других объектов.

В итоге, без вины виноватый Плутон больше не является планетой — его «разжаловали» в карликовые планеты Солнечной системы.

Стоит отметить, что эти требования всё-же страдают неопределённостью.
Например, если вдруг окажется, что Меркурий не смог до конца очистить свою орбиту и рядом с ним существует какой-то маленький астероид, не открытый пока из-за трудности наблюдений вблизи Солнца, то возникнет вопрос о переводе Меркурия в группу карликовых планет. (вероятность этого близка к нулю — приведено просто как пример).
Или напротив — объект больше Меркурия и по размерам, и по массе, имеющий округлую форму, но находящийся крайне далеко от Солнца не успел пока до конца расчистить свою орбиту вследствие крайне большого периода обращения вокруг Солнца. В пределы его орбиты мог «недавно» залететь астероид и остаться на этой новой орбите — из-за большого периода обращения, у планеты-хозяйки до него просто пока «не дошли руки». И тогда полноценная планета будет считаться карликовой!
Опять же, состав астероидов может быть самый разный, поэтому условия для гидростатического равновесия могут сильно различаться. Поэтому масса и размеры тоже могут колебаться в широких пределах. Тогда ледяная менее округлая громадина будет малой планетой, а гораздо меньшая по размеру, но более тяжёлая скала из горных пород получит более высокий статус карликовой планеты.
Поэтому многие астрономы до сих пор остаются несогласны с новой классификацией.

Сейчас к карликовым планетам Солнечной системы относят пять небесных тел:
Плутон, Хаумеа, Макемаке, Эрида и Церера.
Кроме них существуют ещё довольно много кандидатов на статус карликовой планеты Солнечной системы.
Во-первых, это три малых планеты из Главного пояса астероидов: Веста, Гигея и Паллада. Пока степень их гидростатического равновесия недостаточно известна. Недостающие данные о Весте должны были быть получены в 2011 году при исследовании Весты космическим аппаратом АМС Dawn (NASA), который вышел на её орбиту 16 июля 2011 года. На снимках видно, что форма этой карликовой планеты действительно близка к шарообразной, но об изменении статуса Весты пока не слышно.
Во-вторых, это уже известные объекты Рассеянного диска и пояса Койпера: Седна, Квавар, Варуна, Орк и другие. Вследствие их удалённости, пока нет точных данных об их массе и степени округлости.

Источник

Определите центростремительное ускорение земли при ее движении вокруг солнца считайте орбиту земли

В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли увеличивается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения по орбите и период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

3) не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

На спутник действует только сила притяжения со стороны Земли. Второй закон Ньютона приобретает вид: Отсюда видно, что если центростремительное ускорение увеличивается, то радиус орбиты уменьшается. Подставляя во второй закон Ньютона выражение для центростремительного ускорения имеем: Следовательно, в результате перехода на новую орбиту скорость движения спутника по орбите увеличивается. Период обращения спутника связан с радиусом орбиты и скоростью движения соотношением Так как радиус уменьшается, а скорость возрастает, получаем, что период обращения спутника вокруг Земли уменьшается.

Источник