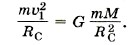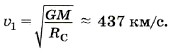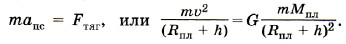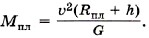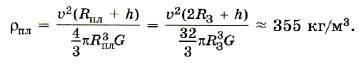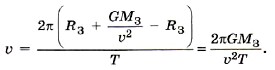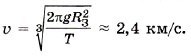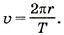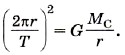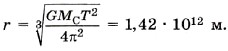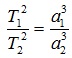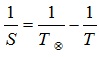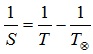§ 32. Примеры решения задач по теме «Первая космическая скорость
Для решения задач требуется знать закон всемирного тяготения, закон Ньютона, а также связь линейной скорости тел с периодом их обращения вокруг планет. Обратите внимание на то, что радиус траектории спутника всегда отсчитывается от центра планеты.
Задача 1. Вычислите первую космическую скорость для Солнца. Масса Солнца 2 • 10 30 кг, диаметр Солнца 1,4 • 10 9 м.
Р е ш е н и е. Спутник движется вокруг Солнца под действием единственной силы — силы тяготения. Согласно второму закону Ньютона запишем:
Из этого уравнения определим первую космическую скорость, т. е. минимальную скорость, с которой надо запустить тело с поверхности Солнца, чтобы оно стало его спутником:
Задача 2. Вокруг планеты на расстоянии 200 км от её поверхности со скоростью 4 км/с движется спутник. Определите плотность планеты, если её радиус равен двум радиусам Земли (Rпл = 2R3).
Р е ш е н и е. Планеты имеют форму шара, объём которого можно вычислить по формуле 
тогда плотность планеты
где Мпл — масса планеты, Rпл — её радиус.
Спутник движется вокруг планеты по круговой орбите. На него действует сила тяготения Fтяг, которая определяет центростремительное ускорение.
Согласно второму закону Ньютона
Из последнего уравнения находим массу планеты: 
Подставив это выражение в формулу (1), имеем
Задача 3. При какой скорости спутника период его обращения вокруг Земли равен двум суткам?
Р е ш е н и е. Скорость спутника
где h — высота спутника над поверхностью Земли.
Для определения скорости необходимо знать высоту h.
Спутник движется по круговой орбите, при этом сила тяготения является центростремительной силой. Согласно второму закону Ньютона для спутника запишем:
где m — масса спутника.
Из уравнения (2) находим высоту 
Подставим выражение для h в формулу (1) и из полученного уравнения определим искомую скорость:
Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда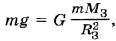 
отсюда GM3 = gR 2 3.
Подставив найденное выражение в формулу (3), определим скорость:
Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:
где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна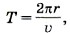 
отсюда 
Подставив выражение для скорости υ в уравнение (4), получим 
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца: 
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Все мы гении. Но если вы будете судить рыбу по её способности взбираться на дерево, она проживёт всю жизнь, считая себя дурой.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
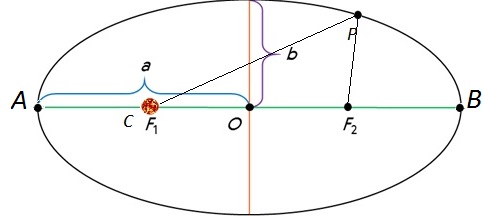
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
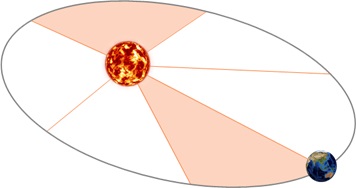
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
,
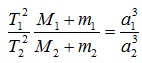
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
,
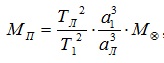
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
Примеры решения задач по теме: Первая космическая скорость
Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 
отсюда GM3 = gR 2 3.
Подставив найденное выражение в формулу (3), определим скорость:
Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:
где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна 
отсюда 
Подставив выражение для скорости υ в уравнение (4), получим 
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца: 
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С 1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С 2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С 3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С 4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
С 5. С какой скоростью движутся частицы, входящие в наиболее плотное кольцо Сатурна, если известно, что период их обращения примерно совпадает с периодом вращения Сатурна вокруг своей оси и составляет 10 ч 40 мин? Масса Сатурна равна 5,7 • 10 26 кг.
Источник