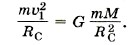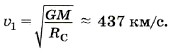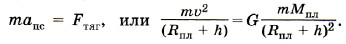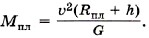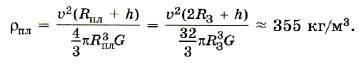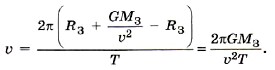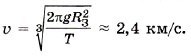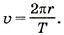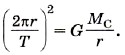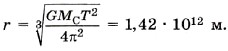Как измерить массу Земли и массу Солнца?
Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами
Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.
На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений
С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.
Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.
Для начала измерим массу Земли
Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.
Принцип этого определения следующий:
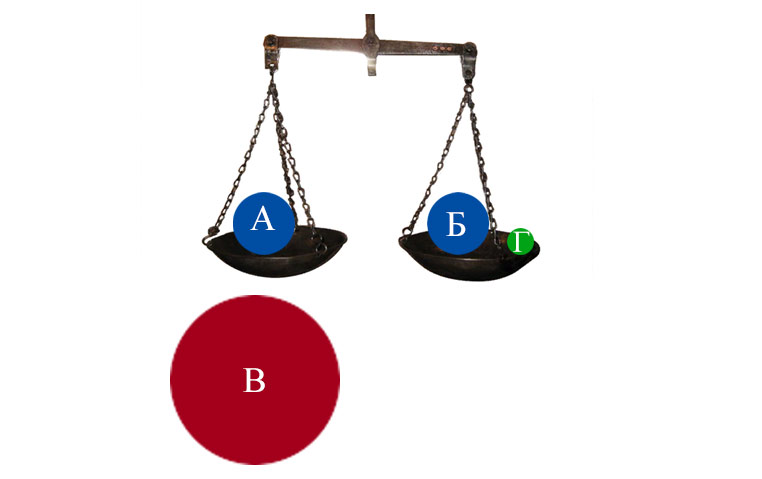
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.
Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.
Как вычислить массу планеты Земля, не выходя из дома?
Вас может заинтересовать
А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.
А теперь измерим массу Солнца!
Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.
Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.
Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.
Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.
Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра
Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.
Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.
Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.
Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.
Источник
2. Суть законов Кеплера, и их связь с законом всемирного тяготения. Насколько применима модель, принятая Ньютоном? Определите массу солнца если известно что Земля движется вокруг него со скоростью 30 км/с на среднем расстоянии 150 млн.км.
Первый закон Кеплера. Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце. Второй закон Кеплера Радиус-вектор планет за равные промежутки времени описывают равные площади. Третий закон Кеплера. Квадраты периодов обращения двух планет относятся как кубы больших полуосей их орбит. Законы Кеплера применимы не только к движению планет, но и к движению их естественных и искусственных спутников. Кеплеровские законы были уточнены и объяснены на основе закона всемирного тяготения Исааком Ньютоном. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделённых расстоянием R есть , Здесь G — гравитационная постоянная, равная — 6,673(10)*10 -11 мі/(кг сІ). Знак минус означает, что сила, действующая на тело, всегда противоположна по направлению радиус-вектору, направленному на тело, т. е. гравитационное взаимодействие приводит всегда к притяжению любых тел. Таким образом в формулировке Ньютона законы Кеплера звучат так:
первый закон: под действием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение.
формулирование второго закона Кеплера не дана, так как в этом не было необходимости.
третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет.
Из формул центробежной силы, закона всемирного тяготения выражаем массу Солнца. , . Центробежная сила Земли рассчитывается следующим образом: , где m — масса Земли; v — скорость движения Земли вокруг Солнца; к — радиус Земли. mEarth = 5.9*10 24 кг; Радиус Земли составляет 6358 км. F = 5.9*10 24 кг * 30000 м/с / 6358000 = 0,028*10 24 Н. Таким образом, масса Солнца = (0,028*1024 Н * 22500000 м2)/ (6.67·10-11 Нм2/кг2 * 5.9*1024кг) = 1 989 100*1024 кг.
Источник
Примеры решения задач по теме: Первая космическая скорость

Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 
Подставив найденное выражение в формулу (3), определим скорость:

Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:

где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна 
Подставив выражение для скорости υ в уравнение (4), получим
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца:
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С 1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С 2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С 3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С 4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
С 5. С какой скоростью движутся частицы, входящие в наиболее плотное кольцо Сатурна, если известно, что период их обращения примерно совпадает с периодом вращения Сатурна вокруг своей оси и составляет 10 ч 40 мин? Масса Сатурна равна 5,7 • 10 26 кг.
Источник
§ 32. Примеры решения задач по теме «Первая космическая скорость
Для решения задач требуется знать закон всемирного тяготения, закон Ньютона, а также связь линейной скорости тел с периодом их обращения вокруг планет. Обратите внимание на то, что радиус траектории спутника всегда отсчитывается от центра планеты.
Задача 1. Вычислите первую космическую скорость для Солнца. Масса Солнца 2 • 10 30 кг, диаметр Солнца 1,4 • 10 9 м.
Р е ш е н и е. Спутник движется вокруг Солнца под действием единственной силы — силы тяготения. Согласно второму закону Ньютона запишем:
Из этого уравнения определим первую космическую скорость, т. е. минимальную скорость, с которой надо запустить тело с поверхности Солнца, чтобы оно стало его спутником:
Задача 2. Вокруг планеты на расстоянии 200 км от её поверхности со скоростью 4 км/с движется спутник. Определите плотность планеты, если её радиус равен двум радиусам Земли (Rпл = 2R3).
Р е ш е н и е. Планеты имеют форму шара, объём которого можно вычислить по формуле 
где Мпл — масса планеты, Rпл — её радиус.
Спутник движется вокруг планеты по круговой орбите. На него действует сила тяготения Fтяг, которая определяет центростремительное ускорение.
Согласно второму закону Ньютона
Из последнего уравнения находим массу планеты:
Подставив это выражение в формулу (1), имеем
Задача 3. При какой скорости спутника период его обращения вокруг Земли равен двум суткам?
Р е ш е н и е. Скорость спутника
где h — высота спутника над поверхностью Земли.
Для определения скорости необходимо знать высоту h.
Спутник движется по круговой орбите, при этом сила тяготения является центростремительной силой. Согласно второму закону Ньютона для спутника запишем:
где m — масса спутника.
Из уравнения (2) находим высоту 
Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 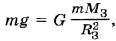
Подставив найденное выражение в формулу (3), определим скорость:
Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.
Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:
где m — масса Сатурна, r — расстояние от Сатурна до Солнца, Мс — масса Солнца.
Период обращения Сатурна 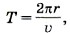
Подставив выражение для скорости υ в уравнение (4), получим
Из последнего уравнения определим искомое расстояние от Сатурна до Солнца:
Сравнив с табличными данными, убедимся в правильности найденного значения.
Задачи для самостоятельного решения
1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.
2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R3 + h на орбиту радиусом R3 + 2h, где высота h равна 200 км?
3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.
Образцы заданий ЕГЭ
С1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.
С2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υЗ/υЮ линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?
С3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?
С4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υп/υ3.
Источник