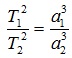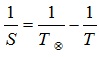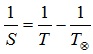Астрономия. Решение задач. Тема: Законы Кеплера
Из опыта работы
Тема : Законы Кеплера
Звездный период обращения Юпитера вокруг Солнца составляет около 12 лет. Каково среднее расстояние Юпитера от Солнца?
Среднее расстояние планеты от Солнца равно большой полуоси эллиптической орбиты a. Из третьего закона Кеплера


для определения среднего расстояния планеты от Солнца в астрономических единицах по известному звездному (сидерическому) периоду обращения, выраженному в годах. Подставив численные значения окончательно найдем:

Ответ: около 5 а.е.
Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а=2,88 а. е., а эксцентриситете =0,24
а=2,88 а.е
е=0,24
_________________________
Радиус перигелия рассчитывается по формуле: r=(1-e)а, где: a — большая полуось; е — эксцентриситет орбиты.
Афелий орбиты рассчитывается по формуле r =(1+е)а, где a — большая полуось; е — эксцентриситет орбиты.
r=2.88(1 +0,24)=3.57 а.е
Ответ: 3.57 а.е
Период обращения малой планеты Шагал вокруг Солнца Т=5,6 года. Определите большую полуось ее орбиты.

а1=Т1 2
а1=3√5,6 2 =3.2 а.е
Ответ: 3.2 а.е
Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а=160 млн км, а эксцентриситет е=0,83.
а = 160 млн. км
е = 0,83
_________________________
r=?
r=(1-e)а
r=1,6*10 8 (1-0,83)=2,72*10 7 км
Ответ: 2,72*10 7 км
просмотров всего 64,120 , просмотров сегодня 54
Источник
Урок 8
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
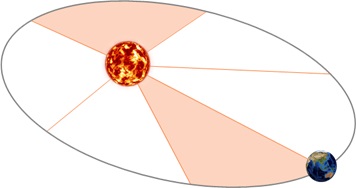
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
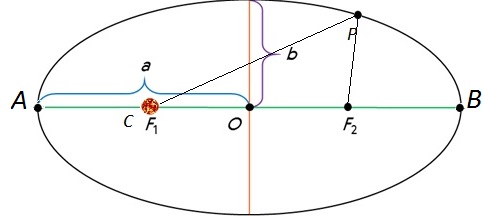
Перигелийное расстояние $ПС = q$; афелийное расстояние $СА = Q$. $АП = 2a$; $ПО = ОА = a$. Тогда: $q = ОП — СО$; $e = \dfrac<СО><ОП>$; $СО = e · a$; $Q = ОА + СО$; $q = a — ea = a(1 — e)$; $Q = a + ea = a(1 + e)$.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
- а) скорость планеты максимальна;
- б) потенциальная энергия максимальна;
- в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
- а) скорость планеты минимальна;
- б) потенциальная энергия минимальна;
- в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Решебник по астрономии 11 класс на урок №10 (рабочая тетрадь) — Определение расстояний до небесных тел в Солнечной системе и их размеров
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №10 (рабочая тетрадь) — Определение расстояний до небесных тел в Солнечной системе и их размеров
1. Закончите предложения.
Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.
1 а.е. = 149 600 000 км
Расстояние до объекта по времени прохождения радиолокационного сигнала можно определить по формуле , где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.
2. Дайте определения понятиям «параллакс» и «базис»; на рисунке 10.1 покажите эти величины.
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.
Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.
3. Как с помощью понятий параллакса и базиса определить расстояние до удаленного недоступного объекта С (рис. 10.1)?
По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.
4. Угол, под которым со светила S виден радиус Земли, перпендикулярный лучу зрения, называется горизонтальным параллаксом p (рис, 10.2). Определите расстояния: а) до Луны, если ее горизонтальный параллакс p = 57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″.
5. Дополните рисунок 10.3 необходимыми построениями и выведите формулу, позволяющую определить радиус небесного светила (в радиусах Земли), если известны угловой радиус светила p и его горизонтальный параллакс p.
r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ»/p» · R.
6. Решите следующие задачи (при расчетах считайте, что c = 3 · 10 5 км/с, R3 = 6370 км).
1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?
2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.
3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.
1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?
Ответ: 41 млн км.
2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?
Ответ: 1,22 млн км.
3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
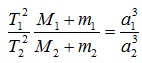
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
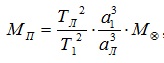
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
6. Выполните задание.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник