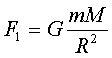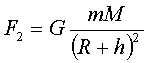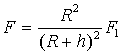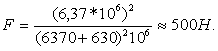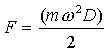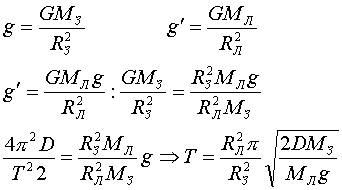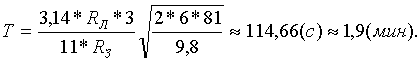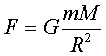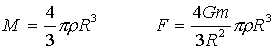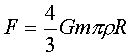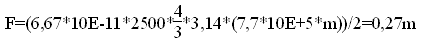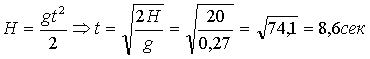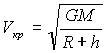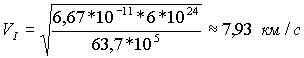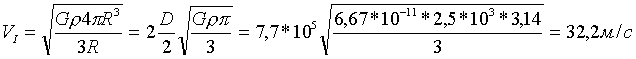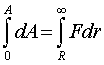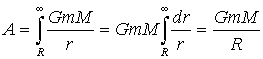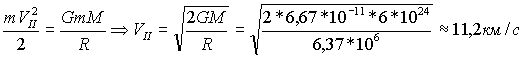Определить силу с которой солнце притягивает землю

Сила тяготения со стороны Земли, которая может быть выражена через ускорение свободного падения как F=mg, непостоянна и находится в зависимости от ряда факторов. Это нашло отражение в школьном курсе физики. Напомним, что сила гравитации, а, следовательно, и ускорение свободного падения являются функциями:

1. высоты поднятия тела над Землёй,
2. аномалии в строении земной поверхности,
3. широты местонахождения тела на поверхности Земли, что вызвано натуральной сплюснутостью, и эффектом осевого вращения нашей планеты. (1).

Одна из простейших задач на расчет силы тяжести может быть сформулирована следующим образом:

Задача 1. Определить силу, с которой Земля притягивает к себе тело, находящееся от нее на высоте 630 км, если сила тяготения близ поверхности Земли известна и равна 600 H. Радиус Земли считать равным 6370 км.

h=630 км.
R=6370 км.
F=600 H.

В соответствии с законом тяготения выражения силы тяжести для двух случаев могут быть записаны в скалярной форме:

Их отношение позволит легко определить значение искомой величины

и после подстановки данных

В качестве примера можно привести определение силы тяжести на земном спутнике, Луне, на одной из планет-гигантов или их спутниках, либо на одном из астероидов, воспользовавшись при этом конкретными сведениями о величинах поперечников рассматриваемых объектов, плотностей и их масс.

Задача 2. С каким периодом должен вращаться космический корабль диаметром 6м., чтобы космонавт чувствовал себя как в поле тяготения Луны, находясь на ее поверхности. Известны отношения масс, радиусов Земли и Луны (81 и 11/3 соответственно). Ускорение свободного падения на поверхности Земли считать известным.

Во вращающемся космическом корабле возникает сила F, прижимающая космонавта в направлении от оси вращения к стенке корабля. Эта сила есть результат ускоренного движения системы и связана с центростремительным ускорением знаком минус F = -ma,

где m — масса космонавта, a — центростремительное ускорение, равное w 2 r. Через диаметр выражение для F примет вид

В том случае, если космонавт находится в поле силы тяжести спутника Земли, последняя может быть представлена через ускорение свободного падения на поверхности Луны g ‘ . F=mg ‘ . Связывая два соотношения для силы F, будем иметь

В условии задачи известны отношения масс, радиусов планеты и спутника, а потому ускорение свободного падения на поверхности Луны найдется из отношения следующих выражений:

После подстановки данных

Задача 3. Астероид Церера (4) с средней плотностью вещества около 2500 кг/м 3 имеет размер поперечника 770 км. Зная массу своего тела, определите с какой силой притягивает вас к своей поверхности Церера. Как долго смогли бы вы падать на поверхность планеты с высоты 10м. (сравните с временем падения на Земли при g=9,81 м/с 2 ). Какую скорость, во-первых, необходимо сообщить телу на поверхности Цереры, и, во-вторых, вышло из поля гравитации планеты. (Цереру считать однородным шаром).

ρ=2500 кг/м 3
D=770 км=7,7*10 5 м
g=9,8 м/с 2 .
G=6,67*10 -11 Hм 2 /кг 2 .

Первых три вопроса не представляют трудности для их разрешения. Из закона тяготения следует, что

где M, R — масса и радиус астероида.

Масса Цереры легко рассчитывается через плотность и объем сферического тела.

В результате подстановки числовых данных будем иметь

Если учесть массу человека, скажем, в 60 кг., то F=16,2 H. Считая ускорение свободного падения близ поверхности планеты постоянным, можно, применив формулу пути равнопеременного движения, определить время, за которое свободно падающее без начальной скорости тело пройдет расстояние 10 метров.

Оно, оказывается в 6,02 раза больше времени падения тела на поверхности Земли.

Третий и четвертый вопросы преследуют цель нахождения первой и второй космической скоростей, с приобретением которых тела становятся либо искусственными спутниками планет, либо выходят из поля гравитации планет. Определение космических скоростей — это второй тип задач, предлагаемых вниманию читателя.

С процессом нахождения первой космической скорости тело относительно Земли учащийся хорошо знаком из курса физики средней школы. С одной стороны, центростремительное ускорение, сообщаемое движущемуся по круговой орбите телу силой земного притяжения,

, и с другой стороны,

, где R — радиус Земли, а скорость рассчитывается относительно поверхности Земли. Эта скорость и есть первая космическая.

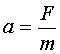
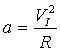
Расписывая силу земного тяготения, будем иметь

С увеличением высоты тела над Землей круговая скорость уменьшается и тем значительнее, чем больше h.

После подстановки данных в формулу для первой космической скорости получаем хорошо знакомую цифру

Для Цереры, в частности, первая космическая скорость примет значение:

Определение скорости освобождения тела из поля гравитации планеты или звезды ведется с позиции интегрального метода исчисления, с которым старшеклассник и, более того, студент ВУЗа хорошо знаком.

Рассуждаем следующим образом: кинетическая энергия, которую следует сообщить телу у поверхности Земли, должна полностью расходоваться на работу по преодолению сил земного тяготения
, где V_II — есть вторая космическая скорость.

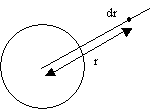
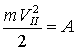
Поскольку сила тяжести переменна и зависит от расстояния до планеты, то рассчитать работу этой силы можно, выделив очень малый участок пути (dr), на котором направление, а также величину силы можно считать постоянной. Тогда элементарная работа на малом участке перемещения примет вид dA=Fdr. А полная работа определяется путем интегрирования

Пределы интегрирования выбраны с учетом того, что в начале пути тело находилось на поверхности Земли, а в конце ушло в бесконечность относительно поля земного тяготения.

Подставив в выражение для кинетической энергии вместо работы А, будем иметь для второй космической скорости значение

Относительно астероида Цереры вторая космическая скорость вычисляется согласно выражению:

Ввести определение скоростей космических объектов аналогичным образом можно, вкладывая в содержание задач несколько иной смысл.

Перечень предлагаемых задач может быть значительно расширен, и, естественно, в компетенции преподавателя видоизменить ассортимент как качественных, так и вычислительного характера примеров раздела небесной механики. Полагаем, что с привлечением рекомендуемого в данной работе типа задач существенно повысится интерес учащихся (студентов) к изучению темы «Всемирное тяготение» обязательных курсов физики, астрономии и факультативных курсов, спецкурсов в школе и ВУЗе, что приведет к интенсификации процесса усвоения материала.

Источник

Солнце, планеты и гравитация – описание, фото и видео

Гравитация — самая таинственная сила во Вселенной. Ученые до сих пор не знают ее природы. Но именно гравитация удерживает на орбитах планеты Солнечной системы. Не будь силы тяготения, планеты разлетелись бы от Солнца, как бильярдные шары от удара кием.

Гравитация – сила тяготения

Если же смотреть глубже, то станет ясно, что не было бы гравитации, не было бы и самих планет. Сила тяготения — притяжение материи к материи — это та сила, которая собрала вещество в планеты и придала им круглую форму.

Гравитация

Силы тяготения Солнца вполне хватает на то, что бы удерживать девять планет, десятки их спутников и тысячи астероидов и комет. Вся эта компания роем вращается вокруг Солнца, как мотыльки вокруг освещенного балкона. Если бы не было силы тяготения, эти планеты, спутники и кометы полетели бы каждый своим путем по прямой линии. Вместо этого они вращаются вокруг Солнца по своим орбитам, потому что Солнце силой своего притяжения постоянно искривляет их прямолинейную траекторию, притягивая к себе планеты, луны и кометы с астероидами.

Гравитация и расстояние между объектами

Планеты кружатся вокруг светила, подобно тому, как пони, катающие детей, ходят по кругу, привязанные к столбу в центре этого круга. Разница только в способе привязки. Космические тела привязаны к Солнцу невидимыми нитями гравитации. Правда, чем больше расстояние между объектами, тем меньше сила притяжения между ними. Солнце гораздо слабее притягивает планету Плутон, самую дальнюю в Солнечной системе, чем, скажем, Меркурий или Венеру. Сила гравитации уменьшается (или увеличивается) в зависимости от расстояния экспоненциально.

Что это значит? Если бы, например, Земля была удалена от Солнца в два раза больше, чем сейчас, то сила притяжения уменьшилась бы в четыре раза. Если увеличить расстояние между Солнцем и Землей в три раза, то сила тяготения уменьшилась бы в девять раз. И так далее. Если «отодвинуть» Землю достаточно далеко и свести практически к нулю силу тяготения, то Земля может разорвать путы солнечного притяжения и отправиться в самостоятельное межзвездное плавание.

Гравитация и масса тела

На силу гравитации влияет также масса тел, то есть количество вещества в них. Земля и Солнце взаимно притягивают друг друга, но поскольку масса Солнца намного больше, то оно притягивает Землю сильнее. Ученые считают, что гравитация формирует пространство, которое искривляется вокруг сгустков материи. Чем массивнее сгусток, тем больше искривляется пространство. Каким образом это происходит? Вместе с приятелем туго растяните на весу простыню. Положите на простыню тяжелый металлический шар. Простыня прогнется под тяжестью шара и примет его форму.

Если положить на простыню меньшие шары, то они скатятся к большому. По мнению ученых, нечто подобное происходит и со звездами. Они искривляют пространство, как шары простыню в вашем опыте, и заставляют другие объекты «скатываться» по направлению к ним.

Интересное видео о гравитации

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

Почему Земля не падает на Солнце?

Продолжаем менять наше восприятие реальности при помощи такого легального инструмента, как общая теория относительности. Ну и книги Хокинга «Мир в ореховой скорлупе».

В прошлых статьях мы говорили о зарождении теории относительности; о том, что предлагает физика для продления жизни; что будет, если путешествовать на волне света; и как общая теория относительности породила ядерное оружие.

• откуда берутся чёрные дыры;
• как меняется пространство-время под объектам;
• что было в начале жизни Вселенной и что происходит сейчас.

Проблемка: теория относительности не сходится с законом тяготения Ньютона!

Закон тяготения Ньютона говорит о том, что если перераспределить материю в одной части Вселенной, то гравитационное поле мгновенно изменится во всей Вселенной. Слово «мгновенно» неприменимо для теории относительности, потому что оно означает во-первых, распространение изменений со сверхсветовой скоростью, что невозможно; во-вторых, для слова «мгновенно» необходимо, чтобы время было абсолютно, едино для всех и вся во Вселенной, что также невозможно: время индивидуально, т. е. для каждого течёт по-своему, об этом мы говорили здесь .

Гравитация и ускорение эквивалентны

Примерно в 1911 году Эйнштейн понял, что есть тесная взаимосвязь между гравитацией и ускорением. Например, если тебя, дорогой читатель, поместить в небольшое замкнутое помещение без окон (что-то вроде кабины лифта), то ты не сможешь определить, стоит это помещение неподвижно на Земле или летит с ускорением в открытом космосе.

Эйнштейн подумал годик и понял, что гравитация и ускорение должны быть эквивалентны если пространство-время искривлено.

У Альберта был друг Марсель Гроссман. Он помог Эйнштейну изучить теорию искривлённых пространств, и в 1913 году они написали статью, где предположили, что гравитация — это искривление пространства-времени. Новая теория об искривлении пространства-времени стала называться Общей теорией относительности , а старая теория, не включающая пространство-время, стала называться Специальной теорией относительности.

Подтверждение Общей теории относительности

В 1919 году Артур Эдингтон поехал в Западную Африку для того, чтобы подтвердить Общую теорию относительности. 29 мая 1919 года застала солнечное затмение. Это позволило наблюдать смещение видимого положения звезды, свет от которой проходил вблизи Солнца. Искривление пространства-времени Солнцем вызвало отклонение света, исходящего от звезды, находящейся за Солнцем.

Таким образом, человечество узнало, что пространство-время не пассивный фон, на котором происходят события Вселенной, а непосредственный участник этих событий.

Почему Земля не улетает от Солнца?

Действительно, что держит её? Космос такой большой, а она застыла у одной звезды.

Представьте, что пространство-время — это ткань. Если натянуть ткань и положить на неё, допустим, монету, ткань под монетой прогнётся, образовав воронку. Точно так же Солнце и другие объекты, даже Земля, прогибают под собой «ткань» пространства-времени. Всё, что находится рядом с объектом, попадает в воронку. Так Земля находится рядом с Солнцем, потому что она находится в воронке, которую образовало Солнце в пространстве-времни.

Источник