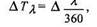1 Годовое движение Солнца и эклиптическая система координат
Солнце наряду с суточным вращением медленно в течение года перемещается по небесной сфере в противоположном направлении по большому кругу, называется эклиптикой. Эклиптика наклонена к небесному экватору под углом Ƹ, Величина которого в настоящее время близка к 23 26´. Эклиптика пересекается с небесным экватором в точке весеннего ♈ (21 марта) и осеннего Ω (23 сентября) равноденствий. Точки эклиптики, отстоящие от равноденственных на 90 , есть точки летнего (22 июня) и зимнего (22 декабря) солнцестояний. Экваториальные координаты центра солнечного диска непрерывно изменяются в течении года от 0h до 24 h (прямое восхождение) – эклиптическая долгота ϒm, отсчитывается от точки весеннего равноденствия до круга широты. И от 23 26´ до -23 26´ (склонение) – эклиптическая широта, отсчитывается от 0 до +90 к северному полюсу и 0 до -90 к южному полюсу. Зодиакальными созвездиями называются созвездия, которые находятся на линии эклиптики. Находится на линии эклиптики 13 созвездий: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей, Рыбы и Змееносец. Но созвездие Змееносца не упоминается, хотя Солнце и находится в нём большую часть времени созвездий Стрельца и Скорпиона. Сделано это для удобства. При нахождении Солнца под горизонтом на высотах от 0 до -6 — длятся гражданские сумерки, а от -6 до -18 — астрономические сумерки.
2 Измерение времени
Измерение времени основано на наблюдениях суточного вращения свода и годичного движения Солнца, т.е. вращения Земли вокруг своей оси и на обращении Земли вокруг Солнца.
Продолжительность основной единицы времени, называемой сутками, зависит от избранной точки на небе. В астрономии за такие точки принимаются:
— Точка весеннего равноденствия ♈ (звёздное время);
— Центр видимого диска Солнца (истинное Солнце, истинное солнечное время);
— среднее Солнце – фиктивная точка, положение которой на небе может быть вычислено теоретически для любого момента времени (среднее солнечное время)
Для измерения длинных промежутков времени служит тропический год, основанный на движении Земли вокруг Солнца.
Тропический год – промежуток времени, между двумя последовательными прохождениями центра истинного центра Солнца через точку весеннего равноденствия. Он содержит 365,2422 средних солнечных суток.
Из-за медленного движения точки весеннего равноденствия навстречу Солнцу, вызванного прецессией, относительно звёзд Солнце оказывается в той же точке неба через промежуток времени на 20 мин. 24 сек. больший, чем тропический год. Он называется звёздным годом и содержит 365,2564 средних солнечных суток.
3 Звёздное время
Промежуток времени между двумя последовательными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане называется звёздными сутками.
Звёздное время измеряется часовым углом точки весеннего равноденствия: S=t♈, и равно сумме прямого восхождения и часового угла любой звезды: S = α + t.
Звёздное время в любой момент равно прямому восхождению какого — либо светила плюс его часовой угол.
В момент верхней кульминации светила его часовой угол t=0, а S = α.
4 Истинное солнечное время
Промежуток времени между двумя последовательными кульминациями Солнца (центра солнечного диска) на одном и том же географическом меридиане называется истинными солнечными сутками.
За начало истинных Солнечных суток на данном меридиане принимают момент нижней кульминации Солнца (истинная полночь).
Время, протекающее от нижней кульминации Солнца до любого другого его положения, выраженное в долях истинных солнечных суток называется истинным солнечным временем Тʘ
Истинное солнечное время выражается через часовой угол Солнца, увеличенный на 12 часов: Тʘ = tʘ + 12 h
5 Среднее солнечное время
Для того, чтобы сутки имели постоянную продолжительность и при этом были связаны с движением Солнца, в астрономии введены понятия двух фиктивных точек:
— средне эклиптического и средне экваториального Солнца.
— Среднее эклиптическое Солнце (ср.эклип.С.) равномерно движется по эклиптике со средней скоростью.
— Среднее экваториальное Солнце движется по экватору с постоянной скоростью среднего эклиптического Солнца и одновременно с ним проходит точку весеннего равноденствия.
Промежуток времени между двумя последовательными кульминациями среднего экваториального Солнца на одном и том же географическом меридиане, называется средними солнечными сутками.
Время, протекающее от нижней кульминации среднего экваториального Солнца до любого другого его положения, выраженное в долях средних солнечных суток называется средним солнечным временем Тm.
Средне солнечное время Тm на данном меридиане в любой момент численно равно часовому углу Солнца: Тm = tm + 12 h
6 Всемирное, поясное и декретное время
Местное среднее солнечное время гринвичского меридиана называется всемирным или мировым временем Т0.
Местное среднее солнечное время любого пункта на Земле определяется: Тm= Т0 + λ h
Счёт времени ведётся на 24 основных географических меридиана, расположенных друг от друга на долготе точно через 15 (или 1 час) приблизительно посредине каждого часового пояса. Основным нулевым меридианом считается гринвичский. Поясное время есть всемирное время плюс номер часового пояса: ТП= Т0 + n
В России в практической жизни до марта 2011 г. использовалось декретное время:
Декретное время второго часового пояса, в котором располагается Москва, называют московским временем. В летний период (апрель-октябрь) стрелки часов переводились на час вперёд, а в зимний возвращались на час назад.
7 Рефракция
Видимое положение светил над горизонтом отличается от вычисленного по формулам. Лучи от небесного объекта, прежде чем попасть в глаз наблюдателя, проходят сквозь атмосферу Земли и преломляются в ней. И так ка плотность увеличивается к поверхности Земли, то луч света всё более отклоняется в одну и ту же сторону по кривой линии, так что направление ОМ1, по которому наблюдатель видит светило, оказывается отклонённым в сторону зенита и не совпадает с направлением ОМ2, по которому бы он видел светило при отсутствии атмосферы.
Явление преломления световых лучей при прохождении земной атмосферы называется астрономической рефракцией. Угол М1ОМ2 называют углом рефракции или рефракцией ρ.
Угол ZOM1 называется видимым зенитным расстоянием светила zʹ, а угол ZOM2 – истинным зенитным расстоянием z: z — zʹ = ρ, т.е. истинное расстояние светила больше видимого на величину ρ.
На линии горизонта рефракция в среднем равна 35ʹ.
Вследствие рефракции наблюдаются изменения формы дисков Солнца и Луны при их восходе или заходе.
Источник
МОРСКИЕ АСТРОНОМИЧЕСКИЕ ЕЖЕГОДНИКИ (МАЕ)



МОРСКИЕ АСТРОНОМИЧЕСКИЕ ПОСОБИЯ И ИНСТРУМЕНТЫ
Лекция№6
Основная формула времени
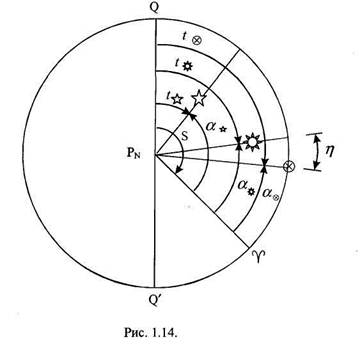
На сфере показана точка Овна (Y) и среднее Солнце (®), которые всегда находятся на небесном экваторе, а также истинное Солнце и звезда. На рисунке показаны часовые углы и прямые восхождения светил, а также часовой угол точки Овна, который является звездным временем
Дуга небесного экватора между меридианами истинного и среднего Солнца (77) — уравнение времени. Уравнение времени показывает, на сколько истинное время отличается от среднего. Значение уравнения времени на каждые сутки приводится в МАЕ.
— Непосредственно на чертеже видно, что часовой угол и прямое восхождение каждого светила в сумме дают звёздное время. Таким образом,
 |
Это уравнение называется основной формулой времени. Основная формула времени очень важна. Она связывает координаты первой и второй экваториальной системы и используется при расчёте часовых углов звёзд. Если в формуле (1.12) прямое восхождение заменить на 360°-Т, получим формулу для вычисления часовых углов звёзд:
Из формулы (1.12) следует, что в момент верхней кульминации светила его прямое восхождениеравно звёздному времени. Это обстоятельство используется на астрономических обсерваториях при определении прямых восхождений светил. В момент верхней кульминации замечается звёздное время и после исправления всеми поправками получают прямое восхождение светила.
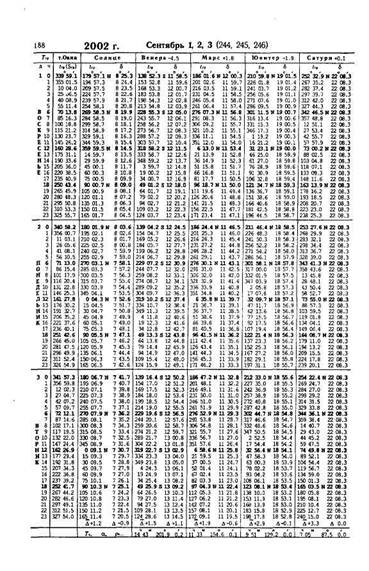
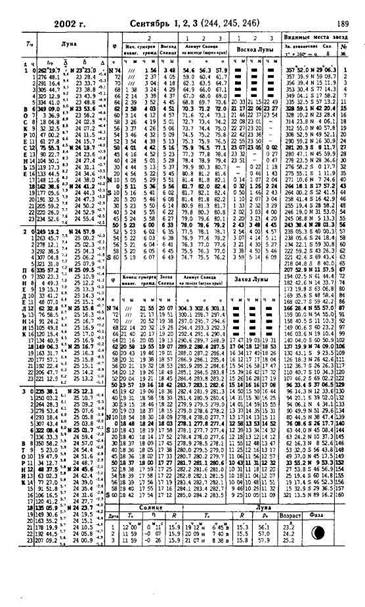
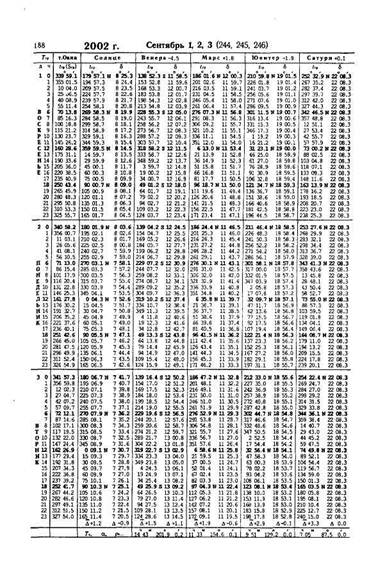
В морских астрономических ежегодниках собраны сведения о координатах светил, времени их кульминации, восходе, заходе, параллаксе, полудиаметре, азимуте восхода и захода Солнца и другие сведения. Координаты светил, предвычисленные наперёд, называются эфемеридами. Эфемериды Солнца, Луны и четырёх навигационных планет: Венеры, Марса, Юпитера и Сатурна даны на каждый час гринвичского времени. Эфемериды 67 наиболее ярких звезд (звёздные дополнения и склонения) даны в ежедневных таблицах. Кроме того, эфемериды 160 навигационных звезд на первое число каждого месяца сведены в отдельную таблицу «Видимые места звёзд».
Как следует из названия, ежегодники издаются на каждый год. Один разворот ежегодника содержит эфемериды и другие сведения на трехдневный интервал. Образец такого разворота, называемого ежедневными таблицами, приведён в прил.1.
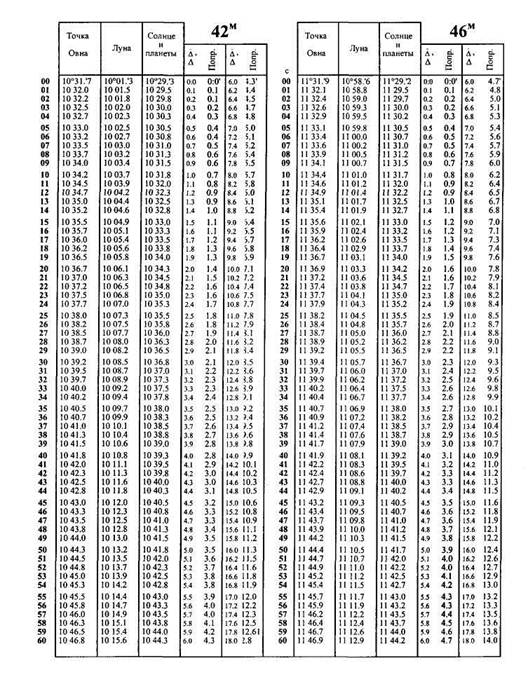
Аргументом для входа в ежедневные таблицы является название светила, гринвичская дата и гринвичское время. Эфемериды Солнца, Луны и планет, а также звёздное время даны на каждый час. Интерполяция на минуты и секунды делается с помощью основных интерполяционных таблиц, образцы которых приведены в прил. 2.
Помимо ежедневных таблиц и видимых мест звёзд, в МАЕ включены специально рассчитанные таблицы для определения широты по высоте Полярной звезды, для определения азимута Полярной, таблицы для исправления высот светил, таблицы для решения параллактического треугольника ТВА-52 и некоторые другие таблицы.
С помощью МАЕ решаются следующие астрономические задачи:
— расчёт часовых углов и склонений светил;
— расчёт времени кульминации, восхода или захода Солнца и Луны;
— расчёт времени начала и конца сумерек;
— определение возраста, фазы и параллакса Луны;
— определение поправки компаса по Полярной звезде;
— определение широты по высоте Полярной;
— исправление высот светил и приведение их к одному зениту.
Основной задачей, решаемой с помощью МАЕ, является определение
часовых углов и склонений светил. Для Солнца, Луны и планет задача решается в стандартной схеме в следующем порядке:
(показать на схеме.)
— 1.)расчёт по Тс приближенного Тгр.и гринвичской даты;
— расчёт точного Тгр. по хронометру;
— выборка часового угла и склонения на целый час (tT и δт),
— выборка поправок к часовому углу и склонению за минуты и секун
ды (Δt 1, Δ 2t, Δ S);

— расчёт гринвичского и местного часового угла и склонения (tгр.,, tM, δ);
— перевод полученного обыкновенного часового угла в практический.
2.) Для звезд схема получения часового угла и склонения несколько иная:
— расчёт по Тс приближённого Тгр. и гринвичской даты;
— расчёт точного Тгр. по хронометру;
— выборка звёздного времени на целый час (S Т );
— выборка поправки к звёздному времени за минуты и секунды (Δ S);
— расчёт гринвичского и местного звёздного времени (S гр ,SM);
— выборка звёздного дополнения и склонения (Т, δ );
— расчёт местного часового угла (tM );
— перевод полученного обыкновенного часового угла в практический.
Морской астрономический ежегодник предваряется описанием всех
таблиц, в котором приведены примеры решения различных задач.
Рассмотрим пример решения основной задачи — расчёта часового угла и склонения светила.
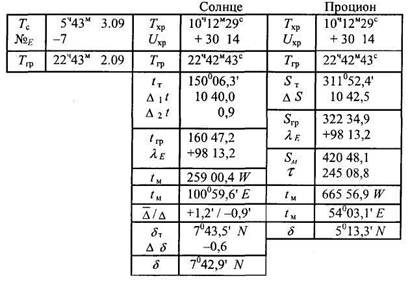
Пример 2.1. Дано: 3.09.02 г.; ТС=5 Ч 43 М ; λ= 98° 13,2′ Е; Тхр=10 ч 12 м 29 с ;
поправка хронометра Uхр= +30 м 14 с . Определить часовой угол и склонение Солнца и звезды Процион.
Решение. Решение производим в вышеизложенной последовательности в стандартных схемах. Добавим только, что для Солнца одновременно с tT и δт из ежедневных таблиц выбираются квазиразность (ˉΔ) и разность (Δ) , записываются в соответствующую строчку и затем по ним из основных интерполяционных таблиц (прил. 2) выбираются Δ2t и Δδ. Все выборки и вычисления записываем в стандартные схемы.
Звёздное дополнение и склонение Порциона под № (55) из списка звезд по алфавиту стр.320, выбираем из крайней правой колонки ежедневных таблиц, где приводятся видимые места 67 наиболее ярких звезд. Кроме того, эти же значения для всех 160 навигационных звезд даны в таблице «Видимых мест звёзд» в МАЕ.стр.270.
Результаты всех выборок и вычислений записываем в стандартные схемы. Часовые углы и склонения Луны и планет рассчитываются по той же стандартной схеме, что и Солнце. Отличие для Луны в том, что квазиразность и разность дается не на трое суток, как у Солнца и планет, а на каждый час.
 |
 |
 |
 |
 |
Рассмотрим пример решения задачи на расчет времени восхода или захода Солнца.
Пример 2.2. Рассчитать судовое время захода Солнца 2 сентября 2002г. в точке с координатами φ= 46°30′ N, λ= 30°46′ Е.
Решение. Из МАЕ (см. прил. 2 к учебнику) выбираем для ближайшей меньшей широты 45° N время захода Солнца 18 Ч 36 М . Это значение дано на 2.09. Если бы дата не совпадала (1.09 или 3.09) надо было бы выполнить интерполяцию в уме с помощью соответствующих значений на предыдущем или последующем развороте. Выбранное значение должно быть исправлено поправками за широту Δφи за долготуΔλ, которые вычисляются на калькуляторе линейной интерполяцией. Разность между заданной широтой и выбранной табличной (45°) составляет 1°30′. Из МАЕ видно, что при увеличении широты на 5° время захода изменяется на +7 М . Составляя пропорцию, находим, что при увеличении широты на 1°30′, момент изменится на +2 М . Таким образом, Δ Т φ=+2 м .
Поправка за долготу вычисляется по формуле:
где Δ — суточная разность с предыдущими сутками для восточных долгот и с последующими — для западных. В нашем случае Δ = +2 м и Δ Тλ=0. Все вычисления выполняются в следующей стандартной схеме.(18 ч 36 м 2.9.02. -18 ч 41 м 30.8.02.)
Поправки за широту и долготу можно также вычислить с помощью специальных интерполяционных таблиц, которые помещены в МАЕ.
Аналогично рассмотренному примеру вычисляется момент восхода Солнца, а также восхода или захода Луны, начала или конца сумерек. При вычислении сумерек поправка ΔТ λ не учитывается.
THE NAUTICAL ALMANAC
Этот альманах выпускается совместно Гринвичской обсерваторией в Англии и Морской обсерваторией США. В нем, как и в МАЕ, содержатся эфемериды Солнца, Луны, планет и звёзд, а также моменты восхода, захода Солнца и Луны, начала и конца сумерек, кульминации Солнца и Луны и некоторые другие данные.
На развороте альманаха приводятся эфемериды Солнца, Луны и планет
на трое суток. В ежедневных таблицах приводятся также звёздные дополнения и склонения 57 наиболее ярких звёзд. Видимые места 173 звёзд, включая упомянутые 57, на каждый месяц приведены на стр. 268-273.
Таблица широты по высоте Полярной звезды составлена таким образом, что на одной странице по аргументу SM выбираются сразу три поправки, причём все они положительные, но из широты нужно вычесть 1°.
В альманахе, как и в МАЕ, имеются таблицы для исправления высот светил, измеренных секстаном.
Отличительной особенностью является наличие таблиц для решения параллактического треугольника, которые относятся к, так называемым, искусственным таблицам. Подробнее об этих таблицах будет рассказано в разделе 2.3.
На стр. 277-283 приведены алгоритмы и примеры использования микрокалькулятора для интерполяции часовых углов и склонений, выбранных из ежедневных таблиц, решения параллактического треугольника, расчета наклонения горизонта, рефракции, параллакса при исправлении высот, расчета обсервованных координат при избыточных линиях положения.
Источник