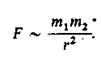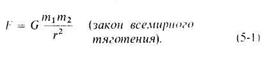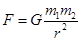Задание 67
Физика А.В. Перышкин
1.Определите центростремительное ускорение Луны при её обращении вокруг Земли. Необходимые для решения задачи данные найдите самостоятельно.
2. Используя дополнительную литературу и ресурсы Интернета, подготовьте доклад на тему «Планеты-карлики в Солнечной системе».
Карликовые планеты Солнечной системы — сравнительно новое понятие в классификации планет. Введено в 2006 году, после открытия Эриды.
По первоначальным данным, оказалось, что Эрида больше Плутона. В печати появились сообщения об открытии десятой планеты Солнечной системы. Потом последовали то опровержения, то подтверждения этого. Возникла неопределённость: что же всё-таки открыли — астероид или планету? Вдобавок, Плутон имеет всё-же довольно небольшой размер и ранее иногда возникали вопросы — считать его планетой или нет. Понятие «малая планета» тоже не подходило — к ним относятся и небольшие тела вроде Эроса и более внушительные, такие как Церера.
Поэтому было решено ввести новое понятие — карликовая планета Солнечной системы. Поскольку пока неясно, будет ли оно применяться к другим звёздным системам.
Для того, чтобы считаться карликовой планетой, небесное тело должно отвечать следующим условиям:
1) обращаться по собственной орбите вокруг Солнца, то есть тело не должно быть спутником планеты;
2) масса и создаваемая ею сила гравитации должны быть достаточны для поддержания гидростатического равновесия и иметь форму близкую к округлой;
3) в то же время, масса и гравитация недостаточны для доминирования на своей орбите и расчистки прилегающего пространства от других объектов.
В итоге, без вины виноватый Плутон больше не является планетой — его «разжаловали» в карликовые планеты Солнечной системы.
Стоит отметить, что эти требования всё-же страдают неопределённостью.
Например, если вдруг окажется, что Меркурий не смог до конца очистить свою орбиту и рядом с ним существует какой-то маленький астероид, не открытый пока из-за трудности наблюдений вблизи Солнца, то возникнет вопрос о переводе Меркурия в группу карликовых планет. (вероятность этого близка к нулю — приведено просто как пример).
Или напротив — объект больше Меркурия и по размерам, и по массе, имеющий округлую форму, но находящийся крайне далеко от Солнца не успел пока до конца расчистить свою орбиту вследствие крайне большого периода обращения вокруг Солнца. В пределы его орбиты мог «недавно» залететь астероид и остаться на этой новой орбите — из-за большого периода обращения, у планеты-хозяйки до него просто пока «не дошли руки». И тогда полноценная планета будет считаться карликовой!
Опять же, состав астероидов может быть самый разный, поэтому условия для гидростатического равновесия могут сильно различаться. Поэтому масса и размеры тоже могут колебаться в широких пределах. Тогда ледяная менее округлая громадина будет малой планетой, а гораздо меньшая по размеру, но более тяжёлая скала из горных пород получит более высокий статус карликовой планеты.
Поэтому многие астрономы до сих пор остаются несогласны с новой классификацией.
Сейчас к карликовым планетам Солнечной системы относят пять небесных тел:
Плутон, Хаумеа, Макемаке, Эрида и Церера.
Кроме них существуют ещё довольно много кандидатов на статус карликовой планеты Солнечной системы.
Во-первых, это три малых планеты из Главного пояса астероидов: Веста, Гигея и Паллада. Пока степень их гидростатического равновесия недостаточно известна. Недостающие данные о Весте должны были быть получены в 2011 году при исследовании Весты космическим аппаратом АМС Dawn (NASA), который вышел на её орбиту 16 июля 2011 года. На снимках видно, что форма этой карликовой планеты действительно близка к шарообразной, но об изменении статуса Весты пока не слышно.
Во-вторых, это уже известные объекты Рассеянного диска и пояса Койпера: Седна, Квавар, Варуна, Орк и другие. Вследствие их удалённости, пока нет точных данных об их массе и степени округлости.
Источник
Пример 1. Чему равно ускорение Луны и каково отношение этого ускорения к ускорению свободного падения на поверхности Земли?
Чему равно ускорение Луны и каково отношение этого ускорения к ускорению свободного падения на поверхности Земли?
Решение: Используя формулу для центростремительного ускорения, находим, что ускорение Луны 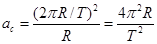
Вблизи поверхности Земли ускорение равно g = 9,8 м/с 2 .
Таким образом, отношение а/g = 1/3590 = (1/60) 2 .
Ньютон выполнил простые вычисления, близкие к описанным в примере 1, и обнаружил, что сила тяготения, действующая со стороны Земли на яблоко, удаленное к Луне, уменьшится в 3600 = (60) 2 раз, что соответствует отношению квадратов расстояний.
Отсюда Ньютон заключил, что сила тяготения между двумя телами должна убывать обратно пропорционально квадрату расстояния между ними.
Он предложил универсальный закон гравитационного притяжения между любыми двумя телами:
Для обозначения коэффициента пропорциональности используется прописная буква G. Таким образом,
Пример 2.
Предположив, что средняя плотность Земли равна ρ = 5 • 10 3 кг/м 3 , Ньютон нашел численное значение G. (Его догадка с точностью 10% совпала с истинным значением.) Получите выражение для G через ρ , rз и g.
Решение: Применим формулу (5-1)
к силе, действующей между Землей и яблоком.
Обозначим массу Земли Мз,
а массу яблока т.
Полагая r равным расстоянию rз между центром Земли и яблоком, имеем
В соответствии со вторым законом Ньютона эта сила должна равняться та, причем в нашем случае а = g. Таким образом,
Учитывая, что Mз равна произведению плотности на объем, т. е.
Подставляя сюда Rз = 6,37-10 6 м и ρ = 5 х 10 3 кг/м 3 , имеем
G = 7,35- 10 -11 Н -м 2 •кг -2 ,
что всего лишь на 10% превышает принятое значение
G = 6,67. 10 -11 Н -м 2 •кг -2
Сравнивая ускорение свободного падения на Луне с величиной этого ускорения на поверхности Земли, Ньютон предположил, что Земля ведет себя так, как если бы вся ее масса была сконцентрирована в центре. Ньютон догадался, что такое поведение справедливо в случае сил, изменяющихся обратно пропорционально квадрату расстояния. Однако ему удалось получить строгое доказательство лишь 20 лет спустя.
«Взвешивание –Земли»
Тяготение действует на огромных расстояниях.
Но закон Ньютона утверждает, что взаимно притягиваются все предметы.
А правда ли, что любые два предмета, притягивают друг друга?
Можем ли мы сами поставить такой опыт, а не гадать, глядя на небо, притягиваются ли планеты?
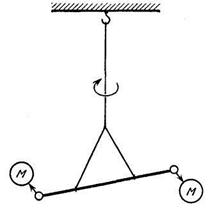
Такой прямой опыт сделал Кавендиш (1731 —1810) при помощи прибора, который показан на рис. 11. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара, как показано на рисунке. Притяжение шаров слегка перекрутит нить — слегка, потому что силы притяжения между обычными предметами очень слабы. Силу притяжения между двумя шарами можно измерить. Кавендиш назвал свой опыт «взвешиванием Земли».
Педантичный и осторожный преподаватель наших дней не позволит студентам так выразиться; нам пришлось бы сказать «измерение массы Земли». При помощи такого прибора Кавендишу удалось непосредственно измерить силу, расстояние и величину обеих масс и, таким образом, определить постоянную тяготения G.
Вы скажете: «Взвешивание Земли представляет собой почти такую же задачу. Мы знаем силу притяжения, знаем массу объекта, который притягивается, и знаем, насколько он удален, но мы не знаем ни массы Земли, ни постоянной тяготения, а только их произведение».
Измерив постоянную и зная, как Земля притягивает предметы, мы сможем вычислить ее массу.
Этот опыт впервые позволил косвенно определить, насколько тяжел, массивен шар, на котором мы живем. Результат его невольно вызывает удивление, и именно поэтому Кавендиш назвал свой опыт «взвешиванием Земли», а не «определением постоянной уравнения тяготения».
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Определение центростремительного ускорения луны при ее обращении вокруг земли
Рассмотрите таблицу, содержащую некоторые характеристики планет Солнечной системы. Размеры и параметры орбит даны в сравнении с планетой Земля.
| Имя | Диаметр | Масса | Орбитальный (земных суток) | ||
|---|---|---|---|---|---|
| Нептун | 3,9 | 17,2 | 30,1 | 165 | 0,67 |
| Уран | 4 | 14,6 | 19,2 | 84 | 0,72 |
| Сатурн | 9,5 | 95,2 | 9,5 | 29,5 | 0,43 |
| Юпитер | 11,2 | 318 | 5,2 | 11,9 | 0,41 |
| Марс | 0,53 | 0,11 | 1,5 | 1,9 | 1 |
| Земля | 1 | 1 | 1 | 1 | 1 |
| Венера | 0,95 | 0,82 | 0,72 | 0,62 | 243 |
| Меркурий | 0,38 | 0,06 | 0,39 | 0,24 | 58,6 |
Выберите два утверждения, которые соответствуют характеристикам планет.
1) Средняя плотность Венеры меньше средней плотности Земли.
2) Центростремительное ускорение Юпитера при его вращении вокруг Солнца больше центростремительного ускорения Марса.
3) Первая космическая скорость для Нептуна меньше, чем для Урана.
4) Ускорение свободного падения на Меркурии составляет примерно 4 м/с 2 .
5) Сила притяжения Сатурна к Солнцу больше, чем у Юпитера.
1) Средняя плотность планеты Отношение средней плотности Венеры к средней плотности Земли
меньше единицы. Значит, средняя плотность Венеры меньше средней плотности Земли.
Утверждение 1 верно.
2) Центростремительное ускорение планеты Юпитер расположен дальше от Солнца, чем Марс, поэтому центростремительное ускорение Юпитера при его вращении вокруг Солнца меньше центростремительного ускорения Марса.
Утверждение 2 неверно.
3) Первая космическая скорость Масса Нептуна больше массы Урана, а радиус Нептуна меньше радиуса Урана, значит, первая космическая скорость для Нептуна больше, чем для Урана.
Утверждение 3 неверно.
4) Ускорение свободного падения на планете Ускорение свободного падения на Меркурии по отношению к земному
И, значит,
Утверждение 4 верно.
5) Сила притяжения планеты к Солнцу Масса Сатурна меньше массы Юпитера и Сатурн расположен дальше от Солнца, чем Юпитер, поэтому сила притяжения Сатурна к Солнцу меньше, чем у Юпитера.
Источник
Определите центростремительное ускорение Луны, приняв её орбиту за окружность вокруг Земли радиусом 385 000 км и период обращения 27, 3 суток?
Физика | 5 — 9 классы
Определите центростремительное ускорение Луны, приняв её орбиту за окружность вокруг Земли радиусом 385 000 км и период обращения 27, 3 суток.
Радиус R = 385 000 км = 385 000 * 1000 = 385 000 000 м
длина орбиты L = 2pi * R
период обращения Т = 27, 3 суток = 27, 3 * 24 * 60 * 60 = 2358720 c
скорость движения по орбите v = L / T
центростремительное ускорение a = v ^ 2 / R = (L / T) ^ 2 / R = (2pi * R / T) ^ 2 / R = (2pi / T) ^ 2 / R ^ 3
a = (2pi / 2358720 ) ^ 2 / 385 000 000 ^ 3 = 1.
2434 * 10 ^ — 37 м / с2
Ответцентростремительное ускорение Луны1.
2434 * 10 ^ — 37 м / с2.
Луна движется почти равномерно по окружности радиусом 384000 км, совершая один оборот вокруг Земли за 27?
Луна движется почти равномерно по окружности радиусом 384000 км, совершая один оборот вокруг Земли за 27.
Вычислите центростремительное ускорение Луны.
Определите центростремительное ускорение Земли при её движении вокруг Солнца?
Определите центростремительное ускорение Земли при её движении вокруг Солнца.
Считайте орбиту Земли окружностью радиусом 1, 5 * 10 ^ 8 км.
Определите центростремительное ускорение земли при её движении вокруг Солнца?
Определите центростремительное ускорение земли при её движении вокруг Солнца.
Считайте орбиту Земли окружностью радиусом 1, 5х10 ^ 8.
Тело движется равномерно по окружности радиусом 1 м?
Тело движется равномерно по окружности радиусом 1 м.
Определите период обращения по окружности, если величина центростремительного ускорения составляет 4м / (сек в квадрате).
Период обращения материальной точки по окружности составляет 0, 2 с?
Период обращения материальной точки по окружности составляет 0, 2 с.
Центростремительное ускорение точки при этом равно 24 м / с ^ 2.
Определите радиус окружности.
1. Вычислите массу земли если известны ее радиус R = 6370км и ускорение свободного падения на ее поверхности g = 9, 81м / с в квадрате?
1. Вычислите массу земли если известны ее радиус R = 6370км и ускорение свободного падения на ее поверхности g = 9, 81м / с в квадрате?
2. Определите массу солнца если известны скорость вращения земли вокруг него v = 30км / с и радиус земной орбиты r = 1, 5 * 10 в 11 степени метров?
3. Период обращения луны вокруг земли равен T = 27 суток, определите радиус орбиты по которой движется луна?
Период обращения земли вокруг солнца равен 1 году( 365?
Период обращения земли вокруг солнца равен 1 году( 365.
25 суток) , радиус орбиты Земли 150 млн км.
Опрделите скорость движения земли вокруг солнца.
7. Луна движется вокруг Земли с периодом 27, 3 суток по круговой орбите?
7. Луна движется вокруг Земли с периодом 27, 3 суток по круговой орбите.
Радиус Земли равен 6400 км, а ускорение свободного падения на поверхности Земли 9, 8 м / с ^ <2>.
Определить по этим данным радиус орбиты Луны.
Луна движется почти равномерно по окружности радиусом 384 000 км, совершая один оборот вокруг Земли за 27, 3 суток?
Луна движется почти равномерно по окружности радиусом 384 000 км, совершая один оборот вокруг Земли за 27, 3 суток.
Вычислите скорость и центростремительное ускорение Луны.
4. Определите частоту вращения, центростремительное ускорение и линейную скорость вращения точек Луны вокруг своей оси у экватора?
4. Определите частоту вращения, центростремительное ускорение и линейную скорость вращения точек Луны вокруг своей оси у экватора.
Радиус Луны 1600 км, а период обращения вокруг оси 27, 3 суток.
На этой странице сайта вы найдете ответы на вопрос Определите центростремительное ускорение Луны, приняв её орбиту за окружность вокруг Земли радиусом 385 000 км и период обращения 27, 3 суток?, относящийся к категории Физика. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
30г = 0, 03кг удельная теплота плавления = количество теплоты разделить на массу2010 : 0, 03 = 67000.
2010 Дж / 0, 03 кг = 67000 Дж / кг.
Закон сохранения импульса : если сумма внешних сил, действующих на тела системы, равна нулю, то импульс системы сохраняется.
Закон сохранения импульса а) Если система замкнута, т. Е. внешние силы отсутствуют, или если их сумма равна нулю, то импульс системы сохраняется : Σp = const. Б) Если внешние силы перпендикулярны некоторой осиx, то проекция импульса системы на это..
108км / ч×22, 5ч = 2430км 25000м : 5м / с = 5000с = 83ч 20мин 2мин×18м / ч = 2мин×18см / м = 36см.
1) 2 ч * 100 км / ч = 200 км S₂ 2) 200 км : 80 км / ч = 2, 5 ч t₁ 3) 200 км + 200 км = 400 км Sобщ 4) 2 ч + 2, 5 ч = 4, 5 ч tобщ 5) 400 км : 4, 5 ч ≈ 88, 9 км / ч Ответ : ≈88, 9 км / ч.
\ 20 ненужных символов /.
P = 10 * 800 * 10 / 0. 25 = 320000н.
К жидкому. Это мельчайшие капельки воды, взвешенные в воздухе. А при низких отрицательных температурах это могут быть кристаллики льда.
P = 101300 Па g = 9. 8 Н / кг po = 1261 кг / м3 (плотность глицерина) h = ? = = = p = po * g * h h = p / (po * g) = 101300 / (1261 * 9. 8) = 8. 2 м = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =.
Источник