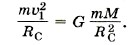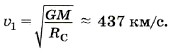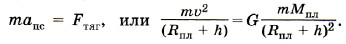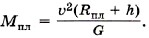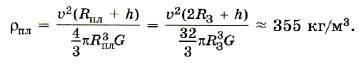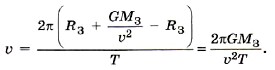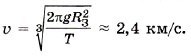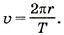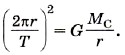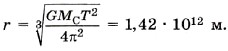Некоторая планета массы м движется по окружности вокруг солнца со скоростью

Некоторая планета массы м движется по окружности вокруг солнца со скоростью

1.237 Некоторая планета движется по окружности вокруг Солнца со скоростью v = 34,9 км/с (относительно гелиоцентрической системы отсчета). Найти период обращения этой планеты вокруг Солнца.
→ Перейти к решению

1.238 Период обращения Юпитера вокруг Солнца в 12 раз больше соответствующего периода для Земли. Считая орбиты планет круговыми, найти: а) во сколько раз расстояние от Юпитера до Солнца превышает расстояние от Земли до Солнца; б) скорость и ускорение Юпитера в гелиоцентрической системе отсчета.
→ Перейти к решению

1.239 Некоторая планета движется вокруг Солнца по эллипсу так, что минимальное расстояние между ней и Солнцем равно r1, а максимальное r2. Найти с помощью (1.46) период обращения ее вокруг Солнца.
→ Перейти к решению

1.240 Два спутника движутся вокруг Земли по касающимся траекториям. Один спутник движется по окружности радиуса r, другой — по эллипсу с периодом обращения, в h раз большим, чем у первого спутника. Найти с помощью (1.46) максимальное расстояние между вторым спутником и центром Земли.
→ Перейти к решению

1.241 Небольшое тело начинает падать на Солнце с расстояния, равного радиусу земной орбиты. Найти с помощью (1.46) продолжительность падения.
→ Перейти к решению

1.242 Спутник Луны, двигавшийся по круговой орбите радиуса r, после кратковременного торможения стал двигаться по эллиптической орбите, касающейся поверхности Луны. Найти с помощью (1.46) время падения спутника на Луну.
→ Перейти к решению

1.243 Представим себе, что мы создали модель Солнечной системы, в h раз меньшую натуральной величины, но из материалов той же самой средней плотности, что у Солнца и планет. Как изменятся при этом периоды обращения моделей планет по своим орбитам?
→ Перейти к решению

1.244 Двойная звезда — это система из двух звезд, движущихся вокруг ее центра масс. Известны расстояние l между компонентами двойной звезды и период T ее вращения. Считая, что l не меняется, найти массу системы.
→ Перейти к решению

1.245 Планета массы m движется по эллипсу вокруг Солнца так, что наименьшее и наибольшее расстояния ее от Солнца равны соответственно r1 и r2. Найти момент импульса М этой планеты относительно центра Солнца.
→ Перейти к решению

1.246 Доказать с помощью законов сохранения, что полная механическая энергия Е планеты массы m, движущейся вокруг Солнца по эллипсу, зависит только от его большой полуоси а. Найти зависимость Е(а).
→ Перейти к решению

1.247 Планета A движется по эллиптической орбите вокруг Солнца. В момент, когда она находилась на расстоянии r0 от Солнца, ее скорость равнялась v0 и угол между радиусом-вектором r0 и вектором скорости v0 составлял а. Найти наибольшее и наименьшее расстояния, на которые удаляется от Солнца эта планета при своем движении.
→ Перейти к решению

1.248 Космическое тело A движется к Солнцу С, имея вдали от него скорость v0 и прицельный параметр l — плечо вектора v0 относительно центра Солнца (рис. ). Найти наименьшее расстояние, на которое это тело приблизится к Солнцу.
→ Перейти к решению

1.249 Частица массы m находится вне однородного шара массы М на расстоянии r от его центра. Найти: а) потенциальную энергию гравитационного взаимодействия частицы и шара; б) силу, с которой шар действует на частицу.
→ Перейти к решению

1.250 Доказать, что сила тяготения, действующая на частицу A внутри однородного сферического слоя вещества, равна нулю.
→ Перейти к решению

1.251 Имеется однородный шар массы М и радиуса R. Найти напряженность G и потенциал ф гравитационного поля этого шара как функции расстояния r от его центра (при r R). Изобразить примерные графики зависимостей G® и ф®.
→ Перейти к решению

1.252 Внутри однородного шара плотности р имеется сферическая полость, центр которой находится на расстоянии 1 от центра шара. Найти напряженность G поля тяготения внутри полости.
→ Перейти к решению

1.253 Однородный шар имеет массу М и радиус R. Найти давление р внутри шара, обусловленное гравитационным сжатием, как функцию расстояния r от его центра. Оценить р в центре Земли, считая, что Земля является однородным шаром.
→ Перейти к решению

1.254 Найти собственную потенциальную энергию гравитационного взаимодействия вещества, образующего: а) тонкий однородный сферический слой массы m и радиуса R; б) однородный шар массы m и радиуса R (воспользоваться ответом к задаче 1.251).
→ Перейти к решению

1.255 Вычислить отношение следующих ускорений: ускорения a1, вызываемого силой тяготения на поверхности Земли; ускорения a2, обусловленного центробежной силой инерции на экваторе Земли; ускорения a3, сообщаемого телам на Земле Солнцем.
→ Перейти к решению

1.256 На какой высоте над полюсом Земли ускорение свободного падения убывает на h = 1,0%? в n = 2,0 раза?
→ Перейти к решению

1.257 Телу сообщили на полюсе Земли скорость v0, направленную вертикально вверх. Зная радиус Земли и ускорение свободного падения на ее поверхности, найти высоту, на которую поднимается тело.
→ Перейти к решению

1.258 Найти период обращения спутника, движущегося вокруг некоторой планеты вблизи ее поверхности, если средняя плотность планеты р = 3,3 г/см3.
→ Перейти к решению

1.259 Спутник вывели на круговую орбиту со скоростью v над полюсом Земли. Найти расстояние от спутника до поверхности Земли.
→ Перейти к решению

1.260 Спутник Земли массы m движется по круговой орбите, радиус которой вдвое больше радиуса Земли. Какой дополнительный импульс и в каком направлении следует кратковременно сообщить спутнику, чтобы плоскость его орбиты повернулась на угол а без изменения радиуса орбиты?
→ Перейти к решению

1.261 Вычислить радиус круговой орбиты стационарного спутника Земли, который остается неподвижным относительно ее поверхности. Какова его скорость в инерциальной системе отсчета, связанной в данный момент с центром Земли?
→ Перейти к решению

1.262 Система, которая состоит из двух одинаковых спутников, соединенных тонким тросом длины l = 150 м, движется по круговой орбите вокруг Земли. Масса каждого спутника m = 1000 кг, масса троса пренебрежимо мала, расстояние от центра Земли до этой системы составляет h = 1,2 радиуса Земли. Найти силу натяжения троса в момент, когда трос направлен по радиусу Земли.
→ Перейти к решению

1.263 Найти массу Земли, если спутник, движущийся в ее экваториальной плоскости с запада на восток по круговой орбите радиуса R = 2,00*10^4 км, появляется над некоторым пунктом на экваторе через каждые т = 11,6 ч.
→ Перейти к решению

1.264 Спутник движется в экваториальной плоскости Земли с востока на запад по круговой орбите радиуса R = 1,00*10^4 км. Найти относительно поверхности Земли: а) скорость спутника; б) его ускорение.
→ Перейти к решению

1.265 Какую скорость необходимо сообщить телу в горизонтальном направлении вблизи поверхности Земли у ее полюса, чтобы вывести его на эллиптическую орбиту с большой полуосью а?
→ Перейти к решению

1.266 Искусственный спутник Луны движется по круговой орбите, радиус которой в h раз больше радиуса Луны. Считая, что небольшая сила сопротивления, испытываемая спутником со стороны космической пыли, зависит от его скорости как F = av2, где a — постоянная, найти время движения спутника до падения на поверхность Луны.
→ Перейти к решению

1.267 Вычислить первую и вторую космические скорости для запусков с Луны. Сравнить с соответствующими скоростями для Земли.
→ Перейти к решению

1.268 Космический корабль подлетает к Луне по параболической траектории, почти касающейся ее поверхности. В момент максимального сближения с Луной на короткое время был включен тормозной двигатель, и корабль перешел на круговую орбиту. Найти приращение модуля скорости корабля при торможении.
→ Перейти к решению

1.269 Космический корабль вывели на круговую орбиту вблизи поверхности Земли. Какую дополнительную скорость в направлении его движения необходимо кратковременно сообщить кораблю, чтобы он смог преодолеть земное тяготение?
→ Перейти к решению

1.270 Космический корабль движется вокруг Земли по круговой орбите, радиус которой в h = 2,5 раза больше радиуса Земли. Какую дополнительную скорость надо кратковременно сообщить кораблю в направлении от центра Земли по ее радиусу, чтобы он смог покинуть поле тяготения Земли?
→ Перейти к решению

1.271 Найти приближенно третью космическую скорость v3 — наименьшую скорость, которую необходимо сообщить телу относительно поверхности Земли, чтобы оно могло покинуть Солнечную систему. Вращением Земли вокруг ее оси пренебречь.
→ Перейти к решению

Источник

§ 32. Примеры решения задач по теме «Первая космическая скорость

Для решения задач требуется знать закон всемирного тяготения, закон Ньютона, а также связь линейной скорости тел с периодом их обращения вокруг планет. Обратите внимание на то, что радиус траектории спутника всегда отсчитывается от центра планеты.

Задача 1. Вычислите первую космическую скорость для Солнца. Масса Солнца 2 • 10 30 кг, диаметр Солнца 1,4 • 10 9 м.

Р е ш е н и е. Спутник движется вокруг Солнца под действием единственной силы — силы тяготения. Согласно второму закону Ньютона запишем:

Из этого уравнения определим первую космическую скорость, т. е. минимальную скорость, с которой надо запустить тело с поверхности Солнца, чтобы оно стало его спутником:

Задача 2. Вокруг планеты на расстоянии 200 км от её поверхности со скоростью 4 км/с движется спутник. Определите плотность планеты, если её радиус равен двум радиусам Земли (R_пл = 2R₃).

Р е ш е н и е. Планеты имеют форму шара, объём которого можно вычислить по формуле тогда плотность планеты

где М_пл — масса планеты, R_пл — её радиус.

Спутник движется вокруг планеты по круговой орбите. На него действует сила тяготения F_тяг, которая определяет центростремительное ускорение.

Согласно второму закону Ньютона

Из последнего уравнения находим массу планеты:

Подставив это выражение в формулу (1), имеем

Задача 3. При какой скорости спутника период его обращения вокруг Земли равен двум суткам?

Р е ш е н и е. Скорость спутника

где h — высота спутника над поверхностью Земли.

Для определения скорости необходимо знать высоту h.

Спутник движется по круговой орбите, при этом сила тяготения является центростремительной силой. Согласно второму закону Ньютона для спутника запишем:

где m — масса спутника.

Из уравнения (2) находим высоту Подставим выражение для h в формулу (1) и из полученного уравнения определим искомую скорость:

Для упрощения расчётов поместим спутник на полюс, где сила тяжести равна силе тяготения. Тогда 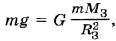отсюда GM₃ = gR 2 ₃.

Подставив найденное выражение в формулу (3), определим скорость:

Задача 4. Определите среднее расстояние от Сатурна до Солнца, если период обращения Сатурна вокруг Солнца равен 29,5 лет. Масса Солнца равна 2 • 10 30 кг.

Р е ш е н и е. Считаем, что Сатурн движется вокруг Солнца по круговой орбите. Тогда согласно второму закону Ньютона запишем:

где m — масса Сатурна, r — расстояние от Сатурна до Солнца, М_с — масса Солнца.

Период обращения Сатурна 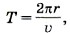отсюда

Подставив выражение для скорости υ в уравнение (4), получим

Из последнего уравнения определим искомое расстояние от Сатурна до Солнца:

Сравнив с табличными данными, убедимся в правильности найденного значения.

Задачи для самостоятельного решения

1. Определите длительность года на Венере. Среднее расстояние от Венеры до Солнца 1,08 • 10 8 км, а от Земли до Солнца 1,49 • 10 8 км.

2. Какой импульс силы подействовал на спутник массой 1 т, если спутник перешёл с орбиты радиусом R₃ + h на орбиту радиусом R₃ + 2h, где высота h равна 200 км?

3. Астероид вращается вокруг Солнца с периодом, равным 410 сут. Определите расстояние от астероида до Солнца.

Образцы заданий ЕГЭ

С1. Чему равен радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна 5,7 • 10 26 кг.

С2. Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн км, а от планеты Юпитер до Солнца — 778,3 млн км. Чему равно отношение υ_З/υ_Ю линейных скоростей этих двух планет при их движении вокруг Солнца, если считать их орбиты окружностями?

С3. Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн км, а до планеты Земля — 149,6 млн км. Чему приблизительно равна средняя линейная скорость планеты Уран при её движении вокруг Солнца, если известно, что средняя скорость движения Земли по орбите вокруг Солнца составляет 30 км/с?

С4. Средняя плотность некоторой планеты равна средней плотности планеты Земля, а радиус этой планеты в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на этой планете к первой космической скорости на Земле υ_п/υ₃.

Источник