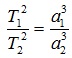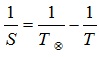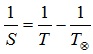Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
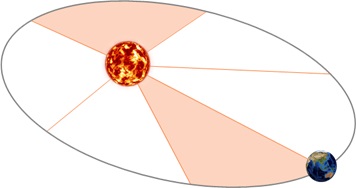
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
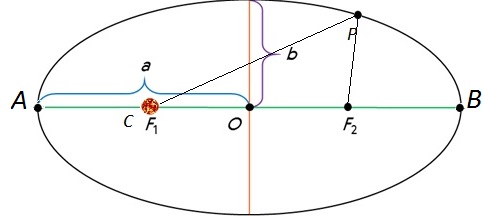
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
6. Выполните задание.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Все знают, что это невозможно. Но вот приходит невежда, которому это неизвестно — он-то и делает открытие.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»
Тема: Законы Кеплера. Определение масс небесных тел
Цель занятия: Освоить методику решения задач, используя законы движения планет.
Теоретические сведения
При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.
Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.
Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:
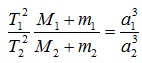
где М1 и М2 -массы каких-либо небесных тел, а m1 и m2 — соответственно массы их спутников.
Обобщённый третий закон Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:
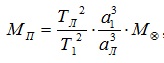
где Тл и α л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.
Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,
а) для внешней планеты формула имеет вид:
б) для внутренней планеты:
Выполнение работы
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.
Задание 7. Определить период обращения астероида Белоруссия если большая полуось его орбиты а=2,4 а.е.
Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?
Примеры решения задач 1-4
Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?
Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км
Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?
Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.
Источник
Найдите связь между периодом обращения планеты вокруг солнца
Цель работы: изучение движения тел под действием сил тяготения; проверка третьего закона Кеплера.
На смену геоцентрической системе мира, созданной в начале нашей эры Птолемеем, пришла гелиоцентрическая система, созданная Коперником. Несколько позднее немецкий астроном И. Кеплер на основе астрономических наблюдений установил законы движения планет вокруг Солнца.
Согласно 1-му закону Кеплера любая планета движется вокруг Солнца по замкнутой кривой, которая называется эллипсом (внешне похож на овал). Солнце находится в одном из фокусов этого эллипса. Эллипс имеет два фокуса: это две такие точки внутри кривой, сумма расстояний от которых до произвольной точки эллипса постоянна. Оказывается, что орбиты всех планет Солнечной системы лежат примерно в одной плоскости. Большинство планет движутся по орбитам-эллипсам, которые близки к окружностям. Лишь Марс и Плутон имеют сравнительно вытянутые орбиты.
Второй закон Кеплера устанавливает, что скорость планеты больше тогда, когда она в своем движении находится ближе к Солнцу (в так называемой точке перигелия) и меньше тогда, когда она находится на наибольшем расстоянии от Солнца (в точке афелия). Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и ее средним расстоянием от Солнца, он применяется ко всему коллективу планет Солнечной системы.
Законы Кеплера получили свое объяснение лишь после открытия законов тяготения. Физические объекты участвуют в гравитационном взаимодействии, т.е. они притягиваются друг к другу. Гравитационное взаимодействие обладает всеобщей универсальностью: ему подвержены все материальные объекты и даже физические поля. Закон всемирного тяготения был открыт И. Ньютоном. Он утверждает, что два неподвижных точечных тела взаимодействуют друг с другом с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними, т.е.
 , , | (1) |
где γ называют гравитационной постоянной. Этот закон справедлив и для взаимодействия однородных шаров, но в этом случае под r следует понимать расстояние между их центрами.

Отсюда получаем, что 


 . . | (2) |
Это и есть третий закон Кеплера, который можно сформулировать следующим образом: отношение куба расстояния от планеты до Солнца к квадрату периода ее обращения вокруг Солнца есть величина постоянная, одинаковая для всех планет Солнечной системы. В случае движения по эллипсу, когда расстояние от планеты до Солнца при движении изменяется, в законе фигурирует некоторое среднее расстояние, т.е. полусумма максимального и минимального расстояний от данной планеты до Солнца. Закон Кеплера справедлив для любой планетной системы, а также для системы спутников какой-либо конкретной планеты, например, для системы спутников Юпитера или Урана. В последнем случае под М в формуле (2) понимается масса соответственно Юпитера или Урана.
Источник
Найдите связь между периодом обращения планеты вокруг солнца
§ 11. К онфигурация планет. С инодический период
1. Конфигурация планет и условия их видимости
У словия видимости планет Подробные сведения о положении планет и условиях их видимости даются в «Школьном астрономическом календаре» на каждый учебный год. Эту информацию можно найти и в Интернете. меняются по-разному: если Меркурий и Венеру можно видеть только утром или вечером, то остальные — Марс, Юпитер и Сатурн — бывают видны также и ночью. По временам одна или несколько планет могут быть вовсе не видны, поскольку они располагаются на небе поблизости от Солнца. В этом случае говорят, что планета находится в соединении с Солнцем. Если же планета располагается на небе вблизи точки, диаметрально противоположной Солнцу, то она находится в противостоянии . В этом случае планета появляется над горизонтом в то время, когда Солнце заходит, а заходит она одновременно с восходом Солнца. Следовательно, всю ночь планета находится над горизонтом.
Соединение и противостояние, а также другие характерные расположения планеты относительно Солнца называются конфигурациями . Внутренние планеты (Меркурий и Венера), которые всегда находятся внутри земной орбиты, и внешние, которые движутся вне её (все остальные планеты), меняют свои конфигурации по-разному. Названия различных конфигураций внутренних и внешних планет, которые характеризуют расположение планеты относительно Солнца на небе, приведены в таблице и на рисунке 3.4.
Рис. 3.4. Конфигурации внутренней и внешней планеты
Источник
Астрономия. Решение задач. Тема: Законы Кеплера
Из опыта работы
Тема : Законы Кеплера
Звездный период обращения Юпитера вокруг Солнца составляет около 12 лет. Каково среднее расстояние Юпитера от Солнца?
Среднее расстояние планеты от Солнца равно большой полуоси эллиптической орбиты a. Из третьего закона Кеплера


для определения среднего расстояния планеты от Солнца в астрономических единицах по известному звездному (сидерическому) периоду обращения, выраженному в годах. Подставив численные значения окончательно найдем:

Ответ: около 5 а.е.
Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а=2,88 а. е., а эксцентриситете =0,24
а=2,88 а.е
е=0,24
_________________________
Радиус перигелия рассчитывается по формуле: r=(1-e)а, где: a — большая полуось; е — эксцентриситет орбиты.
Афелий орбиты рассчитывается по формуле r =(1+е)а, где a — большая полуось; е — эксцентриситет орбиты.
r=2.88(1 +0,24)=3.57 а.е
Ответ: 3.57 а.е
Период обращения малой планеты Шагал вокруг Солнца Т=5,6 года. Определите большую полуось ее орбиты.

а1=Т1 2
а1=3√5,6 2 =3.2 а.е
Ответ: 3.2 а.е
Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а=160 млн км, а эксцентриситет е=0,83.
а = 160 млн. км
е = 0,83
_________________________
r=?
r=(1-e)а
r=1,6*10 8 (1-0,83)=2,72*10 7 км
Ответ: 2,72*10 7 км
просмотров всего 64,042 , просмотров сегодня 48
Источник