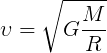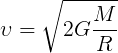Формулы и калькулятор космических скоростей
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.
Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Источник
Формулы и калькулятор космических скоростей
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.
Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Источник