Наибольшую полуденную высоту солнца
5. Эклиптика. Видимое движение Солнца и Луны
В данной местности каждая звезда кульминирует всегда на одной и той же высоте над горизонтом, потому что ее угловое расстояние от полюса мира и от небесного экватора остается неизменным. Солнце же и Луна меняют высоту, на которой они кульминируют. Отсюда можно сделать вывод, что их положение относительно звезд (склонение) изменяется. Мы знаем, что Земля движется вокруг Солнца, а Луна вокруг Земли. Проследим, как меняется вследствие этого положение обоих светил на небе.
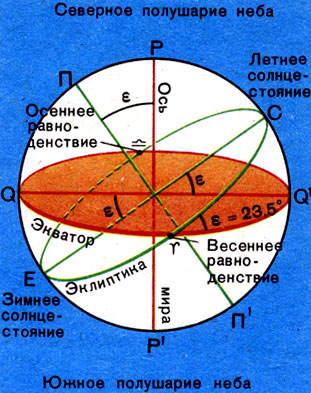
Если по точным часам замечать промежутки времени между верхними кульминациями звезд и Солнца, то можно убедиться, что промежутки между кульминациями звезд на четыре минуты короче, чем промежутки между кульминациями Солнца. Объясняется это тем, что за время одного оборота вокруг оси (сутки) Земля проходит примерно 1 /365 часть своего пути вокруг Солнца. Нам же кажется, что Солнце сдвигается на фоне звезд к востоку — в сторону, противоположную суточному вращению неба. Этот сдвиг составляет около 1°. Чтобы повернуться на такой угол, небесной сфере нужно еще 4 мин, на которые и «запаздывает» кульминация Солнца. Таким образом, в результате движения Земли по орбите Солнце за год описывает на небе относительно звезд большой круг, называемый эклиптикой (рис. 17).
Рис. 17. Эклиптика и небесный экватор
Так как Луна совершает один оборот настречу вращению неба за месяц и потому проходит за сутки не 1°, а примерно 13°, то ее кульминации запаздывают ежесуточно уже не на 4 мин, а на 50 мин.
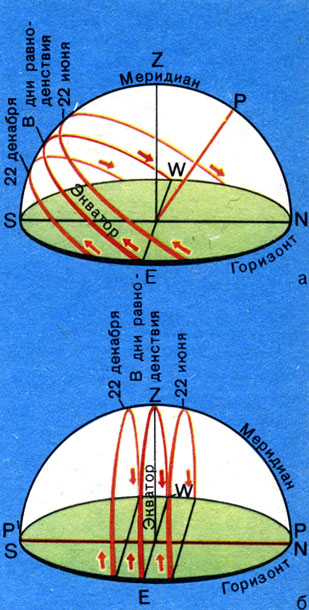
Определяя высоту Солнца в полдень, заметили, что дважды в году оно бывает на небесном экваторе, в так называемых равноденственных точках. Это происходит в дни весеннего и осеннего равноденствий (около 21 марта и около 23 сентября). Плоскость горизонта делит небесный экватор пополам (рис. 18). Поэтому в дни равноденствий пути Солнца над и под горизонтом равны, следовательно, равны продолжительности дня и ночи.
Рис. 18. Суточные пути Солнца над горизонтом в разные времена года при наблюдениях: а — в средних географических широтах; б — на экваторе Земли
Каково склонение Солнца в дни равноденствий?
Двигаясь по эклиптике, Солнце 22 июня отходит дальше всего от небесного экватора в сторону северного полюса мира (на 23°27′). В полдень для северного полушария Земли оно выше всего над горизонтом (на эту величину выше небесного экватора, см. рис. 17 и 18). День самый длинный, он называется днем летнего солнцестояния.
Большой круг эклиптики пересекает большой круг небесного кватора под углом 23°27′. На столько же Солнце бывает ниже кватора в день зимнего солнцестояния, 22 декабря (см. рис. 17 и 18). Таким образом, в этот день высота Солнца в верхней кульминации уменьшается по сравнению с 22 июня на 46°54′, и день самый короткий. (Из курса физической географии вы знаете, что различия в условиях освещения и нагревания Земли Солнцем определяют ее климатические пояса и смену времен года.)
Обожествление Солнца в древности породило мифы, описывающие периодически повторяющиеся события «рождения», «воскресения» «бога-Солнца» в течение года: умирание природы зимой, ее возрождение весной и т. п. Христианские праздники носят в себе следы культа Солнца.
Путь Солнца пролегает через 12 созвездий, называемых зодиакальными ( от греческого слова зоон — животное), а их совокупность называется поясом зодиака. В него входят следующие созвездия: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей. Каждое зодиакальное созвездие Солнце проходит около месяца. Точка весеннего равноденствия 
(одно из двух пересечений эклиптики с небесным экватором) находится в созвездии Рыб.
Понятно, что в полночь верхнюю кульминацию проходит зодиакальное созвездие, противоположное тому, в котором находится Солнце. Например, в марте Солнце проходит по созвездию Рыб, а в полночь кульминирует созвездие Девы.
Итак, мы убедились, что видимое движение Луны, которая обращается вокруг Земли, и Солнца, вокруг которого обращается Земля, обнаруживается и описывается одинаково. И на основе только этих наблюдений нельзя решить, движется ли Солнце вокруг Земли или Земля вокруг него.
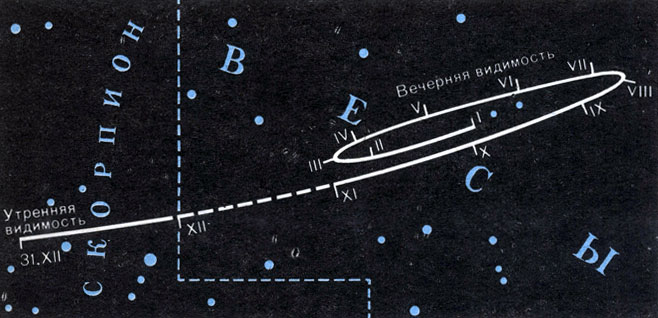
Планеты перемещаются на фоне звездного неба более сложным образом. Они движутся то в одну, то в другую сторону, иногда медленно выписывая петли (рис. 19). Это обусловлено сочетанием их истинного движения с движением Земли. На звездном небе планеты (в переводе с древнегреческого «блуждающие») не занимают постоянного места, так же как Луна и Солнце. Поэтому на карте звездного неба положение Солнца, Луны и планет можно указать лишь для определенного момента.
Рис. 19. Пример видимого пути планеты по небу за год
Пример решения задачи
Задача. Определите полуденную высоту Солнца в Архангельске и в Ашхабаде в дни летнего и зимнего солнцестояния.
Обратите внимание на то, как связана разность полуденных высот Солнца в дни солнцестояний (для каждого города) с различием его склонения в эти даты.
Сравните различие высоты Солнца в один и тот же день в этих двух городах с разностью их географических широт. Сделайте вывод.
Как, зная в день летнего солнцестояния высоту Солнца в полдень в одном из городов, можно вычислить его высоту в другом городе?
Упражнение 4
1. На какой географической широте Солнце в день летнего солнцестояния кульминирует в зените?
2. В какие дни года Солнце достигает зенита для наблюдателя, находящегося на земном экваторе?
3. Определите географическую широту пункта, в котором в день зимнего солнцестояния кульминация Солнца происходит в точке юга.
Задание 3
1. Найдите 12 зодиакальных созвездий на звездной карте. Пользуясь подвижной картой звездного неба, определите, какие из них будут видны над горизонтом в вечер наблюдения.
2. По «Школьному астрономическому календарю» найдите координаты планет в данное время и определите по карте, в каком созвездии они находятся. Найдите их вечером на небе.
Источник
ЗАВИСИМОСТЬ ВЫСОТЫ СОЛНЦА ОТ ГЕОГРАФИЧЕСКОЙ ШИРОТЫ
Поскольку широта местности не меняется, из изменений высоты Солнца следует, что меняется его склонение. Широту местности приближенно для данного населенного пункта можно определить по географической карте (для Ростова 47° 13″), тогда по измерениям высоты h можно найти, что летом максимальное удаление от небесного экватора составляет +23,5°, а в зимнее время равно -23,5°. Также можно установить, что на небесном экваторе Солнце находится 21 марта и 23 сентября (дни равноденствия), в эти дни склонение Солнца равно 0°.
Например, нужно определить максимальную и минимальную высоту подъёма Солнца над горизонтом для города Киева. Широта Киева: 50° 24″
H = 90° — 50,2° + 23,5° = 63,3° (в дни летнего солнцестояния);
H = 90° — 50,2° — 23,5° = 16,3° (в дни зимнего солнцестояния).
Bо время весеннего и осеннего равноденствий полуденная высота Солнца равна дополнению географической широты места до 90°, а во время зимнего и летнего солнцестояний она меньше или больше равноденственной на угол, равный наклонности эклиптики к экватору.
В дни равноденствий высота полуденного Солнца (φ0) над горизонтом для разных широт (φ1) определяется по формуле:
φ0 = 90° — φ1
Координаты Донецка: 48°00′32″ с. ш. 37°48′15″ в. д.
В г. Донецке 21 марта и 23 сентября в полдень Солнце находится на высоте:
φ0 = 90° — 48°= 42 °
Летом, когда Солнце находится над тропиком каждого полушария, высота его в полдень увеличивается на 23° 27′, т. е.
φ0 = 90° — φ1 + 23° 27′
φ0 = 90°- 48° +23° 27’= 65° 27′
В Донецке 21 июня высота Солнца равна 65°27′
Зимой, когда Солнце перемещается в противоположное полушарие, высота его соответственно уменьшается и достигает минимума в дни солнцестояния, когда ее следует уменьшить на 23°27′, т. е.
φ0 = 90° — φ1- 23° 27′
φ0 = 90°- 48° — 23° 27’= 18° 33′
В Донецке 22 декабря Солнце находится на высоте 18° 33′
Задача 31
Z — точка зенита * — Полярная звезда
угол, под которым видно Полярную звезду, к площади горизонта
угол между точкой зенита и Полярной звездой.
В дни равноденствий высота полуденного Солнца над горизонтом 
для разных широт 
определяется по формуле:
Так, например, в г. Киеве 
21 марта и 23 сентября в полдень Солнце находится на высоте:
Летом, когда Солнце находится над тропиком каждого полушария, высота его в полдень увеличивается на 23° 27′, т.е.
Таким образом, для г. Киева 21 июня высота Солнца равна 61°27′. Зимой, когда Солнце перемещается в противоположное полушарие, высота его соответственно уменьшается и достигает минимума в дни солнцестояния, когда ее следует уменьшить на 23°27′, т.е.
Так, для Киева 22 декабря Солнце находится на высоте 
Задача 33
С корабля 20 февраля была измерена высота Солнца над горизонтом. Она составила 50°. Солнце было на юге. На какой географической широте находится корабль, если в этот день Солнце, стояло в зените па широте 1105′ ю.ш.?
Ответ:
Корабль находился на 28°55′ с.ш.
Задача 32
Санкт-Петербург и Киев находятся почти на одном меридиане. 22 июня в полдень Солнце в Санкт-Петербурге возвышаетсянад горизонтом на 53°30, а в Киеве в этот момент- на 61,5°. Каково расстояние между городами в градуса и километрах?
Ответ:
Расстояние между Киевом и Санкт-Петербургом — 8°, а в километрах -890,4 км.
Задача 34
В Северном полушарии, там, где находятся туристы, Солнце в полдень стоит над горизонтом под углом 53030′. В этот же день полуденное Солнце находится в зените на 12°20′ с.ш. На каком градусе широты находятся туристы? 
Ответ:
Туристы находятся на 48°50′ с. ш.
— Высота Полярной ВСЕГДА равна широте места наблюдения (это для сев. полушария) = причём в любое время суток!
Источник
Видимое годовое движение Солнца, смена сезонов года и астрономические признаки тепловых поясов
В нашу эпоху эклиптика наклонена к небесному экватору под углом ε=23°27′ и поэтому склонение Солнца на протяжении года меняется в пределах ±23°27′. Наклон земной оси определяется углом между нею и перпендикуляром к плоскости земной орбиты (к оси эклиптики).
Если через Е0 обозначить количество тепла, получаемого единицей площади земной поверхности от Солнца, находящегося в зените, то при зенитном расстоянии Солнца ζ та же единица площади получает количество тепла
что позволяет сравнивать Е1 и Е2 при зенитных расстояниях Солнца z1 и z2.
Гражданские сумерки «длятся до погружения Солнца под горизонт на 7° (h = —7° и z = 97°). Если же даже в нижней кульминации высота Солнца hн≥—7° (zн≤97°), то гражданские сумерки длятся до восхода Солнца и называются белыми ночами.
Подставляя в формулу (8) hн=-7°, легко найти географическую широту мест, в которых наступают белые ночи при различных значениях склонения Солнца. Та же формула, при подстановке в нее hн = -18° дает границу темных ночей, при которых заревое освещение полностью исчезает. При hн=-0°,9 верхний край солнечного диска обычно касается горизонта, и тем самым определяется начало и окончание полярного дня. Начало и окончание полярной ночи обусловлено полуденной высотой Солнца: hв = — 0°,9 (или zв = 90°,9) *.
* Приведенные значения hн и hв учитывают величину радиуса солнечного диска (
0°,3) и среднюю рефракцию в горизонте
Длительность периода белых ночей, полярного дня и полярной ночи находится по календарным датам, в которые склонение Солнца имеет вычисленное или заданное значение, а сами даты устанавливаются по астрономическим календарям-ежегодникам.
При решении таких задач достаточно принимать значения географической широты и склонения Солнца с точностью до 0°,1.
Пример 1.На какой географической широте Солнце кульминирует в день летнего солнцестояния на высоте +72°50′ над точкой севера? Чему равна полуденная и полуночная высота Солнца на той же широте в дни равноденствий и зимнего солнцестояния?
Данные: день летнего солнцестояния; hв = = +72°50′ N; δ = +23°27′
Решение. В день летнего солнцестояния полуденное зенитное расстояние Солнца
zв = 90°—hв = 90°—72°50′ N = 17°10′ N,
и так как кульминация происходит к северу от зенита, то δ>φ, и, согласно формуле (6),
φ = δ—zв = +23°27’— 17°10′ = +6°17′.
В дни равноденствий δ = 0°, и, по формулам (5) и (8),
hв = 90°—φ = 90°—6° 17′ = + 83°43′ S и hн= — (90°—φ) = — (90°—6°17′) =- 83°43′ N.
В день зимнего солнцестояния δ=-23°27′, т. е. δ
Задача 28.Определить отношение количества тепла, получаемого от Солнца в полдень дней равноденствий и солнцестояний городами, указанными в задаче 26. Сравнение провести для каждого города в отдельности (по датам) и по городам в каждую дату.
Задача 29.Найти полуденную и полуночную высоту Солнца в дни равноденствий и солнцестояний на земном экваторе, на тропиках, на полярных кругах и географических полюсах.
Задача 30.Определить отношение количества тепла, получаемого в полдень дней равноденствий и солнцестояний местами земной поверхности, указанными в предыдущей задаче. Сравнение провести для каждого места (в различные даты) и по местностям (в каждую дату).
Задача 31.На каких географических параллелях Солнце не восходит, проходит в зените и не заходит в дни, когда его склонение равно +21°19′ и —16°43′?
Задача 32.В какие дни года Солнце проходит в зените и надире экватора, тропиков и земных параллелей с географической широтой +7°48′ и —18°35′? (Некоторые даты следует установить по астрономическому календарю-ежегоднику.)
Задача 33.На какой географической широте Солнце кульминирует в день летнего солнцестояния на зенитном расстоянии в 10°41′ к северу от зенита? Чему равна полуденная и полуночная высота Солнца на той же широте в дни равноденствий и солнцестояний?
Задача 34.Решить предыдущую задачу при том же полуденном зенитном расстоянии Солнца, но к югу от зенита.
Задача 35.Найти планетографическую широту* тропиков и полярных кругов на планетах Марсе, Юпитере и Уране, если наклон оси Марса равен 24°48′, оси Юпитера 3°07′, а оси Урана 98° (наклон больший 90° означает обратное вращение планеты).
* Угловое расстояние от экватора планеты, аналогичное географической широте на Земле.
Задача 36.По результатам предыдущей задачи отметить особенности расположения тропиков и полярных кругов в сравнении с земными и определить пределы изменения склонения Солнца в небе этих планет.
Задача 37.Вычислить отношение количества тепла, получаемого от Солнца в полдень дней равноденствий и летнего солнцестояния экватором, северным тропиком и северным полярным кругом Урана и выяснить условия освещения различных зон этой планеты на протяжении периода ее обращения вокруг Солнца, близкого к 84 годам. Наклон оси планеты равен 98°.
Задача 38.При каком склонении Солнца наступают белые ночи в Ленинграде (ср = +59°57′) и Архангельске (φ= +64°34′)? Возможны ли в этих городах полярные дни и полярные ночи?
Задача 39.По результатам предыдущей задачи и астрономическому календарю-ежегоднику определить длительность периода белых ночей в тех же городах.
Задача 40.Воспользовавшись астрономическим календарем-ежегодником, найти длительность периода белых ночей и продолжительность полярного дня и полярной ночи в Мурманске (φ = +68°59′) и Хатанге (φ = +71°58′) и определить наибольшую полуденную и полуночную высоту Солнца в этих городах.
Задача 41.До каких географических параллелей распространяются границы полярного дня, полярной ночи, белых и темных ночей в дни равноденствий и солнцестояний?
Задача 42.На каких географических параллелях начинаются и оканчиваются периоды белых ночей, полярный день и полярная ночь при склонениях Солнца δ = +10° и δ = = +21°? Примерно в какие дни года это происходит?
Ответы — Видимое годовое движение Солнца
Системы счета времени
Звездное время S измеряется часовым углом tγ точки весеннего равноденствия и поэтому всегда S = tγ У небесного светила с прямым восхождением α часовой угол
Звездное время S в пункте с географической долготой λ связано со звездным гринвичским временем S0 равенством
причем λ отсчитывается к востоку от Гринвича и выражается в часах, минутах и секундах времени. Для перевода градусных единиц в единицы времени существуют таблицы.
В один и тот же физический момент звездное время S1 и S2 в двух пунктах различается на разность географической долготы λ1 и λ2 этих пунктов, т. е.
Используемые в практической жизни средние солнечные сутки продолжительнее звездных суток на 3м56с,6
Местное среднее время
Tλ =T 
+η, (16)
где η — уравнение времени, a T —истинное солнечное время, измеряемое часовым углом Солнца, увеличенным на 12ч, т. е.
Τ =t +12ч. (17)
Местное среднее время Tλ1 и Tλ2 двух пунктов связано между собой равенством:
Tλ1 — Tλ2 = λ2—λ1, (18)
а со средним гринвичским временем T0 (называемым всемирным временем)—равенством
В практической жизни используется либо поясное время
либо декретное время
Tд = Tn + 1ч=T0+n+1ч, (21)
где n — номер часового пояса, равный целому числу часов.
Для двух пунктов, расположенных в разных часовых поясах n1 и n2,
Tд2 —Tд1 = Τn2 -Тn1 =n2-n1 (22)
Если система счета времени не указана, то всегда подразумевается время, действующее на данной территории.
Показание часов Тч (или Sч) не всегда соответствует моменту точного времени Τ или S. Разность
u = Т—Тч или us=S — Sч (23)
называется поправкой часов, зная которую можно определять точное время по неверно идущим часам.
Пример 1.Определить звездное время в пунктах с географической долготой 2ч23м37с и 7ч46м20с в момент, когда в пункте с географической долготой 80°05′,5 у звезды Веги (α Лиры) часовой угол равен 4ч29м48с. Прямое восхождение Веги α=18ч35м15с.
Данные: λ1 = 2ч23м37c; λ2=7ч46м20с; λ3 = 80°05′,5;
Вега, α=18ч35м15с, t = 4ч29м48c.
Решение. Пользуясь таблицей 2, выражаем географическую долготу третьего пункта в единицах времени: λ3=80°05′,5 = 5ч20м22с.
Согласно формуле (13), звездное время в третьем пункте (с λ3)
Из формулы (15) следует, что в первом пункте (с λ1) звездное время
S1=S3+(λ1-λ3) — 23ч05м03с + (2ч23м37с—5ч20м22с) = 20ч08м18с;
во втором пункте (с λ2) звездное время
S2 = S3+ (λ2—λ3) =23ч05м03с+ (7ч46м20с—5ч20м22с) = 25ч31м01с,
т. е. в этом пункте начались уже новые звездные сутки (но не календарные сутки), и там S2=1ч31м01c.
При другом ходе решения используется формула (14).
Пример 2.Некоторый пункт с географической долготой 5ч34м находится в пятом часовом поясе. Найти местное среднее, поясное и декретное время этого пункта в истинный полдень 27 октября, если в этот день уравнение времени равно —16м.
Данные: λ=5ч34м, n=5; 27 октября η = —16м.
Решение. В истинный полдень истинное солнечное время T =12ч00м. Согласно формулам (16), (19), (20) и (21), 27 октября местное среднее время
Τλ =T +η=12ч00м—16м=11ч44м, поясное время
Tn = Tλ + (n—λ) = 11ч44м—34м=11ч10м и декретное время
Задача 43.Определить звездное время в моменты верхней и нижней кульминации звезды Фомальгаута (α Южной Рыбы), прямое восхождение которой 22ч54м53с.
Задача 44.Найти звездное время в моменты, в которые часовой угол звезды Ригеля (β Ориона) соответственно равен —3ч17м43с и 1ч42м29с. Прямое восхождение этой звезды 5ч12м08с
Задача 45.Определить звездное время в пунктах с географической долготой 2ч13м23с и 84°58′ в момент, когда в пункте с долготой 4ч37м11с звезда Кастор (α Близнецов) находится в верхней кульминации. Прямое восхождение Кастора 7ч31м25с.
Задача 46.Решить предыдущую задачу для тех же пунктов, но для момента времени, в который звезда Капелла (а Возничего) находится в нижней кульминации в Иркутске (λ=6ч57м05с). Прямое восхождение Капеллы 5ч13м00с.
Задача 47.Вычислить часовые углы звезд Алголя (β Персея) и Альтаира (а Орла) в 8ч20м30с по звездному времени. Прямое восхождение этих звезд соответственно равно 3ч04м54с и 19ч48м21с. Часовые углы выразить в градусных единицах.
Задача 48.Прямое восхождение звезды Миры (о Кита) 2ч16м49с, Сириуса (а Большого Пса) 6ч42м57с и Проциона (а Малого Пса) 7ч36м41с. Чему равны часовые углы этих звезд в моменты верхней и нижней кульминации Сириуса?
Задача 49.Найти часовые углы звезд Кастора (а Близнецов) и Шеата (β Пегаса) в момент, когда часовой угол звезды Беги (а Лиры) равен 4ч15м10с. Прямое восхождение Кастора 7ч31м25с, Беги 18ч35м15с и Шеата 23ч01м21с.
Задача 50.Часовой угол звезды Миры (о Кита) в Гринвиче равен 2ч16м47с. Определить в этот момент звездное время в пунктах с географической долготой 2ч03м02с и 54°44′,5. Прямое восхождение Миры 2ч16м49с.
Задача 51.Найти звездное время и часовой угол звезды Мицара (ζ Большой Медведицы) в Гринвиче и в пункте с географической долготой 6ч34м09с в тот момент, когда в Якутске (λ=8ч38м58с) часовой угол звезды Альдебарана (а Тельца) 329°44′. Прямое восхождение Мицара 13ч21м55с, а Альдебарана 4ч33м03с.
Задача 52.Какое прямое восхождение у звезд, находящихся в верхней и нижней кульминации в двух различных пунктах наблюдения, если в одном из них, расположенном восточнее другого на 36°42′, часовой угол звезды Проциона (а Малого Пса) равен —2ч16м41с? Прямое восхождение Проциона 7ч36м41с.
Задача 53.На каких географических меридианах звездное время соответственно равно 22ч48м30с и 7ч36м34с, если в местности с географической долготой 5ч31м40с звезда
Капелла (α Возничего) имеет часовой угол — 2ч39м08с? Прямое восхождение Капеллы 5ч13м0с.
Задача 54.Через какие интервалы звездного времени после верхней кульминации звезды β Льва с прямым восхождением 11ч46м31с звезда α Гидры будет находиться в верхней кульминации, в нижней кульминации и занимать положение при часовом угле 4ч25м16с? Прямое восхождение α Гидры 9ч25м08с.
Задача 55.В момент верхней кульминации звезды Геммы (а Северной Короны), прямое восхождение которой 15ч32м34с, часы, идущие по звездному времени (звездные часы), показывали 15ч29м42с. Найти поправку часов и их показание при часовом угле той же звезды, равном 1ч20м50с.
Задача 56.В момент верхней кульминации звезды Альдебарана (а Тельца) с прямым восхождением 4ч33м03с звездные часы показывали 4ч52м16с, а в такой же момент следующей ночи их показание было 4ч51м04с. Вычислить поправки звездных часов в моменты наблюдений, а также их суточный и часовой ход (т. е. изменение поправки за сутки и за один час).
Задача 57.В момент верхней кульминации звезды ε Большой Медведицы с прямым восхождением 12ч51м50с звездные часы показывай 12ч41м28с, а в момент последующей нижней кульминации той же звезды их показание было 0ч41м04с. При каких показаниях тех же часов звезда β Малой Медведицы проходила обе кульминации, если, ее прямое восхождение равно 14ч50м50с?
Задача 58.Найти среднее, поясное и декретное время в пунктах с географической долготой 4ч43м28с и 9ч18м37с в момент 6ч52м06с по среднему гринвичскому времени. Первый пункт находится в пятом, а второй — в десятом часовом поясе.
Задача 59.Определить среднее, поясное и декретное время в пунктах с географической долготой 5ч12м56с и 7ч51м22c если в этот момент в третьем пункте часы показывали 17ч31м44с по среднему времени, а географическая долгота третьего пункта равна 6ч27м36с. Первый пункт находится в пятом, а второй — в восьмом часовом поясе.
Задача 60.Найти разность между поясным и средним, а также между декретным и средним временем в пункте с географической долготой 7ч18м58с, расположенном в седьмом часовом поясе.
Задача 61.Определить последовательность наступления одноименных моментов по среднему, поясному и декретному времени в Баку (λ=3ч19м, n=3) и Новосибирске (λ=5ч32м, n=6).
Задача 62.В какие моменты времени по различным системам счета наступают истинный полдень и истинная полночь в Ростове-на-Дону (λ=2ч39м, n=3) и Оренбурге (λ=3ч41м, n=4) в дни, когда уравнение времени соответственно равно +12м и —15м?
Задача 63.Точные городские часы Красноярска (n = 6) показывают 7ч32м вечера. Какое в этот момент среднее, поясное и декретное время в Киеве (λ=2ч02м, n=2) и Хабаровске (λ=9ч00м, n=9)?
Задача 64.После месячного полета на научной космической станции «Салют-4» космонавты А. А. Губарев и Г. М. Гречко 9 февраля 1975 г. в 14ч03м по московскому времени приземлились северо-восточнее Целинограда. Сколько времени было в этот момент в Целинограде (n = 5) и Казани (n=3)? Москва находится во втором часовом поясе.
Задача 65.Лунное затмение 18 ноября 1975 г. началось в 20ч38м,5 и окончилось 19 ноября 1975 г, в 0ч08м,2 по всемирному времени. В какие даты и моменты времени оно началось и окончилось в Краснодаре (n=3), Ташкенте (n = 5) и Иркутске (n = 7)?
Задача 66.В 1974 г. летнее солнцестояние наступило 21 июня в 18ч38м по всемирному времени. Когда оно наступило по времени городов, указанных в предыдущей задаче?
Задача 67.В момент передачи из Москвы (n = 2) 12-часового радиосигнала точного времени часы в одном из учреждений Томска (λ=5ч40м, n = 6) показывали 16ч12м. Вычислить поправку этих часов к местному среднему и принятому времени Томска и Красноводска (λ=3ч32м, n=4) и найти показания тех же часов в 19ч0м по времени каждого города.
Задача 68.Самолет вылетел из Свердловска (n = 4) в 11ч20м и прибыл без опоздания в Иркутск (n = 7) в 17ч45м. Сколько времени летел самолет и какие моменты вылета и прибытия указаны в расписании Аэрофлота?
Задача 69.Телеграмма отправлена из Нерчинска (n = 8) в 7ч40м вечера по городским часам и доставлена адресату в Смоленске (n=2) в тот же день в 16ч20м по времени этого города. Сколько времени шла телеграмма и какие моменты времени отправки и доставки отмечены на ней?
Ответы — Системы счета времени
Источник