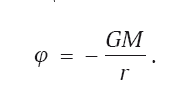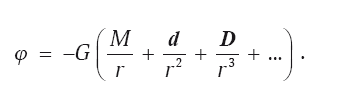Генерация гравитационного излучения
Генерация гравитационного излучения
Гравитационное излучение чрезвычайно слабое. Это связано со слабостью гравитационного взаимодействия в природе. Например, электромагнитная константа связи (ее называют постоянной тонкой структуры) ?=e 2 /hc ? 1/137, где используются заряд электрона, постоянная Планка и скорость света. В то же время аналогичная безразмерная константа связи гравитационного взаимодействия имеет порядок ? G = Gm p 2 /hc = (m p/m Pl) 2 ? 10 –38 , где используются масса протона и планковская масса. В отличие от электромагнитного излучения, когда каждый атом может излучить фотон, и его можно зарегистрировать, гравитационное излучение формируется большим количеством атомов, электронов и т. д. и становится существенным при несимметричном движении больших масс вещества (отдельных объектов) в целом.
Продолжая сравнение с электродинамикой, вспомним, что электромагнитное излучение генерируется переменным дипольным моментом. А при каких условиях возникает гравитационное излучение? Чтобы ответить на этот вопрос, объясним, что такое дипольный момент и моменты других порядков массивного тела.
Вспомним, что потенциал точечной массы в теории Ньютона
Если вместо точки взять сферическое тело (однородный шар) той же массы M с центром, где раньше была точка, то значение потенциала вне тела не изменится.
При несферичности рассматриваемого тела выражение для потенциала изменится, и изменения будут связаны непосредственно с отклонениями от сферичности. Величину отклонения можно представить так. Если сферическую составляющую принять за исходную симметрию, то первая степень отклонения (грубая) – дипольная, следующая (более «тонкая») – квадрупольная, и т. д. Тогда значение потенциала в выбранной точке можно представить в виде:
Здесь d – дипольный момент, а D – квадрупольный. Формула является символической: в ней не учтены коэффициенты, а также векторный и тензорный характер некоторых величин. Но она показывает, что при удалении от источника каждый из последующих членов ряда дает все меньший вклад в формирование потенциала.
В электродинамике излучение определяется изменением дипольнного момента (рис. 10.1) В гравитации дипольный момент, который является вектором, определяется следующим образом: из начала координат к каждому элементу массы ?M проводится радиус-вектор R, после чего величины ?M·R векторно суммируются по всем элементам массы. Ясно, что выбрав начало координат в центре масс, мы получим дипольный момент тождественно равный нулю. Это можно сделать всегда, поскольку в гравитации, в отличие от электромагнетизма, нет противоположных зарядов (нет отрицательных масс). Следовательно, не может быть и гравитационного излучения, связанного с дипольным моментом.
Гравитационное излучение возникает при изменении квадрупольного момента – D. Вспомним о моменте инерции, который является мерой инертности тела во вращательном движении, точно так же, как инертная масса – мерой инерции в поступательном движении. Квадрупольный момент – это момент инерции из которого исключена шаровая составляющая, определяющая основной (симметричный) вклад в потенциал.
Если в электродинамике мощность электромагнитного излучения пропорциональна квадрату второй производной по времени от дипольного момента, то в ОТО гравитационное излучение возникает из-за переменной асимметрии, определяемой квадрупольным моментом D, и мощность излучения пропорциональна квадрату третьей производной по времени от D. Значит, как бы тело не было деформировано, оно не излучает, если покоится.
Проиллюстрируем на простых примерах, какие системы излучают гравитационные волны, а какие – нет.
Рассмотрим сначала однородный шар, который пульсирует без изменения сферичности. Излучает ли гравитационные волны такой объект? Ответ – нет. Действительно, если сферичность не нарушена, то из наших рассуждений о потенциале следует, что на любой стадии пульсации квадрупольный момент просто не возникает. Приведем другой пример. Пусть любое аксиально симметричное однородное тело типа дыни вращается, а ось вращения совпадает с осью симметрии. Хотя «дыня» и имеет квадрупольный момент, но при таком вращении он не будет меняться. Значит, снова не будет излучения.
Теперь приведем простые примеры излучающих систем. Рассмотрим два тела одинаковой массы m и незначительных габаритов, соединенные пружинкой длины l. Выберем направление одной из осей координат, скажем 0х, вдоль пружины, а середину пружины – за начало координат. У такой системы будет единственная независимая ненулевая компонента D. В состоянии покоя это D xx = ml 2 . Через нее определяются D yy = D zz = —D xx/2. Теперь заставим грузы колебаться относительно своих положений равновесия с амплитудой L и частотой. Тогда компоненты квадрупольного момента станут переменными:
Соотношение D yy = D zz = —D xx/2 сохранится. Производная по времени третьего порядка этих величин ненулевая, значит, система излучает гравитационные волны.
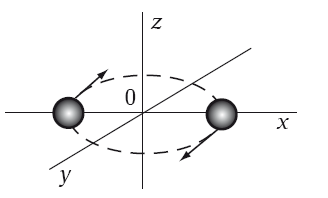
Другой пример ближе к жизни, и мы рассмотрим его подробнее. Пусть две звезды одинаковой массы m, вращаются по одной и той же окружности вокруг общего центра масс. Они все время находятся друг против друга на расстоянии 2R (рис. 10.3). Пусть плоскость орбиты совпадает с плоскостью x0y, а угловая частота вращений равна ?, она связана с орбитальным периодом как T = 2?/?. Тогда ненулевыми компонентами квадрупольного момента являются:
Рис. 10.3. Модель двух звезд
Начальное состояние соответствует t = 0, массы расположены на оси 0x. В данный момент компоненты квадруполя будут такими же, как в модели с пружинкой, т. е. независимой является только одна компонента.
Конечно, и такая система должна излучать. Поскольку движение обусловлено гравитационным взаимодействием, то и R связаны уравнением m 2 R = Gm 2 /4R 2 . Тогда, после усредненияя по периоду и представления через R, мощность гравитационного излучения выражается формулой:
Система излучает тем интенсивнее, чем меньше R (или чем больше частота вращения, как следует из их уравнения связи).
Чтобы проиллюстрировать насколько мало гравитационное излучение, приведем следующий пример. В Солнечной системе, наибольшая мощность гравитационного излучения возникает в паре Солнце + Юпитер. Это излучение можно рассчитать по аналогичной формуле. В результате получим примерно 5 кВт (это всего лишь мощность пяти больших бытовых кипятильников советских времен). Энергия, теряемая Солнечной системой на гравитационное излучение за год, совершенно ничтожна по сравнению с кинетической энергией этих тел.
Необходимо сказать несколько слов о направленности гравитационного излучения. В случае с грузами на пружинке по ее оси вообще нет излучения, а максимум – в направлении перпендикулярном пружинке. В случае кругового движения интенсивность излучения в направлении перпендикулярном плоскости орбиты в несколько раз больше, чем в направлениях, лежащих в плоскости. Связаны эти особенности с тем, что излучаемая гравитационная волна является поперечной.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
2. Теория излучения черного тела. Квант действия Планка
2. Теория излучения черного тела. Квант действия Планка Начало развитию квантовой теории положили относящиеся к 1900 г. работы Макса Планка по теории излучения черного тела. Попытка построить теорию излучения черного тела на основе законов классической физики привела к
1. Трудность согласования квантовой теории и теории излучения
1. Трудность согласования квантовой теории и теории излучения Электромагнитная теория, дополненная теорией электронов Лоренца, дает совершенно ясную и точную картину излучения, испускаемого системой движущихся зарядов. Если заданы структура и закон движения системы
Теория гравитационного поля
Теория гравитационного поля Эйнштейну, который сформулировал свой физический принцип, не зная о трудах Римана, недоставало математического языка и способностей, необходимых для выражения этого принципа. Три долгих, обескураживающих года (1912–1915) он провел в
Глава 8 Ядерные источники энергии излучения звезд
Глава 8 Ядерные источники энергии излучения звезд В § 3 мы уже говорили о том, что источниками энергии Солнца и звезд, обеспечивающими их светимость в течение гигантских «космогонических» промежутков времени, исчисляемых для звезд не слишком большой массы миллиардами
Глава 9 Проблемы нейтринного излучения Солнца
Глава 9 Проблемы нейтринного излучения Солнца До сравнительно недавнего времени одна из важнейших проблем астрономии — проблема внутреннего строения и эволюции звезд решалась совместными усилиями астрофизиков-теоретиков и астрономов-наблюдателей. Как уже
56. Тепловые излучения тел
56. Тепловые излучения тел Из всего многообразия электромагнитных излучений, видимых или невидимых человеческим глазом, можно выделить одно, которое присуще всем телам. Это излучение нагретых тел, или тепловое излучение. При тепловом излучении энергия переносится от
Источники гравитационного излучения
Источники гравитационного излучения – Возьмем две звезды, разгоним почти до скорости света и столкнем. Что произойдет? – Нехилый коллайдер получится… Из форума Слабость гравитационного излучения оставляет мало шансов для его регистрации. Где же искать подходящие
Роль вынужденного излучения в теории дисперсии света
Роль вынужденного излучения в теории дисперсии света Используя результаты Эйнштейна, физики-теоретики смогли построить квантовые теории рассеяния света и дисперсии.Как мы уже говорили о преломлении света призмой, лучи света, которые относятся к различному цвету,
Генерация от ускоренных электронов
Генерация от ускоренных электронов В начале 1951 г. физик Ганс Мотц (1909—1987) предложил новый способ получения излучения на миллиметровых и субмиллиметровых длинах волн, который не включал явного упоминания процессов инверсии населенности или вынужденного излучения, даже
Источник
Солнечная энергия. Цифры и факты
Основные характеристики солнечного света
Освещенность (усредненная мощность солнечного излучения, измеренная в верхней атмосфере Земли перпендикулярно солнечным лучам): 1366 Вт на квадратный метр (или 1361, в соответствии с НАСА).
«Стандартное солнце» (пиковая мощность излучения, которая достигает поверхности Земли на уровне моря в районе экватора в безоблачный полдень): 1000 Вт/м 2 , или 1 кВт/м 2 .
Это значение обычно используется в характеристиках фотоэлектрических систем. Здесь и далее все цифры приведены для поверхностей, оптимально расположенных относительно солнца (перпендикулярно лучам) в соответствии с широтой. Для горизонтальных поверхностей вы получите меньше солнечного света: чем дальше от экватора, тем ниже плотность солнечной энергии.
Инсоляция (среднее количество часов «стандартного солнца» на протяжении суток): от 4–5 солнечных часов на северо-востоке США до 5–7 часов на юго-западе. Инсоляция часто указывается в кВт·ч, численно вытекая из значения «стандартного солнца» в 1 кВт.
Общее количество излучаемой энергии солнечного света в день на м 2 на уровне моря: (энергия за день) = 1 кВт·ч × (инсоляция в часах). Учитывая среднюю инсоляцию в США, равную 5 солнечным часам, это значение обычно равно 5 кВт·ч/м 2 .
Солнечная мощность, усредненная за весь день: Wattsaverag = (энергия за день)/24. Для инсоляции в 5 кВт·ч мощность, усредненная за весь день – 5000 Вт/24 = 208 Вт/м 2 . Обратите внимание, что только небольшая часть этой энергии может быть преобразована в электричество из-за не очень высокой эффективности фотоэлектрических систем.
Типовые характеристики фотоэлектрических систем
Средний КПД распространенных коммерческих солнечных панелей: на кристаллическом кремнии (CSI) – 12–17%; тонкопленочных (из аморфного кремния и других материалов) – 8–12%.
Мощность, генерируемая панелью в один квадратный метр: PVwatts = (солнечная мощность) × (средний КПД), где КПД преобразуется в десятичное число.
Пиковая мощность в безоблачный полдень: PVwatts-peak = 1000 Вт × КПД. Как правило, пиковая мощность равна 120170 Вт/м 2 для CSi и 80–120 Вт/м 2 для тонких пленок (TF).
Суммарное усредненное количество энергии, производимой панелью в один м 2 за день: PVday = PVwatts-peak × (Инсоляция в часах). Для инсоляции в 5 часов это значение будет 0.6–0.85 кВт/м 2 для CSi и 0.4–0.6 кВт/м 2 для TF.
Выработанная энергия панели, усредненная за весь день: PVwatts-average = PVday/24. Это примерно 25–35 Вт/м 2 для CSi и 17–25 Вт/м 2 для TF.
Общая энергия, генерируемая фотоэлектрическим модулем на м 2 в год: PVyear = (полная энергия в день) × 365, которая будет равна примерно 219–310 кВт·ч для CSi и 146–219 кВт·ч для TF. Обратите внимание, что инверторы имеют эффективность 95–97%, поэтому фактической электроэнергии будет на 5% меньше.
Ожидаемая стоимость электроэнергии с одного м 2 , сэкономленной за год: Saving = PVyear × 0.95 × (стоимость кВт·ч), где 0.95 – КПД преобразователя и потери в проводах.
В среднем в США стоимость одного кВт·ч электроэнергии равна $0.12, это дает в год $24–35 для CSi и $17–24 для тонких пленок. Таким образом, в лучшем случае, можно будет сэкономить $35 в год на 1 м 2 панели. Эта цифра относится к высокоэффективной системе с номинальной мощностью 170 Вт/м 2 . Учитывая тот факт, что в настоящее время стоимость типичной фотоэлектрической системы составляет $8000 на 1000 Вт, такие установки будут стоить 170/1000 × $8,000 = $1,360 за м 2 . Это означает, что в нашем примере, гипотетический срок окупаемости будет 1360/35 = 39 лет. Никакое оборудование не сможет так долго функционировать. Скидки и кредиты могут сократить это время более чем на половину, однако, все равно, для среднестатистического домашнего хозяйства установка солнечной панели, скорее всего, не окупится. Конечно, это всего лишь пример. В районах с другой инсоляцией и другими затратами на установку срок окупаемости может быть выше или ниже.
Краткая информация о Солнце
- Диаметр: 1,392,000 км;
- Масса: 1,989,100 × 10 24 кг;
- Температура на поверхности:
5,700 °С;
385 млрд. МВт);
Перевод: Андрей Гаврилюк по заказу РадиоЛоцман
Источник