Момент импульса земля луна
Приливная эволюция системы Земля-Луна, происходит по причине передачи момента импульса быстро вращающейся Земли орбитальному движению Луны посредством гравитационно-приливного взаимодействия. Приливный горб, деформирующий поверхность Земли оседает не сразу, выходя из подлунной точки, а некоторое время тянет Луну за собой, разгоняя ее на орбите и притормаживая вращение Земли.
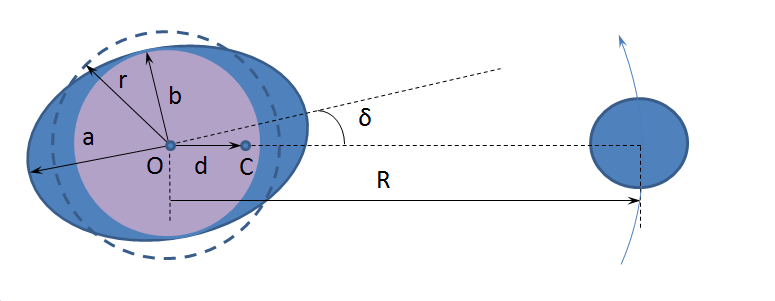
Рассчитаем момент импульса системы Земля-Луна (СЗЛ), полагая, что оба тела движутся по круговым орбитам, ось вращения Земли перпендикулярна плоскости ее орбиты. Луне принадлежит часть момента импульса:
$L_m=M_m (R-d)^2 \Omega$, (1)
где $M_m$ — масса Луны, $R$- расстояние между центрами Земли и Луны, $d$ — расстояние от центра Земли до барицентра СЗЛ, равное
$\Omega$ — угловая скорость вращения СЗЛ вокруг ее барицентра, которая равна
где $M_e$ — масса Земли, $G$ — гравитационная постоянная.
В итоге, момент импульса Луны в ее движении по орбите равен:
Поскольку суммарный момент импульса СЗЛ сохраняется, изменение момента импульса Луны зависит от приливного момента, действующего на Землю, взятого с обратным знаком:
В работе [1] было показано, что приливный момент, тормозит вращение Земли:
где $m$ — точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, $r$ — радиус Земли, $ \delta $ — смещение приливного горба относительно подлунной точки.
В результате приливного взаимодействия уровенная поверхность Земли принимает форму эллипсоида вращения[2], полуоси которого равны:
Результирующий приливный момент определяется массой, находящейся за пределами сферы радиуса $b$. Масса приливного горба, таким образом, равна
где $\rho$ — плотность вещества приливного горба, $\Delta V$ — разность объемов приливного эллипсоида и сферы радиуса $b$.
Точечная масса, сосредоточенная в вершине приливного горба, создающая момент, равный реально действующему, очевидно меньше массы всего приливного горба и равна:
где $k_m Войдите на сайт для отправки комментариев
Источник
Момент импульса земля луна
Как известно, Луна удаляется от Земли. Когда это началось, и как долго это будет происходить? И что будет потом? На эти вопросы нет однозначного ответа. Вращательная энергия Земли посредством приливного взаимодействия передается Луне, и та удаляется. Приливное трение «съедает» огромное количество механической энергии, поэтому полная механическая энергия системы Земля-Луна не сохраняется. Однако, выполняется закон сохранения момента импульса. Он не чувствителен к диссипативным процессам!
Представим себе два одинаковых диска, один из которых раскрутили, а потом прижали ко второму. Первый диск будет скользить по второму, постепенно приводя его в движение, но теряя при этом в скорости вращения. В какой-то момент угловые скорости обоих дисков станут равными, и диски будут вращаться как одно целое (Рис. 1).
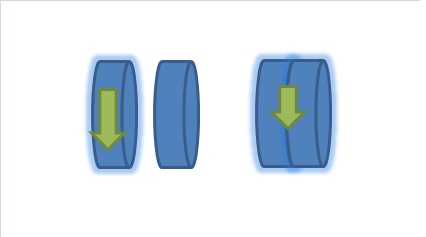
Закон сохранения механической энергии в данном случае не выполняется, поскольку трение рассеивает часть механической энергии в тепло. Зато выполняется закон сохранения момента импульса, который и позволит нам рассчитать потери энергии и конечную скорость вращения дисков.
В начале, первый диск обладает моментом импульса
и кинетической энергией
В конце суммарный момент импульса дисков равен
а их энергия равна
Запишем закон сохранения момента импульса:
На трении будет потеряна
$\Delta T=T_1-T_2=\frac<1><2>I\omega_1^2-\frac<1><4>I\omega_1^2=\frac<1><2>T_1$ (7)
ровно половина кинетической энергии первого диска.
Обратимся теперь к системе Земля-Луна. Допустим, что Луна движется по круговой (точнее очень близкой к круговой в любой момент времени) орбите вокруг Земли, и не испытывает никаких гравитационных воздействий, кроме приливного взаимодействия с Землей. Ось вращения Земли о ось орбитального движения Луны совпадают.
В такой модели Луна удаляется от Земли, угловая скорость ее орбитального движения и угловая скорость вращения Земли уменьшаются, пока не станут равными в резонансе 1:1.
Запишем закон сохранения момента импульса для системы Земля-Луна:
$C\omega_0+M r_0^2\omega_1=C\omega+M r^2\omega$, (8)
где $C=8.039\cdot10^ <37>$ кг м 2 — момент инерции Земли, $\omega_0=7.292\cdot10^<-5>$ — угловая скорость вращения Земли в настоящее время, $M= 7.3477\cdot10^<22>$ кг — масса Луны, $r_0 = 3.844\cdot10^8$ м — среднее расстояние от Земли до Луны в настоящее время, $\omega_1= 2.649\cdot10^<-6>$ рад/с — угловая скорость орбитального движения Луны в настоящее время, $\omega$ — резонансная угловая скорость вращения Земли (и обращения Луны по орбите), $r$ — расстояние Земля-Луна в момент достижения резонанса 1:1.
Разделим левую и правую часть (8) на $ r_0^2 \omega_1 $ и вводя обозначение
Введем новые обозначения
Согласно третьему закону Кеплера
или, в наших новых обозначениях
Подставляя $x$ и $y$ в (10), получим:
Это выражение эквивалентно уравнению четвертой степени относительно $x$.
можно видеть на Рис. 2.
.jpg)
Найдем корни уравнения $f(x)=0$ численно:
Таким образом, Луна сможет удалиться не более чем на $ 5.532\cdot10^8$ м, что намного меньше сферы действия Земли относительно Солнца ($9.25\cdot10^8$ м).
Сутки при этом станут в 47 раз длиннее, чем сейчас и будут равны лунному месяцу.
Интересно, что резонанс 1:1 возможен с точки зрения математики и на расстоянии в 2.3 земных радиуса, при угловой скорости Земли в 5 раз большей, чем сейчас (т.е. сутки менее 5 часов).
Такая ситуация сомнительна или даже невозможна с точки зрения физики, поскольку Луна была бы разорвана приливными силами, а Земля силами инерции. Другое дело, если Земля и Луна представляли собой тогда аморфные тела – два сгустка материи, вращающиеся как одно целое.
Тот же закон сохранения момента импульса (10) поможет нам заглянуть в прошлое.
Обозначим $\omega_m$ — угловую скорость орбитального движения Луны, а $\omega_e$ — угловую скорость вращения Земли.
По закону сохранения момента импульса:
$\omega_e=\omega_1 r_0^2\left ( \frac
По третьему закону Кеплера:
$\omega_m=\omega_1 x^<-3/2>$ (18)
Зависимость этих угловых скоростей показана на Рис. 3.
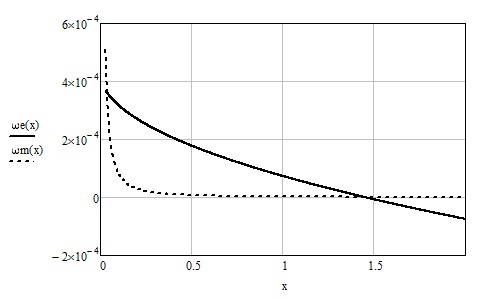
Глядя, на эти графики, можно подумать, что чудовищные приливные силы довольно быстро отдалили Луну от Земли и сейчас мы наблюдаем угасание процесса ее ухода. Повторюсь, что данная ситуация маловероятна.
Также можно видеть, что после прохождения точки резонанса 1:1 Земля начнет вращаться в обратную сторону. Это тоже маловероятно, поскольку в точке резонанса перестанет действовать механизм передачи момента импульса от Земли к Луне, исчеснет трансверсальная сила от приливных горбов, разгоняющая Луну.
- Ingus’s блог
- Войдите на сайт для отправки комментариев
- 4015 просмотров
Уважаемый Ingus! Модель интересная. Но почему не учитывается момент импульса и энергия вращения самой Луны? Тем более, что именно это вращение порождает диссипацию внутри Луны. По этой причине, как считается, Луна повернута к нам одной и той же стороной, что минимизирует приливную диссипацию. По моему, модель надо подправить. А так интересно.
Момент импульса Луны относительно ее оси вращения составляет $1.9\cdot10^<-6>$ суммарного момента импульса системы Земля-Луна. Стоит ли о нем говорить?
Такое значение момента импульса у Луны сейчас. А раньше, когда Луна была ближе? Считается, что Луна раньше находилась гораздо ближе к Земле. Модель твоя должна была бы объяснить удаление Луны с более близкой позиции к современной. Я об этом говорю.
Виктор Михайлович! Спасибо, что обратили внимание. Я как раз над этим думаю. Когда-то Луна вращалась вокруг своей оси ( в какую сторону кстати?). Нужно ввести ее момент в модель, чтобы посмотреть значимость. Сделаю.
Иван! Луна и сейчас вращается, но в резонансе с орбитальным периодом 1:1. Вполне возможно, что система в конце концов должна придти в состояние с резонансом 1:1 и к вращению Земли и Луны одновременно. Луна в этом смысле уникальный случай. Слишком большая масса для спутника. В системах больших планет там резонанс 1:1 встречается не так часто. Примером может служить Ганимед, но это случай как раз обратный твоему. Его влияние на вращение Юпитера незначительно. А вот обратный эффект существенный. С Луной, похоже, что-то подобное. Видимо это надо учитывать Твоя модель нравится своей простотой и наглядностью.
Да. Согласен. Не вышел я еще на нужный уровень( Конечно, следовало бы сказать «Раньше Луна вращалась с большей угловой скоростью»
Источник
Формула света
Новая картина Мироздания
Приливные силы
Картинка к этой статье взята из интернета. Там много таких картинок, и во всех содержится одна и та же принципиальная ошибка. Какая? Надеюсь, вы сможете ответить на этот вопрос, прочитав статью.
Уравнения гравитации обратимы во времени. Это означает, что если возможно какое-то движение по орбите, то, возможно и обратное движение по той же самой орбите. То есть, процессы, происходящие под действием гравитации обратимы во времени. И всё-таки, это не совсем так. Когда планеты и спутники находятся близко друг к другу, они ДЕФОРМИРУЮТ друг друга своими гравитационными полями. При такой деформации часть энергии переходит в тепло. А это уже НЕОБРАТИМЫЙ процесс. Поэтому любая гравитационно связанная система постепенно эволюционирует в сторону уменьшения свободной энергии. В дальнейшем, используя простые рассуждения и уравнения, мы сможем понять, в КАКОМ направлении должна эволюционировать любая планетная система. В результате мы сможем ответить на вопрос: КАК образуется планетная система? В результате распада или сжатия вещества?
Самый известный тип необратимого гравитационного взаимодействия – это приливные силы. Познакомимся с ними.
Пусть вокруг планеты по круговой орбите вращается спутник, который повёрнут к ней всегда одной и той же стороной. Поэтому приливные силы, действующие со стороны планеты на спутник, сводятся только к тому, что он немного «вытягивается» в сторону планеты. Например, Луна повёрнута к Земле всегда одной и той же стороной, а её диаметр в направлении Земли немного больше, чем в каком-либо другом направлении. То же самое относится и к спутникам других планет.
Физический смысл этого явления достаточно прост. В центре спутника центробежная сила, вызванная его движением по орбите, в точности уравновешена силой притяжения со стороны планеты. В половине спутника, ближней к планете, центробежная сила меньше силы притяжения, а в дальней половине – наоборот, больше. Эта разность сил и вытягивает спутник:

Соответственно, спутник также «вытягивает» планету вдоль линии, соединяющей планету и спутник, образуя два приливных «горба» на противоположных сторонах планеты.
Если вращение планеты и спутника не синхронно, то возникает так называемое приливное трение, которое либо тормозит, либо ускоряет вращение планеты.
В качестве примера рассмотрим систему Земля-Луна. Луна своим гравитационным полем вытягивает на Земле два приливных горба: на подлунной и противоположной сторонах. Из-за того что Земля вращается вокруг своей оси быстрее, чем Луна по своей орбите, этот горб смещается относительно линии Земля-Луна:
Здесь схематично изображено, как вытянуты Земля и Луна (вид с Северного полюса). На самом деле, они вытянуты намного слабее. Я специально «вытянул» их сильно, чтобы было хорошо видно. Лунные горбы ориентированы строго вдоль линии Земля-Луна. А земные – нет. Потому что Земля вращается вокруг своей оси значительно быстрее, чем Луна движется по орбите. Из-за этого вытянутость (приливные горбы) Земли повернута на некоторый угол (на изображении этот угол также преувеличен). Поэтому Луна вытягивает два новых горба на земной поверхности вдоль линии Земля-Луна. Эти новые горбы снова смещаются из-за вращения Земли и процесс повторяется.
В результате возникают два эффекта.
Из-за постоянного возникновения приливного горба на подлунной и противоположной сторонах Земли создаётся эффект бегущей приливной волны. Она движется против вращения Земли и, соответственно, замедляет её. При этом выделяется энергия в виде тепла. Из-за инерции земной коры приливный горб незначительно сдвинут относительно линии Земля-Луна в направлении вращения Земли. Благодаря этому гравитационные силы, действующие со стороны горба на Луну, ускорят её движение по орбите.
В результате момент импульса Земли уменьшается, а Луны, наоборот, увеличивается. Земля постепенно передаёт энергию своего вращения Луне, которая вследствие этого медленно удаляется от Земли. Стоит отметить, что Земля передаёт Луне только малую часть кинетической энергии, потерянной вследствие действия приливных сил. А бОльшая часть кинетической энергии переходит в тепло, незначительно нагревая Землю.
На это явление можно посмотреть и с другой стороны. Луна вызывает на Земле приливы, энергию которых можно использовать. Ясно, что подобный процесс не может продолжаться вечно. Система Земля-Луна должна терять энергию. Из-за того что приливная волна движется против вращения Земли, она постепенно тормозит Землю, уменьшая её момент импульса. Однако момент импульса замкнутой системы должен оставаться неизменным. Поэтому орбитальный момент импульса Луны увеличивается.
На первый взгляд, это может показаться странным. Действительно, в результате трения, вызванного движением Луны вокруг Земли, Луна не падает на Землю, а, наоборот, удаляется от неё. То есть, её энергия возрастает. Получается, что Луна, совершая работу над Землёй (в том числе, заставляя работать приливные электростанции), увеличивает собственную энергию. Откуда же берётся энергия? Из вращения Земли. Земля постепенно тормозится, и её потерянная кинетическая энергия тратится на приливный нагрев, на работу приливных электростанций и на увеличение гравитационной энергии Луны.
А хватит ли энергии земного вращения на всё это? Да, хватит.
Мы уделяем много времени приливным силам, потому что они очень важны для понимания эволюции Солнечной системы. Образно говоря, это один из немногих ключей, используя которые можно приоткрыть завесу тайны, скрывающую возникновение планет и их спутников.
Итак, вращение Земли замедляется, и её момент импульса уменьшается. Так как общий момент импульса системы Земля-Луна сохраняется (мы не учитываем в данной задаче приливные силы со стороны Солнца), то утраченный Землёй момент импульса в целости сохранности передаётся Луне. Что при этом происходит с полной энергией системы?
Момент импульса пропорционален массе, расстоянию и скорости, а кинетическая энергия – массе и квадрату скорости. Поэтому ясно, что эти величины не смогут сохраняться вместе. Возрастать кинетическая энергия системы не может, поэтому остаётся единственная возможность. Момент импульса всей системы строго сохраняется, а её кинетическая энергия уменьшается. При этом весь недостаток кинетической энергии необратимо переходит в тепло.
Скорость вращения Земли уменьшается, а скорость движения Луны по орбите возрастает. Но так как Луна находится значительно дальше от центра вращения, чем Земля, её скорость возрастает не так сильно, как уменьшается скорость вращения Земли. То есть Земля теряет кинетической энергии значительно больше, чем передаётся Луне по закону сохранения момента импульса. И вся эта разность переходит в тепло. Здесь важно подчеркнуть, что всё это тепло выделяется только внутри и на поверхности Земли. На Луне же никакого нагрева в результате этого процесса не происходит.
Здесь может возникнуть сомнение. Предположим, планета очень массивная, а её спутник – крошечный. В таком случае дополнительная скорость, которую получит спутник в результате действия приливных сил, будет намного больше, чем скорость, потерянная планетой. Так как прибавка скорости пропорциональна переданному моменту и обратно пропорциональна массе спутника. С другой стороны кинетическая энергия пропорциональна квадрату скорости. Не будет ли в этом случае нарушаться закон сохранения энергии? Давайте проделаем расчёты.
Источник