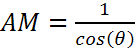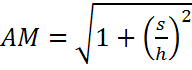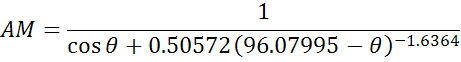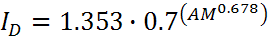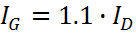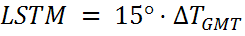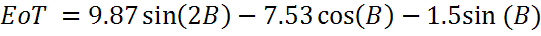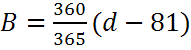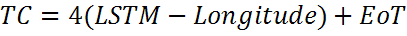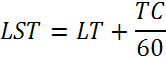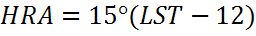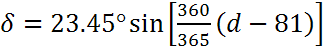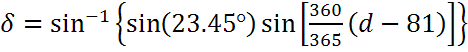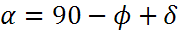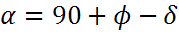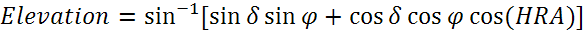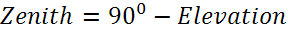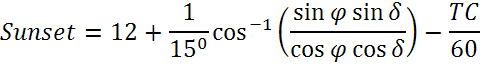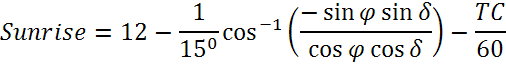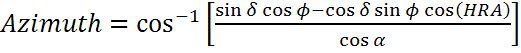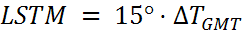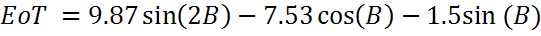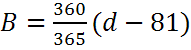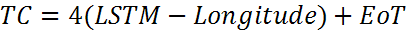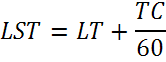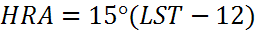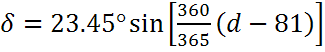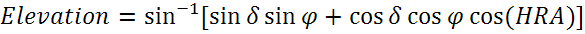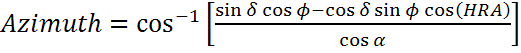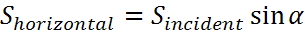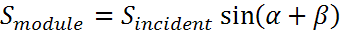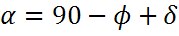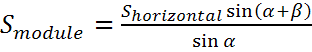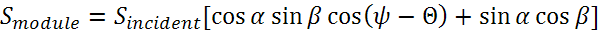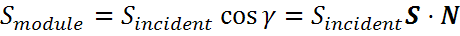Порядок решения некоторых астрономических задач
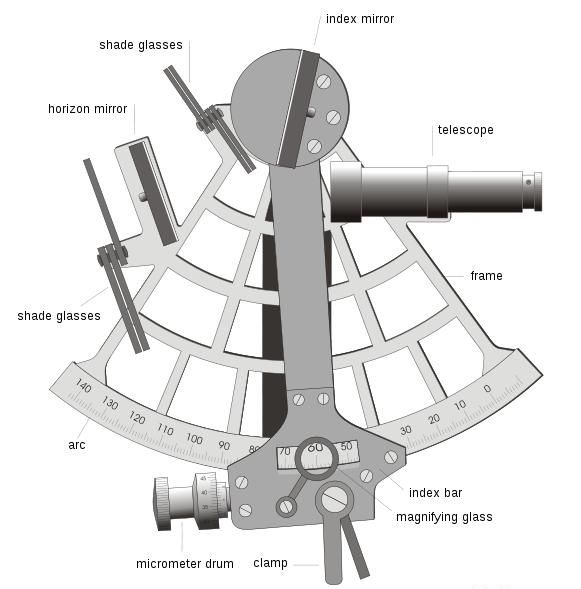
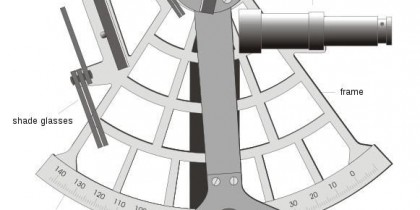
При решении различных задач мореходной астрономии используются следующие основные соотношения и формулы.
Для определения даты на меридиане Гринвича и приближенного всемирного времени Тгр к судовому времени.
Тс прибавляют западный (или отнимают восточный) номер часового пояса: Тгр = Тс + №W, Тгр = Тс — №E.
Для определения всемирного времени Тгр показания хронометра Тхр исправляют его поправкой uхр (и прибавляют 12 ч, если это необходимо): Тгр = Тхр + uхр + (12ч).
При определении местного часового угла tм к гринвичскому часовому углу tгр прибавляют восточную (или отнимают западную) долготу l: tм = tгр+ lW, tм = tгр — lE.
Определяя местный часовой угол звезды tм* , к местному часовому углу точки Овна tмg прибавляют звездное дополнение t*: tм* = tмg+ t*.
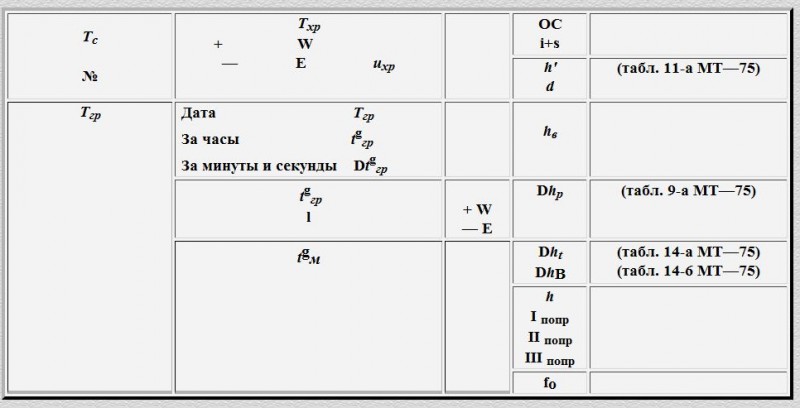
Исправление высот светил:
для получения измеренной высоты светила h’ отсчет навигационного секстана ОС исправляют поправкой индекса i и инструментальной поправкой s:
Для получения видимой высоты светила hв высоту h’ светила исправляют поправкой за наклонение видимого горизонта d:
Чтобы получить истинную высоту светила h, видимую высоту hв исправляют поправками за астрономическую рефракцию Dhr и параллакс Dhp, а для видимых высот до 50° дополнительными поправками за изменение средней астрономической рефракции в зависимости от температуры Dht и давления воздуха DhВ:
h = hв + Dhr + Dhp + Dht + DhВ.
4.2. Определение широты по высоте Полярной звезды
Широту fо рассчитывают по формуле
fо= h + I + II + III,
где h — истинная высота Полярной звезды; I, II, III — поправки, выбираемые из МАЕ.
1. Измеряем секстаном высоту Полярной звезды и одновременно замечаем Tc и отсчет хронометра.
2. Из ежедневных таблиц МАЕ по гринвичской дате и по Тгр выбираем гринвичский часовой угол точки Овна tgгр на табличный момент всемирного времени, ближайший меньший к рассчитанному моменту Тгр.
3. Из основных инерполяционных таблиц (приложение 4 МАЕ), соответствующих минуте всемирного времени Тгр, в графе “Точка Овна” находим полное изменение Dtgгр за минуты и секунды Тгр.
4. Складываем значения величин tgгр и Dtgгр , результат представит значение гринвичского часового угла точки . Овна tgгр для заданного момента Тгр.
5. Полученный гринвичский часовой угол точки Овна tgгр переводим в местный часовой угол tgм по формуле
6. Отсчет секстана ОС исправляем поправками для получения истинной h.
7. Из таблиц МАЕ “Широта по высоте Полярной” выбираем три поправки к высоте Полярной.
Определение широты по меридиональной высоте Солнца
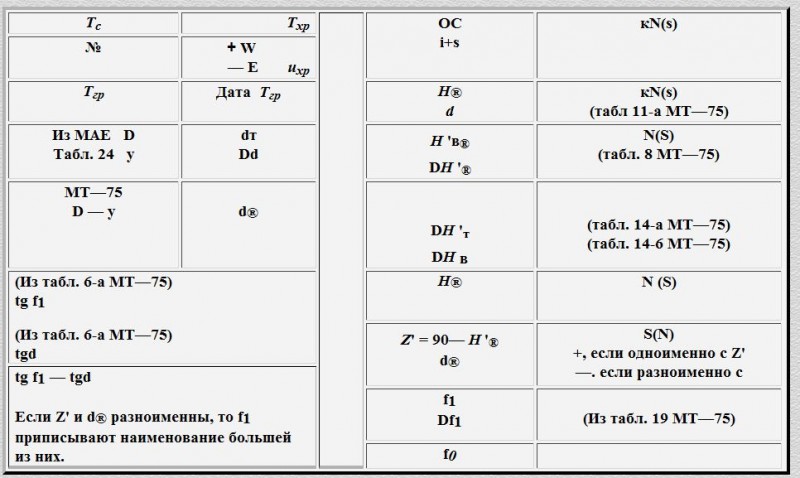
За меридиональную высоту Солнца H обычно принимают наибольшую из измеренных высот Hl , и широту f рассчитывают по формуле
Вследствие изменения склонения наблюдаемого светила и широты места при движении судна светило в момент наибольшей высоты находится вне меридиана наблюдателя, и поэтому рассчитанную широту требуется исправить поправкой
Df= ((D — y)/21.7)2 (tgf1+ tgd)
где D — часовое изменение склонения d в минутах дуги выбирается из МАЕ, причем D положительно, если светило приближается к повышенному полюсу, и отрицательно, если удаляется от него; y — часовое изменение широты в минутах (y=VcosПУ), y; положительно, если РШ одноименна с широтой, и
отрицательно, если РШ разноименна с широтой (y можно выбрать из табл. 24 МТ—75 как РШ за плавание данным курсом в течение часа)
Определив D и f, находят их разность.
Затем из таблицы 6-а МТ—75 выбирают tgf1, tgd и определяют их разность.
Из табл. 19 МТ—75 по найденным разностям D — y и tgf — tgd выбирают значение Df.
Наибольшая высота наблюдается до кульминации, если Солнце позади траверза судна, и после кульминации, если Солнце впереди траверза.
Поскольку опережение (отставание) может превышать 20 мин, это надо учитывать при выходе на наблюдения.
Определение широты по меридиональной высоте Солнца
В широтах до 50°, если изменение широты за 1 ч не превышает 12′, можно принимать f1 за f0.
Для определения времени выхода на наблюдения рассчитывают Тс кульминации Солнца по схеме:
Определение времени выхода на наблюдения рассчитывают Тс кульминации Солнца
Определение долготы по высоте светила на первом вертикале (А =90°)
Часовые углы в этой формуле считаем к W;
tгр — выбираем из МАЕ по замеченному времени наблюдения;
tм — местный часовой угол рассчитываем по измеренной высоте, склонению из МАЕ и счислимой широте по формуле
cos t =sin h sec f sec d — tg f tg d,
которую для упрощения вычислении преобразуем в вид
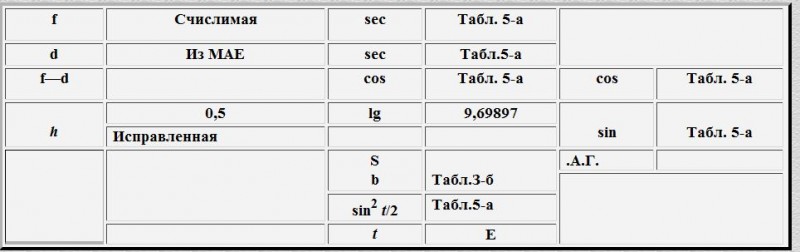
lg sin2 t/2 = lg 0,5 + lg secf + lg sec d + lg cos (f—d) +b,
где b— вспомогательный логарифм. Его выбираем из таблиц логарифмов разностей b (табл. З-б МТ-75) по аргументу Гаусса (А. Г. lg cos ((f—d) — lg sin h).
1) исправляем высоту и рассчитываем tгр и d по МАЕ;
2) рассчитываем местный часовой угол.
Определение долготы по высоте светила на первом вертикале
Переводим восточный часовой угол в западный tw =360° — tE.
Рассчитываем долготу lE = tw — tгр.
Если lE > 180°, переводим в lw = 360° —lE .
Так как азимут светила при измерении высоты был 90°, то полученная долгота практически свободна от ошибок из-за неточности широты
Определение поправки компаса
где А — азимут светила в круговом счете (для определения А используются табл. 20-а и 20-6 МТ-75); КП — компасный пеленг на светило.
Способ определения поправки компаса путем пеленгования верхнего края Солнца в моменты его восхода или захода является приближенным, особенно в высоких широтах, вследствие неустойчивой астрономической рефракции при малых высотах Солнца.
При пеленговании светил с высотой более 30° ошибки быстро возрастают Следует избегать применения откидного зеркала пеленгатора и критически относиться к поправке компаса, если при пеленговании использовали зеркало.
Необходимо следить, чтобы пеленгатор не имел наклона относительно плоскости вертикала светила. Замечать отсчет пеленга следует только после нескольких предварительных прицеливании. Для устранения промахов следует пеленговать светило сериями из трех-пяти измерений пеленгов и моментов с последующим осреднением результатов.
Для вычислений пользуются таблицами ТИПС*, ВАС** или ТВА***, в которых приведены правила их использования.
измеряем три-пять пеленгов светила, замечая моменты Тхр с точностью до 10 с;
замечаем судовое время Tc , отсчет лага ол и КК, снимаем с карты fc и lc;
рассчитываем средний Тхр;
определяем Тгр и находим по МАЕ tм и d светила;
по fc , d и tм рассчитываем по таблицам азимут светила;
рассчитываем средний КП и находим DК.
В частном случае поправку компаса DК определяют по пеленгу на Полярную звезду. Порядок действий описан в пояснении к МАЕ, с помощью которого делаются все вычисления, кроме исправления высоты. Расчеты местного часового угла Полярной звезды можно вести с точностью до 0,1°.
Источник
Наземное солнечное излучение
В то время, как солнечное излучение, падающее на земную атмосферу относительно постоянно, излучение, доходящее до поверхности Земли подвержено существенным вариациям.
Освещенность поверхности Земли зависит от:
— атмосферных явлений, таких как поглощение и рассеяние
— локальных изменений в составе атмосферы, как, например, наличие водяного пара, облаков или загрязнений
— широты места
— времени года и дня
Вышеперечисленные факторы влияют на общий поток энергии излучения, его спектральный состав, а также угол, под которым свет падает на поверхность. Главным следствием наличия атмосферы является то, что солнечное излучение на поверхности Земли значительно изменяется в зависимости от местоположения. Эти изменения обусловленны как локальными эффектами (облака, сезонные изменения), так и другими эффектами, такими как продолжительность светового дня на определенной широте. В пустынной местности солнечное излучение более постоянно вследствие отсутствия облаков, в экваториальных регионах — из-за меньших сезонных изменений положения относительно Солнца.
Солнечное излучение на поверхности Земли отличается от солнечного излучения, падающего на земную атмосферу. Это обусловлено наличием облачного покрова, загрязнителей воздуха, широтой местоположения и временем года.
— уменьшение плотности потока солнечного излучения в следствие поглащения, рассеяния и отражения в атмосфере
— изменение спектрального состава солнечного излучения в следствие различного поглащения и рассеяния различных длинн волн
— появление диффузной или не прямой составляющей в солнечном излучении
— локальные изменения атмосферы (такие как концентрация водяного пара, облака, загрязнения), которые оказывают дополнительное влияние на мощность, спектр и напраление падающего излучения.
Поглощение в атмосфере
Поглощение атмосферными газами изменяет спектральный состав наземного солнечного излучения, в то же время они практически не оказывают влияния на общую плотность потока излучения. Главным фактором, уменьшающим плотность потока излучения, является поглощение и рассеяние света на молекулах воздуха и частицах пыли. Следствием молекулярного поглощения являются не отдельные глубокие минимумы в спектре излучения, а уменьшение спектральной плотности потока излучения, зависящее от пути, проходимого через атмосферу. Когда Солнце находится в зените, молекулярное поглощение приводит к относительно равномерному уменьшению плотности потока по всему спектру, и свет кажется белым. Однако, для более длинных расстояний, проходимых светом, коротковолновое излучение поглощается и рассеивается сильнее. Поэтому утром и вечером Солнце кажется более красным, а свет не таким ярким, как в полдень.
Солнечное излучение вне земной атмосферы в сравнении с излучением, достигающим поверхности Земли. Человеческий глаз эволюционировал таким образом, чтобы иметь наибольшую чувствительность к излучению с наибольшей интенсивностью (Sekuler).
Прямое и диффузное излучение, возникающее в результате рассеяния
Рассеяние не происходит в единственном направлении и поэтому кажется, что свет приходит со всех частей неба. Такой свет называется диффузным или рассеянным. Так как рассеянию подвегаются в основном синие волны, небо нам кажется синим. Если бы рассеяние не существовало небо казалось бы нам черным, а Солнце — просто диском. В ясный солнечный день рассеивается около 10% всего падающего солнечного излучения.
Влияние облаков и других локальных изменений в атмосфере
Выходной ток фотоэлектрической батареи в солнечный и пасмурный дни зимой в Мельбурне. Батарея расположена под углом 60 0 (Mack).
где θ — это угол, отсчитываемый от вертикали (зенитный угол). Когда Солнце находится прямо над головой, θ = 90 и атмосферная масса равна 1.
Атмосферная масса представляет собой отношение атмосферного пути, проходимого светом, к кротчайшему из этих возможных путей, и равняется Y/X.
Например, угол, отсчитываемый от вертикали,θ= 30°
Атмосферная масса, AM = 1.1547 единиц
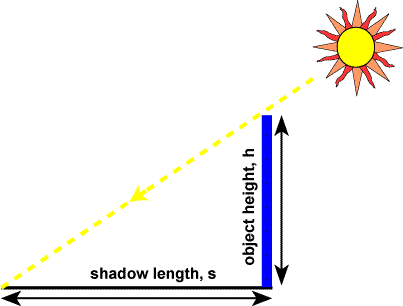
Для определения атмосферной массы существует простой метод, в котором используется длина тени, отбрасываемой вертикальным шестом.
Атмосферная масса равна длине гипотенузы, разделенной на длину шеста и по теореме Пифагора:
Например, высота объекта, h = 1 единиц
Длина тени, s = 1 единиц
Атмосферная масса, AM = 1.4142 единиц
В этой задаче предполагается, что атмосфера — это плоский горизонтальный слой. Но на самом деле это не так. Кривизна атмосферы приводит к тому, что, когда Солнце близко к горизонту, атмосферная масса отличается от длины атмосферного пути. На восходе угол Солнца, отсчитываемый от вертикали, равен 90 и атмосферная масса должна быть равной бесконечности, тогда как очевидно, что длина атмосферного пути конечна. Следующее уравнение учитывает кривизну шарообразность Земли:
Стандартный солнечный спектр и солнечное излучение
Стандартный спектр вне земной атмосферы называется АМ0, потому что свет не проходит через атмосферу. Обычно этот спектр используют для расчета эффективности солнечных элементов для космических аппаратов.
Расчет интенсивности излучения на основе атмосферной массы
где It — это интенсивность на площадке, перпендикулярной солнечным лучам в кВт/м2, АМ — атмосферная масса. 1.353 кВт/м2 — это солнечная постоянная, а 0.7 учитывает тот факт, что около 70% солнечного излучения, приходящего на границу атмосферы, достигает земли. Показатель 0.678 — эмпирический коэффициент, учитывающее неоднородность атмосферных слоев.
Интенсивность солнечного излучения увеличивается при увеличении высоты над уровнем моря. Спектральный состав солнечного света так же меняется, что делает свет более синим высоко в горах. Для высот в пределах нескольких километров над уровнем моря можно использовать простое приближение, умножив значение для поверхности Земли на (1-0.14h), где h — это высота над уровнем моря.
Диффузное излучени даже при ясном небе составляет около 10% прямого. Поэтому в ясный день общая интенсивность излучения, падающего на модуль, ориентированный перпендикулярно солнечным лучам, равна:
Например, атмосферная масса, AM = 1.5 единиц
Интенсивность прямого излучения,
Приблизительная общая интенсивность , IG = 0.9306 кВт/м2.
Движение солнца по небу сильно влияет на количество энергии, получаемой солнечным элементом. Освещенность поверхности и плотность потока падающего излучения равны, если излучение падает под прямым углом. При изменении угла между Солнцем и поглощающей поверхностью освещенность поверхности уменьшается. Когда солнечные лучи падают параллельно модулю и угол к нормали составляет 90 освещенность падает до нуля. Для других значений углов падения относительная интенсивность излучения равняется cosθ, где θ — это угол между солнечными лучами и нормалью к модулю.
Вы можете наблюдать, как изменяется интенсивность света при изменении наклона модуля с помощью рисунка ниже. В этом примере можно изменять наклон модуля, но то же самое происходит и при изменении угла, под которым падает солнечное излучение.
Угол между Солнцем и определенным местоположением на Земле зависит от координаты этого места (долготы), времени года и дня. Кроме этого от долготы местоположения зависит время восхода и захода Солнца. Поэтому, чтобы рассчитать угол падения солнечных лучей, нужно знать широту, долготу, день года и время дня. Об этом в следующих главах.
Солнечное время
Местное солнечное время и местное время
Время главного меридиана (долгота = 0) называется средним временем по Гринвичу. Местный стандартный временной меридиан обозначает местную временную зону. На рисунке показан LSTM временной зоны, включающей часть Бразилии и Гренландии.
LSTM рассчитывается с помощью формулы
где ΔTGMT — разница между местным временем и средним временем по Гринвичу в часах. 15°= 360°/24 часов.
в градусах и d — число дней с начала года. Поправка, определяемая уравнением времени, приведена на графике ниже:
Временной поправочный коэффициент
Множитель, равный четырем минутам учитывает то, что Земля поворачивается на 10 каждые 4 минуты.
Местное солнечное время (LST)
Рисунок показывает как изменяется угол наклона начиная с летнего солнцестояния в северном полушарии (зимнего в южном) до зимнего солнцестояния в северном полушарии (летнего в южном).
Склонение Солнца — это угол между экватором и воображаемой линией, соединяющей центры Земли и Солнца. Несмотря на то, что на самом деле Земля вращается вокруг Солнца, удобнее считать наоборот: что Солнце вращается вокруг неподвижной Земли. Для осуществления расчетов необходимо перейти в другую систему координат, в которой Солнце будет вращаться вокруг Земли.
Склонение можно посчитать по формуле (Cooper):
где d — день года (1 января = 1).
Более точное уравнение записывается так:
Склонение равно нулю в дни равноденствий (22 марта и 22 сентября), положительно, когда в северном полушарии лето и отрицательно, когда там зима. Максимума, равного 23.45° склонение достигает 22 июня (летнее солнцестояние в северном полушарии) и минимума, −23.45°, 22 декабря (зимнее солнцестояние в северном полушарии).
Угол возвышения изменяется в течение дня. Он также зависит от широты местоположения и времени года.
При проектировании фотоэлектрической системы важно знать максимальный угол возвышения для данной местности, то есть максимальную высоту Солнца на небе в определенное время года. Солнце достигает максимальной высоты в полдень по солнечному времени и эта высота зависит от угла склонения и широты, как показано на изображении ниже:
Максимальный угол возвышения в солнечный полдень (a) зависит от широты и угла склонения (δ).
Из рисунка можно получить угол возвышения в солнечный полдень для северного полушария:
и для южного полушария:
где φ — это широта местоположения. В уравнении для северного полушария широта положительна в местоположениях на северном полушарии и отрицательна в южном полушарии. В уравнении для южного полушария широта положительна для местоположений на южном полушарии и отрицательна на северном. φ — это угол склонения, зависящий от времени года.
В районе северного тропика в день осеннего солнцестояния Солнце находится прямо над головой и угол возвышения равен 90°. Летом на широтах между экватором и северным тропиком угол возвышения в солнечный полдень превышает 90°, учитывая то, что Солнце движется скорее с севера, чем с юга, как на большей части северного полушария. Аналогично, на широтах между экватором и южным тропиком в определенные периоды года солнечный свет приходит скорее с юга, чем с севера.
Более тщательное проектирование фотоэлектрических систем требует наличие данных не только о максимально угле возвышения, но о его изменении в течении всего дня. Уравнения, описывающие это изменения приведены на следующей странице.
Угол возвышения можно найти по следующей формуле:
Зенитный гол — это угол между Солнцем и вертикалью.
Восход и заход Солнца
Полярный угол отсчитывается аналогично показаниям компаса: он равен 00 на севере и 1800 на юге. Иногда используют другие начала отсчета, например с 00 на юге и полярным углом изменяющимся в интервале −180° до 180° .
Полярный угол можно рассчитать, зная параметры, введенные ранее:
Это уравнение справедливо только для полярных углов в течении солнечного утра, поэтому
Azimuth = Azi, для LST 12 или HRA >0
Время главного меридиана (долгота = 0) называется средним временем по Гринвичу. Местный стандартный временной меридиан обозначает местную временную зону. Это LSTM временной зоны, включающей часть Бразилии и Гренландии.
LSTM рассчитывается с помощью формулы
где ΔTGMT — разница между местным временем и средним временем по Гринвичу в часах. 15°= 360°/24 часов.
Уравнение времени (EoT)
в градусах и d — число дней с начала года. Поправка, определяемая уравнением времени, приведена на графике ниже:
В солнечных часах уравнение времени используется в виде таблицы. С его помощью устанавливается точное время для любого времени года. Другие поправочные коэффициенты либо учитываются при конструкции солнечных часов, либо вводятся с помощью констант.
Временной поправочный коэффициент (TC)
Множитель, равный четырем минутам, возникает из-за того, что Земля поворачивается на 10 каждые 4 минуты.
Местное солнечное время (LST)
Часовой угол (HRA)
где d — день года (1 января = 1).
Угол возвышения и полярный угол
График справа показывает значение полярного угла Солнца и угла возвышения, спроецированные на плоскость. Угол возвышения, равный 900, соответствует тому моменту, когда Солнце находится в зените и появляется в центре графика. Угол возвышения, равный 00, соответствует моменту, когда Солнце находится на горизонте и появляется на внешнем круге графика. Полярные углы отмечены вдоль окружности, ноль находится на самом верху. Посмотрите, как выглядит график для различных значений местоположения и времени. Тогда он станет более понятным.
Объяснение полярных координат
Положение Солнца с высокой точностью
Для модулей, которые следят за положением Солнца и концентрируют свет, неточность, обусловленная упрощением уравнений, неприемлима. Чем больше концентрация, тем выше необходимость в точности слеженя за Солнцем. Для систем, которые усиливают интенсивность света в 1000 раз точность должна достигать 3.5 минут (0.06°) окружности (Vant-Hull). Существует множество алгоритмов расчета положения Солнца. Более сложные модели дают более точные результаты, однако требуют больших вычислительных ресурсов. Если раньше простоте вычислений уделяли много вринмания, то сегодня даже маленькие микроконтроллеры могут справиться со сложными математическими формулами. Также положения Солнца можно опредилить по таблицам Астрономического Календаря, который составляется Военноморской Обсерваторией США (Astronomical Almanac).
В 2001г. Blanco-Muriel, работающий в Plataforma Solar de Almerýa (PSA) изучил точность всех алгоритмов. Позже они разработали упрощенный алгоритм расчета, который дает результат с точностью до 0.5 минут окружности для Этот алгоритм был специально оптимизирован для языка C++. Калькулятор положения Солнца, прведенный ниже, использует алгоритм, разработанный в PSA.
Алгоритм PSA для определеиня положения Солнца с высокой точностью
Значения, установленные по умолчанию, определяют полдень 1ого января 2008 года на долготе 0° (восточная Африка). Полярный угол равный 178° говорит о том, что Солнце находится почти на юге. Зенитный угол показывает, что Солнце находится высоко в небе, но на 23° ниже, чем при самом высоком положении.
Год — 2012 Месяц — 8 День — 22 Время по Гринвичу.
Час — 12 Минута — 00 Секунда — 00
Долгота = 0 Широта = 0
Полярный угол = 3.3888градусов
Склонение градусов = 11.5649
Угол возвышения градусов = 11.5649
Солнечное излучение на наклонной поверхности
Наклон модуля по отношению к падающему свету уменьшает его производительность.
Рисунок показывает расчет различных освещений. В каждом случае длина вектора дает относительную интенсивность излучения.
Уравнения, связывающие Smodule, Shoriz и Sincident:
где α — угол возвышения, β — угол наклона модуля
Ранее мы получили угол возвышения, как
где φ — широта, а δ — угол солнечного склонения:
где d — день в году.
Из этих уравнений можно получить зависимость между Smodule и Shoriz:
Следующий калькулятор, зная только одну составляющую излучения, рассчитывает все остальные.
Угол наклона имеет значительное влияние на солнечное излучение, падающее на поверхность. Если угол наклона неизменен, то максимальная производительность за весь года достигается тогда, когда он равен широте местоположения. Более пологие углы наклона способствуют увеличению падающего излучения летом, тогда как более крутые — зимой. Интерактивный график ниже рассчитывает и показывает максимальную плотность энергии излучения в течении дня в зависимости от широты и угла наклона модуля.
Влияние широты и угла наклона модуля на получаемое солнечное излучение в течении года в Втчас/м2день при условии отсутствия облаков. По оси х дни отсчитываются с первого января. Освещеность модуля — это солнечное излучение, падающее на наклонный модуль. Угол наклона модуля измеряется от горизонтали.
Падающая плотность потока излучения — это солнечное излучение, перпендикулярное модулю. Такое количество энергии получил бы модуль, очень точно поворачивающийся за Солнцем. Горизонтальная плотность потока излучения — это солнечное излучение, которое падает на землю, и которое получал бы модуль просто лежащий на земле. Эти значения нужно рассматривать, как максимально возможные для определенного местоположения, потому что при расчете не учитывался облачный покров. Предполагалось, что модуль ориентирован на юг в северном полушарии и на север в южном. Для некоторых углов свет падет с задней стороны модуля и поэтому поверхностная плотность излучения равна нулю.
Как можно видеть из графика, при нулевом угле наклона поверхностная плотность излучения на модуле равна горизонтальной поверхностной плотности излучения, так как модуль лежит на земле. Если угол наклона равен 800, то модуль практически вертикален и поверхностная плотность излучения модуля меньше, чем падающая поверхностная плотность излучения, кроме тех моментов, когда модуль перпендикулярен солнечным лучам и их значения равны. Модуль ориентирован по отношению к экватору так, что в южном полушарии он развернут на север, а в северном — на юг. При переходе модуля из северного в южное полушарии (на широте 00) он разворачивается в противоположную сторону, поэтому кривая претерпевает скачек. Установите широту вашего местоположения и, изменяя угол наклона, вы можете наблюдать, как будет меняться количество энергии, получаемое модулем в течении года.
Произвольная ориентация и угол наклона
где α — угол возвышения солнца, Θ — полярный угол солнца, β — угол наклона модуля. Если модуль просто лежит на земле, то β = 0°, если поставлен вертикально, то β = 90°. Ψ — полярный угол, на который повернут модуль. Абсолютное большинство модулей ориентированы в сторону экватора. Модуль в южном полушарии будет обращен на север с Ψ = 0°, а модуль в северном полушарии обычно прямо на юг с Ψ = 180°. Smodule и Sincident — поверхностные плотности излучения модуля и падающего света в Вт/м2, при чем Sincident — это только прямая составляющая излучения ( не учитывает рассеянное).
Если модуль обращен к Солнцу так, что солнечные лучи падают перпендикулярно его поверхности, то угол его наклона равен полярному углу Солнца (90 — α = β), а углы склонения Солнца и модуля равны между собой (Ψ = Θ).
В расчете, приведенном ниже, вычисление положения Солнца объединено с формулой для атмосферной массы. И в результате получается интенсивность света, падающего на модуль с произвольным углом наклона и ориентацией.
Время по Гринвичу (не местное)
Год — 2004 Месяц — 1 День — 1 Час — 22 Минута — 0 Секунда — 0
Долгота = 151 Широта = -34
Полярный угол модуля= 0° Наклон модуля= 34°
Полярный угол Солнца = 94.7078° Возвышение = 53.0242° Склонение = 36.9758° (по формуле PSA)
Атмосферная масса единиц = 1.6626(по формуле атмосферной массы )
Sincident = 0.8178 Вт/м² (по формуле интенсивности для атмосферной массы)
0.462 = уменьшение интенсивности излучения, падающего на модуль
Smodule = 0.3778 Вт/м² интенсивность излучения, падающего на модуль
Использование векторов для вычисления направления на Солнце
Свет, падающий на поверхность под углом занимает большую площадь, чем свет, падающий перпендикулярно. Уменьшение интенсивности равно скалярному произведению S на N.
где S — единичный вектор, направленный на Солнце, а N — единичный вектор, нормальный к поверхности модуля. γ — угол между двумя векторами.
Источник