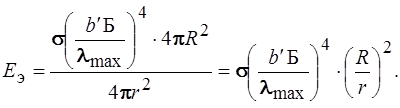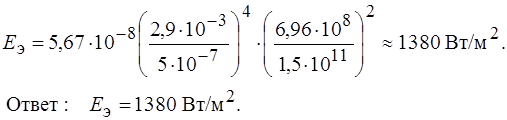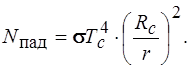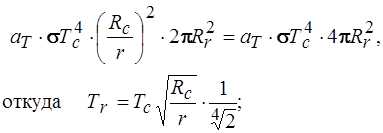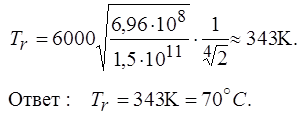Примеры решения задач. Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм
Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм. Определить энергетическую освещенность поверхности Земли, принимая Солнце за абсолютно черное тело.
| Дано: lmax = 0,5 мкм = 5 × 10 –7 м rc = 6,96 × 10 8 м r = 1,5 × 10 11 м s = 5,67×10 –8 Вт/(м 2 ×К 4 ) | Решение Энергетическая освещенность поверхности Земли равна потоку солнечной энергии, падающей на единицу поверхности Земли. Будем считать Солнце сферой, площадь поверхности которой |
| Еэ – ? | S = 4 p rc 2 . |
Поток энергии, излучаемой Солнцем,
Фс = Rэ × 4 p R 2 ,
где Rэ = s . T 4 c, так как, по условию задачи, Солнце – абсолютно черное тело.
Фс = s . T 4 c × 4 p R 2 .
Температуру поверхности Солнца Тс определим из закона Вина
Тс = b΄/ lmax .
Поток солнечной энергии распространяется от Солнца по всем направлениям в пределах 4p радиан (в дальнейшем будем считать Солнце точечным источником). На единицу любой поверхности находящейся на расстоянии r от Солнца, приходится энергия, равная Фс / (4p . r 2 ) .
Задача 16. Внутри солнечной системы на том же расстоянии от Солнца, как и Земля, находится частица сферической формы. Полагая Солнце абсолютно черным телом с температурой Тс = 6000 К и что температура частицы во всех ее точках одинакова, определить ее температуру, считая частицу серым телом.
| Дано: r = 1,5 . 10 11 м Тс = 6000 К Rс = 6,96 . 10 8 м l= 500 нм | Решение Частица – серое тело, следовательно, ее поглощательная способность одинакова для всех длин волн и при данной температуре частиц аl,Т = аT . Так как температура частицы постоянна во всех ее точках, соблюдается условие равновесия: |
| Тr – ? | мощность излучения, поглощаемого частицей, равна |
мощности излучения, испускаемой ею
Определим Nпогл, исходя из объяснения решения предыдущей задачи. Мощность солнечного излучения, падающего на единицу поверхности частицы, равна
Если учесть, что к Солнцу обращена половина поверхности частицы, то на поверхность частицы падает мощность солнечного излучения, равная
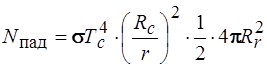
где Rc – радиус частицы.
Частица – это серое тело, поэтому она поглощает не всю энергию, а только часть ее.
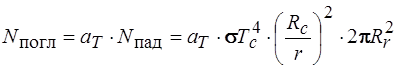
Определим энергию, излучаемую частицей
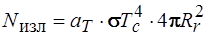
Приравнивая правые части последних соотношений, получим
Задача 17. Определить, за какое время зачерненный металлический шар диаметром D остынет с температуры T1 до температуры T2. Теплоемкость шара С. Остывание идет только за счет теплового излучения.
Теплоемкость твердого тела определяется формулой
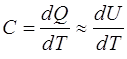
где dU – это изменение внутренней энергии, так как при нагревании происходит незначительное изменение объема тела.
Вследствие теплового излучения происходит убыль внутренней энергии шара, равная d U = – C d T .
С другой стороны, энергия, излучаемая нагретым шаром за время dt, равна dE = s T 4 × 4p R 2 ×d t .
Приравнивая правые части последних соотношений, получим
– C d T = s T 4 × 4p R 2 ×d t.
Проводим разделение переменных и решаем полученные интегралы
Источник
Электронная библиотека
Пример 1. Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны l = 0,48 мкм. Считая, что Солнце излучает как черное тело, определить: 1) температуру его поверхности; 2) мощность, излучаемую его поверхностью.
Решение. Согласно закону смещения Вина, искомая температура поверхности Солнца , где b = 2,9 10 -3 м ×К – постоянная Вина.
Мощность, излучаемая поверхностью Солнца, равна:
где – энергетическая светимость черного тела (Солнца); – площадь поверхности Солнца. Согласно закону Стефана-Больцмана, , где = 5,67 10 -8 Вт/(м 2 К 4 ) – постоянная Стефана-Больцмана.
Подставив записанные выражения в формулу (1), найдем искомую мощность, излучаемую поверхностью Солнца:
Вычисляя, получим: 1) = 6040 К, 2) = 4,58 10 26 Вт.
Пример 2. Натрий освещается монохроматическим светом с длиной волны = 40 нм. Определить наименьшее задерживающее напряжение ( ), при котором фототок прекратится.
«Красная граница» фотоэффекта для натрия = 584 нм.
Решение. Задерживающее напряжение можно определить из выражения:
где е = 1,6×10 -16 Кл – заряд электрона. Кинетическую энергию электрона определим из уравнения Эйнштейна:
где А – работа выхода;
Подставив формулу (3) в (2), получим:
Подставив формулу (4) в (1), найдем искомое задерживающее напряжение:
Вычисляя, получим: = 28,9 В.
Пример 3. Определить максимальное изменение длины волны при комптоновском рассеянии света на свободных электронах.
Решение. Для определения максимального изменения длины волны воспользуемся формулой Комптона:
где — изменение длины волны фотона в результате рассеяния на свободном электроне; h – постоянная Планка, m0 – масса покоя электрона; с— скорость света в вакууме; θ – угол рассеяния фотона, для определения максимальной длины волны угол рассеяния равен 180 градусов, тогда получим:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Источник
Максимум спектральной плотности энергетической светимости поверхности солнца
Задача 539. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Пример 2. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Мe Солнца; 2) поток энергии Фe, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.

Задачи для самостоятельного решения:
1. Определить, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость ослабла в 16 раз.
2. Температура внутренней поверхности муфельной печи при при открытом отверстии площадью равна Т. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая мощность составляет Р.
3. Определить, как и во сколько раз изменится излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с л1 до л2
4. Площадь, ограниченная графиком спектральной плотности энергетической светимости r(л,Т) черного тела, при переходе от термодинамической температуры Т1 к температуре Т2 увеличилась в 5 раз. Определить, как изменится при этом длина волны лmax, соответствующая максимуму спектральной плотности энергетической светимости черного тела.
5. В результате нагревания черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, сместилось с л1, до л2. Определить, во сколько раз увеличилась: 1). энергетическая светимость тела; 2). максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного тела возрастает по закону (r(л,Т))max=СТ^5, где С извесная постоянная величина.
6. Определить, какая длина волны соответствует максимальной спектральной плотност энергетической светимости (r(л,Т))max (С – постояннай в законе, связывающем максимальную спектральную плостность энергетической чветимости черного тела с термодинамической температурой и равна 1,3*10^(-5) Вт(м^3*K^5). 7. Считая никель черным телом, определите мощность, необходимую для поддержания температуры расплавленного никеля t неизменной, если площадь его поверхности равна S. Потерями пренебречь
8. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответстует длина волны л, определить: 1). температуру поверхности Солнца; 2). энергию, излучаемую Солнцем в виде электромагнитных волн за время t; 3) массу, теряемую Солнцем за это время за счёт излучения.
9. Определить темепратуру тела, при которой оно при температуре окружающей среды t0 излучало энергии в n раз больше чем поглощало.
10. Считая, что тепловые потери обусловлены только излучением, опеределите, какую мощность необходимо подводить к медному шарику диаметром d, чтобы при температуре окружающей среды t0 поддерживать его температуру равной t. Примите поглощательную способность меди Аr.
11. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d, температура которой в вакууме поддердивается постоянной и равной t. Поверхность проволоки считать серой с поглощательной способностью Ar. Удельное сопротивление проволоки при данной температуре ро. Температура окружающей проволоку среды t0
12. Используя формулу Планка, определите спектральную плотность потока излучения еденицы поверхности черного тела, приходящегося на узкий интервал длин волн дл около максимума спектральной плотности энергетической светимости, если температура черного тела T.
13. Для вольфрамовой нити при температуре T поглощательная способность Ar. Определить радиационную температуру нити.
14. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U0.
Источник
$ AlexLat $
По определению поверхностная плотность потока излучения, падающего на данную поверхность, то есть энергетическая освещенность Ее определяется по формуле
Ee=dФе/dS,
где dФe — поток солнечной энергии излучения, падающий на элемент сферической поверхности dS.
В силу равномерности излучения Солнца по всем направлениям величина освещенности Ее будет во всех точках сферы радиуса r одинакова.
Это позволяет определить необходимую мощность излучения Солнца Фе, приходящуюся на всю поверхность сферы r
Фе =Ее ⋅ S,
где r — расстояние от Солнца до Земли.
С другой стороны, эта мощность определяется согласно закону сохранения энергии мощностью теплового излучения Солнца как абсолютно черного тела, имеющего форму сферы радиуса rС. Мощность теплового излучения Солнца ФеС — определяется произведением энергетической светимости М 0 еС и площади поверхности Солнца
ФеС = Ме⋅SС,
где SС = 4π rС 2 , rС — радиус Солнца.
Мощность излучения постоянна
ФеС = Фе.
Откуда, с учетом выражения для мощности излучения найдем искомую величину Еe
Eе = Mе (rС/r) 2
Энергетическая светимость абсолютно черного тела определяется на основании закона Стефана-Больцмана (1.8)
Me = σT 4 c
где Тc — температура поверхности Солнца, σ = 5,67⋅10 -8 Вт/(м 2 ⋅К 4 ), а температура излучения — по заданной длине волны, на которую приходится максимум спектральной плотности энергетической светимости, из закона Tc = b/λm, b = 2,9⋅10 -3 м⋅К.
Расчетная формула для искомой величины плотности потока излучения вблизи Земли в итоге такова
Ee = σ (b/λm) 4 (rc/r)2=1,4,кВт/м 2
Источник
Будь умным!
Работа добавлена на сайт samzan.ru: 2016-03-30
» xml:lang=»ru-RU» lang=»ru-RU»>4. Примеры решения задач
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 1. » xml:lang=»ru-RU» lang=»ru-RU»> Максимум спектральной плотности энергетической светимости Солнца приходится на длину волны =0,48 мкм. Считая, что Солнце излучает как черное тело, определить: 1) температуру его поверхности; 2) мощность, излучаемую его поверхностью.
» xml:lang=»ru-RU» lang=»ru-RU»>Согласно закону смещения Вина, искомая температура поверхности Солнца:
» xml:lang=»ru-RU» lang=»ru-RU»> , (1)
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>b » xml:lang=»ru-RU» lang=»ru-RU»>= — постоянная Вина.
» xml:lang=»ru-RU» lang=»ru-RU»>Мощность, излучаемая поверхностью Солнца:
» xml:lang=»ru-RU» lang=»ru-RU»> , (2)
» xml:lang=»ru-RU» lang=»ru-RU»>где — энергетическая светимость черного тела (Солнца), — площадь поверхности Солнца, — радиус Солнца.
» xml:lang=»ru-RU» lang=»ru-RU»>Согласно закону Стефана — Больцмана:
» xml:lang=»ru-RU» lang=»ru-RU»> , (3)
» xml:lang=»ru-RU» lang=»ru-RU»>где = Вт/ — постоянная Стефана — Больцмана.
» xml:lang=»ru-RU» lang=»ru-RU»>Подставим записанные выражения в формулу (2), найдем искомую мощность, излучаемую поверхностью Солнца:
» xml:lang=»ru-RU» lang=»ru-RU»> . (4)
» xml:lang=»ru-RU» lang=»ru-RU»>Вычисляя, получим: Т=6,04 кК; Р=Вт.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 2. » xml:lang=»ru-RU» lang=»ru-RU»>Определить длину волны , массу и импульс фотона с энергией = 1 МэВ.
» xml:lang=»ru-RU» lang=»ru-RU»>Энергия фотона связана с дли- ной волны света соотношением: ,
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>h » xml:lang=»ru-RU» lang=»ru-RU»> постоянная Планка, с скорость света в вакууме. Отсюда .
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив численные значения, получим: м.
» xml:lang=»ru-RU» lang=»ru-RU»>Массу фотона определим, используя формулу Эйнштейна . Масса фотона = кг.
» xml:lang=»ru-RU» lang=»ru-RU»>Импульс фотона = кг м/с.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 3. » xml:lang=»ru-RU» lang=»ru-RU»> Натриевый катод вакуумного фотоэлемента освещается монохроматическим светом с длиной волны =40 нм. Определить задерживающее напряжение, при котором фототок прекращается. «Красная граница» фотоэффекта для натрия =584 нм.
» xml:lang=»ru-RU» lang=»ru-RU»>Электрическое поле, препят- ствующее движению электронов от катода к аноду, называют обратным. Напряжение, при котором фототок полностью прекращается, называется задерживающим напряжением. При таком задерживающем напряжении ни один из электронов, даже обладающий при вылете из катода максимальной скоростью , не может преодолеть задерживающего поля и достигнуть анода. При этом начальная кинетическая энергия фотоэлектронов () переходит в потенциальную (, где е=Кл элементарный заряд, а — наименьшее задерживающее напряжение). По закону сохранения энергии
» xml:lang=»ru-RU» lang=»ru-RU»> = . (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Кинетическую энергию электронов найдем, используя уравнение Эйнштейна для внешнего фотоэффекта:
» xml:lang=»ru-RU» lang=»ru-RU»>. (2)
» xml:lang=»ru-RU» lang=»ru-RU»>Отсюда (3)
» xml:lang=»ru-RU» lang=»ru-RU»>Работа выхода электронов А ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>в » xml:lang=»ru-RU» lang=»ru-RU»> определяется красной границей фотоэффекта:
» xml:lang=»ru-RU» lang=»ru-RU»>. (4)
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив выражение (4) в уравнение (3), получим:
» xml:lang=»ru-RU» lang=»ru-RU»>Тогда, из уравнения (1) .
» xml:lang=»ru-RU» lang=»ru-RU»>Вычисляя, получим В.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 4. » xml:lang=»ru-RU» lang=»ru-RU»>Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить длину волны де Бройля для протона.
» xml:lang=»ru-RU» lang=»ru-RU»>Длина волны де Бройля определяется по формуле: , (1)
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>h » xml:lang=»ru-RU» lang=»ru-RU»> постоянная Планка, — импульс частицы.
» xml:lang=»ru-RU» lang=»ru-RU»>По условию задачи кинетическая энергия протона сравнима по величине с его энергией покоя Е ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>0 » xml:lang=»ru-RU» lang=»ru-RU»>. Следовательно, импульс и кинетическая энергия связаны между собой релятивистским соотношением:
» xml:lang=»ru-RU» lang=»ru-RU»> , (2)
» xml:lang=»ru-RU» lang=»ru-RU»>где с скорость света в вакууме.
» xml:lang=»ru-RU» lang=»ru-RU»>Используя условие задачи, получим: . Подставив полученное выражение в формулу (1), найдем длину волны де Бройля:
» xml:lang=»ru-RU» lang=»ru-RU»>Энергию покоя электрона найдем по формуле Эйнштейна , где » xml:lang=»en-US» lang=»en-US»>m ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>0 » xml:lang=»ru-RU» lang=»ru-RU»> — масса покоя электрона, с — скорость света в вакууме.
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив числовые значения, получим: м.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 5. » xml:lang=»ru-RU» lang=»ru-RU»> Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов » xml:lang=»en-US» lang=»en-US»>U » xml:lang=»ru-RU» lang=»ru-RU»>=0,5 кВ. Принимая, что неопределенность импульса электрона равна 0,1 % от его числового значения, определить неопределенность координаты электрона. Является ли в данных условиях электрон квантовой или классической частицей?
» xml:lang=»ru-RU» lang=»ru-RU»> Решение
» xml:lang=»ru-RU» lang=»ru-RU»> В направлении движения пучка электронов (ось » xml:lang=»en-US» lang=»en-US»>X » xml:lang=»ru-RU» lang=»ru-RU»>) соотношение неопределенностей имеет вид:
» xml:lang=»ru-RU» lang=»ru-RU»> , (1)
» xml:lang=»ru-RU» lang=»ru-RU»>где — неопределенность координаты электрона; — неопределенность его импульса; — постоянная Планка.
» xml:lang=»ru-RU» lang=»ru-RU»>Пройдя ускоряющую разность потенциалов, электрон приобретает кинетическую энергию , равную работе сил электрического поля:
» xml:lang=»ru-RU» lang=»ru-RU»>Расчет дает значение Е ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>к » xml:lang=»ru-RU» lang=»ru-RU»>=500 эВ, что много меньше энергии покоя электрона (Е ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>0 » xml:lang=»ru-RU» lang=»ru-RU»> = 0,51 Мэв). Следовательно, в данных условиях электрон является нерелятивистской частицей, имеющей импульс, связанный с кинетической энергией формулой .
» xml:lang=»ru-RU» lang=»ru-RU»>Согласно условию задачи, неопределенность импульса =0,001 = , т.е.
» xml:lang=»ru-RU» lang=»ru-RU»>Это значит, что волновые свойства в данных условиях несущественны и электрон может рассматриваться как классическая частица. Из выражения (1) следует, что искомая неопределенность координаты электрона
» xml:lang=»ru-RU» lang=»ru-RU»>Вычислив, получим 8,51 нм.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 6. » xml:lang=»ru-RU» lang=»ru-RU»> В результате перехода из одного стационарного состояния в другое атомом водорода был испущен квант с частотой . Найти, как изменились радиус орбиты и скорость движения электрона, используя теорию Бора.
» xml:lang=»ru-RU» lang=»ru-RU»>Излучение с частотой соответствует длине волны = =102,6 нм (с скорость света в вакууме), лежащей в ультрафиолетовой области. Следовательно, спектральная линия принадлежит серии Лаймана, возникающей при переходе электрона на первый энергетический уровень ( » xml:lang=»en-US» lang=»en-US»>n » xml:lang=»ru-RU» lang=»ru-RU»>=1).
» xml:lang=»ru-RU» lang=»ru-RU»>Используем обобщенную формулу Бальмера, чтобы определить номер энергетического уровня ( » xml:lang=»en-US» lang=»en-US»>k » xml:lang=»ru-RU» lang=»ru-RU»>), с которого был совершен переход: .
» xml:lang=»ru-RU» lang=»ru-RU»>Выразим из этой формулы » xml:lang=»en-US» lang=»en-US»>k » xml:lang=»ru-RU» lang=»ru-RU»>:
» xml:lang=»ru-RU» lang=»ru-RU»>Подставляя имеющиеся данные, получим » xml:lang=»en-US» lang=»en-US»>k » xml:lang=»ru-RU» lang=»ru-RU»>=3. Следовательно, излучение произошло в результате перехода электрона с третьей орбиты на первую.
» xml:lang=»ru-RU» lang=»ru-RU»>Значения радиусов орбит и скоростей движения электронов на этих орбитах найдем из следующих соображений.
» xml:lang=»ru-RU» lang=»ru-RU»>На электрон, находящийся на стационарной орбите в атоме водорода, со стороны ядра действует сила Кулона
» xml:lang=»ru-RU» lang=»ru-RU»>которая сообщает ему нормальное ускорение . Следовательно, согласно основному закону динамики:
» xml:lang=»ru-RU» lang=»ru-RU»>. (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Кроме того, согласно постулату Бора, момент импульса электрона на стационарной орбите должен быть кратен постоянной Планка, т.е.
» xml:lang=»ru-RU» lang=»ru-RU»> , (2)
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>n » xml:lang=»ru-RU» lang=»ru-RU»> = 1, 2, 3 …. номер стационарной орбиты.
» xml:lang=»ru-RU» lang=»ru-RU»>Из уравнения (2) скорость . Подставив это выражение в уравнение (1), получим
» xml:lang=»ru-RU» lang=»ru-RU»> Отсюда радиус стационарной орбиты электрона в атоме водорода: .
» xml:lang=»ru-RU» lang=»ru-RU»>Тогда скорость электрона на этой орбите:
» xml:lang=»ru-RU» lang=»ru-RU»>Принимая, что до излучения кванта электрон имел характеристики » xml:lang=»en-US» lang=»en-US»>r ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>3 » xml:lang=»ru-RU» lang=»ru-RU»>, » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>3 » xml:lang=»ru-RU» lang=»ru-RU»>, а после излучения » xml:lang=»en-US» lang=»en-US»>r ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>1 » xml:lang=»ru-RU» lang=»ru-RU»>, » xml:lang=»en-US» lang=»en-US»>v ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>1 » xml:lang=»ru-RU» lang=»ru-RU»> несложно получить:
» xml:lang=»ru-RU» lang=»ru-RU»>то есть, радиус орбиты уменьшился в 9 раз, скорость электрона увеличилась в 3 раза.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 7. » xml:lang=»ru-RU» lang=»ru-RU»> Электрон в одномерной прямоугольной «потенциальной яме» шириной =200 пм с бесконечно высокими «стенками» находится в возбужденном состоянии ( » xml:lang=»en-US» lang=»en-US»>n » xml:lang=»ru-RU» lang=»ru-RU»>=2). Определить: 1) вероятность » xml:lang=»en-US» lang=»en-US»>W » xml:lang=»ru-RU» lang=»ru-RU»> обнаружения электрона в средней трети «ямы»; 2) точки указанного интервала, в которых плотность вероятности обнаружения электрона максимальна и минимальна.
» xml:lang=»ru-RU» lang=»ru-RU»> Решение
» xml:lang=»ru-RU» lang=»ru-RU»>1. Вероятность обнаружить частицу в интервале » xml:lang=»en-US» lang=»en-US»>x » xml:lang=»ru-RU» lang=»ru-RU»>
» xml:lang=»ru-RU» lang=»ru-RU»> . (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Возбужденному состоянию ( » xml:lang=»en-US» lang=»en-US»>n » xml:lang=»ru-RU» lang=»ru-RU»>=2) отвечает собственная волновая функция:
» xml:lang=»ru-RU» lang=»ru-RU»> . (2)
» xml:lang=»ru-RU» lang=»ru-RU»>Подставим (2) в (1) и учтем, что и :
» xml:lang=»ru-RU» lang=»ru-RU»>Выразив через косинус двойного угла с использованием тригонометрического равенства , получим выражение для искомой вероятности: = == = = 0,195.
» xml:lang=»ru-RU» lang=»ru-RU»>2. Плотность вероятности существования частицы в некоторой области пространства определяется квадратом модуля ее волновой функции . Используя выражение (2), получим:
» xml:lang=»ru-RU» lang=»ru-RU»> . (3)
» xml:lang=»ru-RU» lang=»ru-RU»>Зависимость квадрата модуля волновой функции частицы от ее координаты, определяемая выражением (3), приведена на рисунке.
» xml:lang=»ru-RU» lang=»ru-RU»>Очевидно, что минимальная плотность вероятности » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»>=0 соответствует значениям » xml:lang=»en-US» lang=»en-US»>x » xml:lang=»ru-RU» lang=»ru-RU»>, при которых .
» xml:lang=»ru-RU» lang=»ru-RU»>То есть, ,
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>k » xml:lang=»ru-RU» lang=»ru-RU»> = 0, 1, 2…
» xml:lang=»ru-RU» lang=»ru-RU»>Максимального значения в пределах ямы плотность вероятности » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»> достигает при условии: . Соответствующие значения .
» xml:lang=»ru-RU» lang=»ru-RU»>Как видно из графика зависимости » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»>= » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»>( » xml:lang=»en-US» lang=»en-US»>x » xml:lang=»ru-RU» lang=»ru-RU»>), приведенного на рисунке, в интервал » xml:lang=»en-US» lang=»en-US»>x » xml:lang=»ru-RU» lang=»ru-RU»> » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»> достигает максимального значения на границах интервала при или . Найдем значения » xml:lang=»en-US» lang=»en-US»>w » xml:lang=»ru-RU» lang=»ru-RU»> на границах указанного интервала, используя выражение (3):
» xml:lang=»ru-RU» lang=»ru-RU»>Как видим, плотность вероятности обнаружить электрон на границах заданного интервала — одинакова. Следовательно, , .
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 8. » xml:lang=»ru-RU» lang=»ru-RU»>Определить количество теплоты, необходимое для нагревания кристалла » xml:lang=»en-US» lang=»en-US»>NaCl » xml:lang=»ru-RU» lang=»ru-RU»> массой » xml:lang=»en-US» lang=»en-US»>m » xml:lang=»ru-RU» lang=»ru-RU»>=20г на от температуры Т ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>1 » xml:lang=»ru-RU» lang=»ru-RU»> = 2К. Характеристическую температуру Дебая для » xml:lang=»en-US» lang=»en-US»>NaCl » xml:lang=»ru-RU» lang=»ru-RU»> принять равной 320К..
» xml:lang=»ru-RU» lang=»ru-RU»>Количество теплоты, необходимое для нагревания тела массой » xml:lang=»en-US» lang=»en-US»>m » xml:lang=»ru-RU» lang=»ru-RU»> от температуры Т ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>1 » xml:lang=»ru-RU» lang=»ru-RU»> до температуры Т ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>2 » xml:lang=»ru-RU» lang=»ru-RU»> можно вычислить по формуле:
» xml:lang=»ru-RU» lang=»ru-RU»>, (1)
» xml:lang=»ru-RU» lang=»ru-RU»>где С молярная теплоемкость вещества, М молярная масса.
» xml:lang=»ru-RU» lang=»ru-RU»>Согласно теории Дебая, при температуре молярная теплоемкость кристаллических твердых тел определяется выражением:
» xml:lang=»ru-RU» lang=»ru-RU»>. (2)
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив выражение (2) в (1), и проинтегрировав, получим:
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив численные значения и произведя вычисления, найдем » xml:lang=»en-US» lang=»en-US»>Q » xml:lang=»ru-RU» lang=»ru-RU»>= 1,22 мДж.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 9. » xml:lang=»ru-RU» lang=»ru-RU»> Вычислить дефект массы, энергию связи и удельную энергию связи ядра .
» xml:lang=»ru-RU» lang=»ru-RU»> Решение
» xml:lang=»ru-RU» lang=»ru-RU»>Дефект массы ядра определим по формуле:
» xml:lang=»ru-RU» lang=»ru-RU»> . (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Для ядра : » xml:lang=»en-US» lang=»en-US»>Z » xml:lang=»ru-RU» lang=»ru-RU»>=5; А=11.
» xml:lang=»ru-RU» lang=»ru-RU»> Вычисление дефекта массы выполним во внесистемных единицах атомных еди- ницах массы (а.е.м.). Необходимые данные возьмем из таблицы (приложение 3):
» xml:lang=»ru-RU» lang=»ru-RU»>=1,00783 а.е.м., =1,00867 а.е.м., = 11,00931 а.е.м.
» xml:lang=»ru-RU» lang=»ru-RU»>В результате расчета по формуле (1) получим: =0,08186 а.е.м.
» xml:lang=»ru-RU» lang=»ru-RU»>Энергию связи ядра найдем также во внесистемных единицах (МэВ), воспользовавшись формулой:
» xml:lang=»ru-RU» lang=»ru-RU»> . (2)
» xml:lang=»ru-RU» lang=»ru-RU»>Коэффициент пропорциональности = 931,4 МэВ/а.е.м., т.е.
» xml:lang=»ru-RU» lang=»ru-RU»>После подстановки численных значений получим:
» xml:lang=»ru-RU» lang=»ru-RU»> 76,24 МэВ.
» xml:lang=»ru-RU» lang=»ru-RU»>Удельная энергия связи, по определению, равна:
» xml:lang=»ru-RU» lang=»ru-RU»>Примечание. » xml:lang=»ru-RU» lang=»ru-RU»>Расчет дефекта массы ядра должен проводиться с максимально возможной точностью, т.е. с учетом всех значащих цифр, указанных в табличных данных.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 10. » xml:lang=»ru-RU» lang=»ru-RU»> Определить период полураспада радиоактивного изотопа, если известно, что за 1 сутки из 1 млн ядер распадается 175 тысяч.
» xml:lang=»ru-RU» lang=»ru-RU»>Период полураспада связан с постоянной радиоактивного распада соот- ношением:
» xml:lang=»ru-RU» lang=»ru-RU»> . (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Постоянную радиоактивного распада найдем, используя закон радиоактивного распада:
» xml:lang=»ru-RU» lang=»ru-RU»> , (2)
» xml:lang=»ru-RU» lang=»ru-RU»>где » xml:lang=»en-US» lang=»en-US»>N » xml:lang=»ru-RU» lang=»ru-RU»> число ядер, не распавшихся к моменту времени » xml:lang=»en-US» lang=»en-US»>t » xml:lang=»ru-RU» lang=»ru-RU»>, — начальное число ядер.
» xml:lang=»ru-RU» lang=»ru-RU»>Разделив уравнение (2) на и прологарифмировав обе части, получим:
» xml:lang=»ru-RU» lang=»ru-RU»> или .
» xml:lang=»ru-RU» lang=»ru-RU»>Учет того, что » xml:lang=»en-US» lang=»en-US»>N » xml:lang=»ru-RU» lang=»ru-RU»>=- , дает:
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив это выражение в (1), получим для периода полураспада следующее выражение:
» xml:lang=»ru-RU» lang=»ru-RU»>Подстановка численных значений и расчет приводят к результату с.
» xml:lang=»ru-RU» lang=»ru-RU»>Примечание. » xml:lang=»ru-RU» lang=»ru-RU»> Решая задачи подобного типа, допускается использование внесистемных единиц измерения времени, таких как — час, сутки, год.
» xml:lang=»ru-RU» lang=»ru-RU»>Пример 11. » xml:lang=»ru-RU» lang=»ru-RU»> При соударении — частицы с ядром бора произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер оказалось ядро атома водорода . Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
» xml:lang=»ru-RU» lang=»ru-RU»> Решение
» xml:lang=»ru-RU» lang=»ru-RU»>Обозначим неизвестное ядро символом .
» xml:lang=»ru-RU» lang=»ru-RU»>Так как — частица представляет собой ядро гелия , запись
» xml:lang=»ru-RU» lang=»ru-RU»>реакции будет иметь вид:
» xml:lang=»ru-RU» lang=»ru-RU»>Применив закон сохранения массового числа, получим:
» xml:lang=»ru-RU» lang=»ru-RU»>отсюда А=13.
» xml:lang=»ru-RU» lang=»ru-RU»>Применив закон сохранения зарядового числа, получим:
» xml:lang=»ru-RU» lang=»ru-RU»>2+5=1+ » xml:lang=»en-US» lang=»en-US»>Z » xml:lang=»ru-RU» lang=»ru-RU»>,
» xml:lang=»ru-RU» lang=»ru-RU»>отсюда » xml:lang=»en-US» lang=»en-US»>Z » xml:lang=»ru-RU» lang=»ru-RU»>=6.
» xml:lang=»ru-RU» lang=»ru-RU»>По периодической системе элементов найдем, что неизвестное ядро является ядром изотопа углерода .
» xml:lang=»ru-RU» lang=»ru-RU»>В окончательном виде реакцию можно записать так:
» xml:lang=»ru-RU» lang=»ru-RU»>Определим энергию реакции (энергетический эффект) по формуле:
» xml:lang=»ru-RU» lang=»ru-RU»> . (1)
» xml:lang=»ru-RU» lang=»ru-RU»>Заменив массы ядер массами нейтральных атомов, получим:
» xml:lang=»ru-RU» lang=»ru-RU»>где — масса электрона.
» xml:lang=»ru-RU» lang=»ru-RU»>Упростив уравнение (2), получим:
» xml:lang=»ru-RU» lang=»ru-RU»> . (3)
» xml:lang=»ru-RU» lang=»ru-RU»>Массы атомов найдем в таблице приложения 3 :
» xml:lang=»ru-RU» lang=»ru-RU»>=10,01294 а.е.м., =4,00260 а.е.м.,
» xml:lang=»ru-RU» lang=»ru-RU»>=1,00783 а.е.м., =13,00335 а.е.м.
» xml:lang=»ru-RU» lang=»ru-RU»>Подставив в (3) массы атомов в а.е.м., а с учетом того, что коэффициент пропорциональности =931,4 МэВ/а.е.м., получим:
» xml:lang=»en-US» lang=»en-US»>Q » xml:lang=»ru-RU» lang=»ru-RU»>=4,06 МэВ.
» xml:lang=»ru-RU» lang=»ru-RU»>Реакция идет с выделением тепла, т.е. является экзотермической.
» xml:lang=»ru-RU» lang=»ru-RU»>
Дано: СИ:
= » xml:lang=»ru-RU» lang=»ru-RU»>0,48 мкм » xml:lang=»ru-RU» lang=»ru-RU»>м
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ:
» xml:lang=»ru-RU» lang=»ru-RU»>=40 нм м
» xml:lang=»ru-RU» lang=»ru-RU»>=584 нм м
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ:
» xml:lang=»en-US» lang=»en-US»>U » xml:lang=»ru-RU» lang=»ru-RU»>=0,5 кВ 500 В
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ:
» xml:lang=»en-US» lang=»en-US»>t » xml:lang=»ru-RU» lang=»ru-RU»>=1 сут с
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: » xml:lang=»en-US» lang=»en-US»>
» xml:lang=»en-US» lang=»en-US»>Z — ? A — ? X — ? Q — ?
» xml:lang=»ru-RU» lang=»ru-RU»>Е ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>к » xml:lang=»ru-RU» lang=»ru-RU»>=Е ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>0 » xml:lang=»en-US» lang=»en-US»>/4
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ
» xml:lang=»en-US» lang=»en-US»>m » xml:lang=»ru-RU» lang=»ru-RU»>=20г 0,02кг
» xml:lang=»ru-RU» lang=»ru-RU»>Т ;vertical-align:sub» xml:lang=»ru-RU» lang=»ru-RU»>1 » xml:lang=»ru-RU» lang=»ru-RU»>=10К
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ:
» xml:lang=»ru-RU» lang=»ru-RU»>= 1МэВ Дж
» xml:lang=»en-US» lang=»en-US»>m » xml:lang=»ru-RU» lang=»ru-RU»> — ?
» xml:lang=»en-US» lang=»en-US»>p » xml:lang=»ru-RU» lang=»ru-RU»> — ?
» xml:lang=»ru-RU» lang=»ru-RU»>Дано: СИ:
» xml:lang=»ru-RU» lang=»ru-RU»>=200 пм м
» xml:lang=»ru-RU» lang=»ru-RU»>1) » xml:lang=»en-US» lang=»en-US»>W » xml:lang=»ru-RU» lang=»ru-RU»> — ?
» xml:lang=»ru-RU» lang=»ru-RU»>2) » xml:lang=»en-US» lang=»en-US»>x ;vertical-align:sub» xml:lang=»en-US» lang=»en-US»>max » xml:lang=»en-US» lang=»en-US»> -?

Материалы собраны группой SamZan и находятся в свободном доступе
Источник