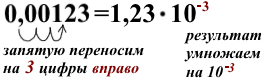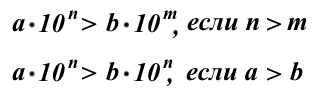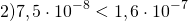Стандартный вид числа
Стандартный вид числа — это его запись в виде произведения
Число n называется порядком числа, записанного в стандартном виде.
В стандартном виде можно записать любое положительное число.
Как правило, стандартный вид числа используют для записи больших и малых величин.
Записать число в стандартном виде и указать порядок числа:
2) 12 346 000 000;
Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a 
Получили число, записанное в стандартном виде. Его порядок n=6.
При решении примеров на приведение числа к стандартному виду удобнее деление числа на
заменить умножением на
Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:
2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:
Это число записано в стандартном виде. Его порядок n=10.
Чтобы первый множитель соответствовал условию 1≤a 
Порядок числа n= -3.
Таким образом, для приведения к стандартному виду числа, меньшего единицы, запятую в его записи переносим на n цифр вправо и результат умножаем на 10 в степени -n:
Переносим запятую в записи числа на 5 цифр вправо (что соответствует умножению числа на 10⁵). Результат умножаем на 10 в минус пятой степени. Порядок числа n= -5.
Порядок числа n= -4.
Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.
Далее выполняем умножение степеней с одинаковыми основаниями.
Порядок числа n=6.
Порядок числа n=6.
Порядок числа n= -4.
Порядок числа n= -10.
Сравнение чисел, записанные в стандартном виде
- Сравниваем порядок чисел. Число с большим порядком больше числа с меньшим порядком.
- Если числа имеют одинаковые порядки, сравнивают первые множители произведения.
9,8 \cdot 10^7 \]» title=»Rendered by QuickLaTeX.com»/>
так как порядок первого числа больше порядка второго числа (8>7);
поскольку порядок первого числа меньше порядка второго числа (-8 
2,97 \cdot 10^9 \]» title=»Rendered by QuickLaTeX.com»/>
так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).
Источник
Cтандартный вид числа
В задачах по физике часто приходится работать с очень большими и очень малыми величинами.
Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?
Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.
Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число « 10 » в различных степенях.
- 10 − 2 =
1 10 2 =
1 100 = 0,01 (более подробно об отрицательной степени можно прочитать в уроке 9 класса «Отрицательная степень»)
- 10 −1 =
1 10 1 =
1 10 = 0,1
- 10 0 = 1
- 10 1 = 10
- 10 2 = 100
- 10 3 = 1000
- …
Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..
- 5 · 10 = 50
- 27 · 100 = 2 700
- 18 · 1000 = 18 000
Теперь запишем тоже самое, используя определение степени.
- 5 · 10 = 5 · 10 1 = 50
- 27 · 100 = 27 · 10 2 = 2 700
- 18 · 1000 = 18 · 10 3 = 18 000
При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.
- 13 000 : 100 =
13 000 100 = 130
- 50 : 10 =
50 10 = 5
Для десятичных дробей действует схожее правило умножения на 10, 100, 1000 . При умножении десятичной дроби на 10, 100, 1000 и т.д. мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д.
- 5,7 · 100 = 570
- 7,013 · 10 = 70,13
- 68,3 · 1000 = 68 300
С помощью степени можно записать вычисления выше следующим образом:
- 5,7 · 100 = 5,7 · 10 2 = 570
- 7,013 · 10 = 7,013 · 10 1 = 70,13
- 68,3 · 1000 = 68,3 · 10 3 = 68 300
При делении на 10, 100, 1000 и т.д. перемещаем запятую влево .
- 6,7 : 10 =
6,7 10 = 0,67
- 0,15 : 100 =
0,15 100 = 0,0015
С помощью определения отрицательной степени можно записать вычисления выше следующим образом:
- 6,7 : 10 =
6,7 10 = 6,7 · 10 −1 = 0,67
- 0,15 : 100 =
0,15 100 = 0,15 · 10 −2 = 0,0015
Стандартный вид числа
Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
Такая запись называется — стандартный вид числа.
При этом число « n » называют порядком числа « a ».
Из определения выше важно понять, что степень, в которой стоит « 10 », в стандартном виде числа называется порядком .
Теперь к примеру. Пусть нам дано число « 5 600 » и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
В числе « 5 600 » первая цифра справа — « 5 ». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.
Значит, чтобы из « 5 , 600 » получить « 5600 » нам нужно умножить « 5 , 600 » на « 1000 ». Запишем полученное преобразование.
Теперь запишем « 1000 » с использованием степени.
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
Таким образом « 5 600 » в стандартном виде будет выглядеть следующим образом:
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь « 0,017 ».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от « 1 » до « 9 ».
В десятичной дроби « 0,017 » вначале идет « 0 ». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от « 0 ».
Это цифра « 1 ». Посчитаем сколько знаков (цифр) стояло от запятой до цифры « 1 », включая саму цифру « 1 ».
Получается два знака. Начнем записывать « 0,017 » в стандартном виде. Перенесем запятую и поставим ее справа от « 1 ».
Ответим себе на вопрос: «На что нужно умножить или разделить « 1,7 », чтобы получить изначальное число « 0,017 » ?». Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится влево .
Выходит, чтобы из « 1,7 » сделать 0,017 », нужно « 1,7 разделить на « 100 » (чтобы перенести запятую на два знака влево).
Запишем это деление на « 100 », используя обыкновенную дробь.
С помощью отрицательной степени запишем окончательный вид числа « 0,017 » в стандартном виде.
0,017 = 1,7 : 100 = 1,7 ·
| 1 |
| 100 |
=
1,7 · 10 −2
Примеры решения задач
на запись числа в стандартном виде
№ 237 Алимов 8 класс
(Устно) Определить порядок числа, выражающего значение физической константы:
1) масса покоя электрона
me = 9,1093897 · 10 −31
Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень, в которой стоит « 10 ». В данном примере « 10 » стоит в
степени « −31 ». Значит, порядком массы покоя электрона является « −31 ».
№ 238 Алимов 8 класс
Записать в стандартном виде и определить порядок числа k , выражающего физического константу:
2) постоянная Фарадея
F = 96485,309 Кл/моль;
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра « 9 ».
Зададим себе вопрос: «На что нужно умножить « 9 , 6485309 », чтобы получить « 96485 , 309 » ?» Посчитаем количество знаков (цифр), на которое требуется перенести запятую в « 96485 , 309 », чтобы получить « 96485309 ».
Получается « 4 » знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:
Порядком числа « 9,6485309 · 10 4 » является степень, в которой стоит « 10 ». Следовательно, порядок « k = 4 ».
Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:
Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую, чтобы из « 2 , 686763 » получить « 2686763 ».
Значит, чтобы получить из « 2 , 686763 » нужно изначальное число « 2686763 » умножить на « 10 6 ».
Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».
Источник