Лазерная локация Луны. Отражение света от наклонного движущегося зеркала
Рис.1
Перейдём к световым единицам измерений. Положим св.ед.скорости = ед.скорости/ скорость света и тогда V→β. Мы знаем, что движущееся зеркало сокращается пропорционально коэффициенту Лоренца. Следовательно, угол α связан с углом α0 наклона зеркала в его собственной системе отсчёта формулой (1). На схеме рис.1 расстояние AC выражается формулой (2). Из (2) и (3) вычислим c∙t и y, и подставим в уравнение (4), откуда найдём значение x по формуле (6) и далее c∙t из (2). Затем вычислим tg δ по формуле (7). Из чертежа следует, что углы падения φ и отражения ψ связаны соотношением (8), которое и является решением задачи.
Уравнение (9) получено из мысленного эксперимента, заключающегося в том, что позиции источника света, зеркала и отражённого «зайчика» на экране, зафиксированные на лабораторном столе при его неподвижности, не должны измениться, когда он начнёт двигаться. Это следует из принципа относительности. Значения, вычисленные по формулам (8), удовлетворяют уравнению (9) при всех разумных сочетаниях углов падения, наклона зеркала и скорости. Естественно, при нулевом наклоне зеркала результаты совпадают с расчетами по формулам Болотовского и Столярова. 
Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
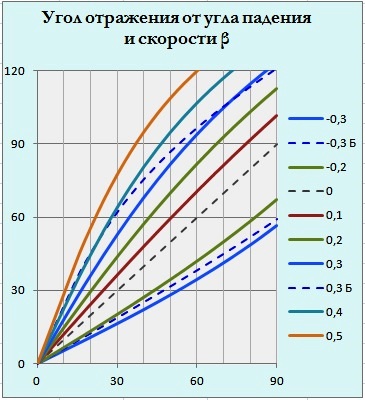
Графики приведены для диапазона скоростей зеркала от встречного движения -0,3 световой до +0,5 вдогонку.
Рис.2
Кстати, при отражении луча догоняющего зеркало, угол отражения может превышать 90°, как это отображено на рис.1. Для сравнения приведены графики отклонения для баллистической теории света отображённые синими пунктирными линиями для скоростей -0,3 и +0,3 световой и отмеченных литерой «Б». В этой теории свет считается частицами, а теория относительности отвергается. Расчёт проводился согласно школьной методике . Как видим, отклонения в таком случае будут иные, так что прямой эксперимент мог бы подтвердить или отвергнуть баллистическую теорию.
Итак, насколько же «зайчик» от уголкового отражателя на Луне отклонится от места установки лазера на Земле? Расчёты показывают, что максимальный угол отклонения, в точке верхней кульминации Луны, будет 0,0005 градуса. На Земле отклонение составит примерно 3,3 км в сторону движения Луны по орбите, но за 2,5 секунды, пока импульс возвратится, земная поверхность подъедет почти на километр, так что итоговое отклонение составит около 2,5 км. Поскольку размер отражённого лазерного зайчика на земной поверхности составляет порядка 15 км, заметить сам факт отклонения пока невозможно. И, кстати, отклонение по баллистической теории для этих условий совпадает с отклонением по СТО до 8-го знака (т.е. расхождение не более 10 метров).
Источник
Лазерная локация Луны. Отражение света от наклонного движущегося зеркала
Как известно, и мы, и американцы, установили на Луне уголковые отражатели, благодаря чему с помощью лазера можно измерять расстояние до неё с точностью до уже сантиметров.
Уголковый отражатель отражает падающий от излучателя луч строго в обратном направлении. Но это так, если излучатель и уголковый отражатель взаимно неподвижны. При локации Луны имеем, что Луна движется по орбите радиусом 380000 км со скоростью около 1,3 км/сек, и поверхность земли с излучателем и приёмником тоже движется, если я правильно понял, в ту же сторону со скоростью от 0,46 км/сек на экваторе до в два раза меньшего значения на 60-й широте.
Кроме того, законы отражения от движущегося зеркала отличаются для случаев, если свет волна и если свет частица. Насколько же промахивается отражённый от Луны луч и можно ли это заметить? Вычислим это, причём не выходя за рамки школьной математики. Автор будет благодарен за замечания и указания об ошибках.
Расчёт двойного отражения от движущихся зеркал уголкового отражателя не кажется простой задачей. Например, в статье Б.М.Болотовского и С.Н.Столярова «Отражение света от движущегося зеркала и родственные задачи» рассматривается только отражение от зеркала движущегося перпендикулярно своей поверхности путём пересчёта характеристик электромагнитных полей выражаемых уравнениями Максвелла. При этом обоснование метода излагается на 14 страницах.
Попробуем решить задачу для движущегося наклонного зеркала анализируя движение фронтов падающей и отражённой волн. Рассмотрим участок AO фронта волны шириной S. Луч (синие линии со стрелками) падает на зеркало (голубая линия) под углом φ от вектора скорости его движения V. Отражается он под углом ψ (зелёная дуга). Угол наклона нормали зеркала к вектору скорости равен α. Это конечно не полная 3D-схема, но для уголкового отражателя сгодится.
После попадания в зеркало края фронта AO волны в точке O, другой его край продолжает движение пока не попадёт в зеркало в точке C. На это потребуется время t и лучи, падающий и отражённый, пройдут расстояние c∙t, где с — скорость света. Следовательно, BO = AC. Это значит, что прямоугольные треугольники OAC, ODC и OBC равны.
Зеркало за это время сдвинется на расстояние V∙t, и часть расстояния до точки C добавится из-за наклона зеркала на угол α.
Рис.1
Перейдём к световым единицам измерений. Положим св.ед.скорости = ед.скорости/ скорость света и тогда V→β. Мы знаем, что движущееся зеркало сокращается пропорционально коэффициенту Лоренца. Следовательно, угол α связан с углом α0 наклона зеркала в его собственной системе отсчёта формулой (1). На схеме рис.1 расстояние AC выражается формулой (2). Из (2) и (3) вычислим c∙t и y, и подставим в уравнение (4), откуда найдём значение x по формуле (6) и далее c∙t из (2). Затем вычислим tg δ по формуле (7). Из чертежа следует, что углы падения φ и отражения ψ связаны соотношением (8), которое и является решением задачи.
Уравнение (9) получено из мысленного эксперимента, заключающегося в том, что позиции источника света, зеркала и отражённого «зайчика» на экране, зафиксированные на лабораторном столе при его неподвижности, не должны измениться, когда он начнёт двигаться. Это следует из принципа относительности. Значения, вычисленные по формулам (8), удовлетворяют уравнению (9) при всех разумных сочетаниях углов падения, наклона зеркала и скорости. Естественно, при нулевом наклоне зеркала результаты совпадают с расчетами по формулам Болотовского и Столярова.
Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
Графики приведены для диапазона скоростей зеркала от встречного движения -0,3 световой до +0,5 вдогонку.
Рис.2
Кстати, при отражении луча догоняющего зеркало, угол отражения может превышать 90°, как это отображено на рис.1. Для сравнения приведены графики отклонения для баллистической теории света отображённые синими пунктирными линиями для скоростей -0,3 и +0,3 световой и отмеченных литерой «Б». В этой теории свет считается частицами, а теория относительности отвергается. Расчёт проводился согласно школьной методике. Как видим, отклонения в таком случае будут иные, так что прямой эксперимент мог бы подтвердить или отвергнуть баллистическую теорию.
Итак, насколько же «зайчик» от уголкового отражателя на Луне отклонится от места установки лазера на Земле? Расчёты показывают, что максимальный угол отклонения, в точке верхней кульминации Луны, будет 0,0005 градуса. На Земле отклонение составит примерно 3,3 км в сторону движения Луны по орбите, но за 2,5 секунды, пока импульс возвратится, земная поверхность подъедет почти на километр, так что итоговое отклонение составит около 2,5 км. Поскольку размер отражённого лазерного зайчика на земной поверхности составляет порядка 15 км, заметить сам факт отклонения пока невозможно. И, кстати, отклонение по баллистической теории для этих условий совпадает с отклонением по СТО до 8-го знака (т.е. расхождение не более 10 метров).
Источник
Лунное отражение
Такая непривычная раскраска Луны получилась после совмещения двух изображений: на обычную фотографию Луны (полученную в оптическом диапазоне) наложено смоделированное излучение на длине волны 150 МГц, которое могла бы отражать в сторону Земли лунная поверхность, если бы она была идеально гладкой. Яркая желтая полоса — это синхротронное излучение электронов межзвездной среды в магнитном поле Млечного Пути. В этом диапазоне Луна отражает примерно 7% от попадающей на ее поверхность электромагнитной энергии. Отраженные радиоволны повышают «яркость» Луны на этой частоте примерно на 14%.
Стоит отметить, что если «посмотреть» на Луну в радиотелескоп на такой длине волны, то видна будет совсем не такая четкая картинка. Сигнал от отраженного синхротронного излучения будет сильно забит помехами: само оно будет рассеиваться на лунной поверхности, а еще довольно сильный эффект будет вносить отражение Луной радиоволн, имеющих земное происхождение (в частности, волн в диапазоне FM, в котором идет вещание большинства радиостанций).
Этот эффект больше всего известен по своей «оптической ипостаси», которая называется пепельным светом Луны: за несколько дней до новолуния и в течение нескольких дней после него, в то время, когда Луна есть на небе, а Солнца нет (например, сразу после заката), можно разгядеть полный лунный диск, который подсвечивается солнечным светом, отразившимся от поверхности Земли (подробнее об этом можно прочитать в картинке дня «Неомения и пепельный свет Луны»). Радиотелескопы позволяют непосредственно наблюдать отражение земных радиоволн от Луны.
Радиоволны (на частоте 68 МГц), имеющие земное происхождение, которые отражены лунной поверхностью обратно и зафиксированы радиоинтерферометром LOFAR. Слева вверху — полное изображение: Луна видна как темное пятно в центре, отраженный сигнал — яркое пятно в центре Луны, окружает это все фоновое излучение Млечного Пути. Цветом показана плотность потока излучения. Изображение из статьи H. K. Vedantham et al., 2015. Lunar occultation of the diffuse radio sky: LOFAR measurements between 35 and 80 MHz
Смоделированное отраженное излучение, которое было использовано на верхнем изображении, взято из недавней статьи с длинным названием Measuring the global 21-cm signal with the MWA-I: improved measurements of the Galactic synchrotron background using lunar occultation. Зачем же авторам этой работы понадобилось предсказывать изменение яркости Луны в радиодиапазоне, вызванное излучением, порожденным нашей Галактикой?
Дело тут в стремлении ученых разобраться с начальными этапами эволюции Вселенной. После рекомбинации (см. Recombination), когда из-за расширения и остывания Вселенной электроны и протоны смогли соединяться и образовывать атомы, Вселенная стала электронейтральной: практически ничего не излучало и не поглощало свет, из-за чего это время называют Темными веками (Dark ages, мельком об этом говорилось в задаче «Очень темные дела»). Постепенно огромные газовые облака, состоящие из водорода (и небольшого количества гелия), начали уплотняться и сжиматься под действием собственной гравитации — зажглись первые звезды, появились звездные скопления и галактики. Звезды излучали энергичные фотоны, которые стали вновь ионизировать межзвездный газ нашей Вселенной, — началась реионизация. Мы и сейчас живем во Вселенной, где большая часть газа в межзвездной и межгалактической среде находится в ионизированном состоянии.
Темные века таят очень много загадок. В частности, хотя общая картина происходившего примерно понятна, до сих пор остаются открытыми вопросы об образовании первых звезд и галактик, о появлении первых скоплений, сверхмассивных черных дыр и активных галактических ядер. Ответ на них следует искать именно в изучении сигналов, дошедших до нас из этой эпохи. Проблема в том, что нейтральный водород практически ничего не излучает и не поглощает, и это сильно затрудняет наблюдения.
Однако один очень полезный вид излучения всё же есть. Это излучение нейтрального водорода на длине волны 21 см (частота 1420 МГц), возникающее в атомарном водороде из-за «переворота» спина электрона относительно спина протона. С его помощью, в частности, в 60-е годы XX века удалось картографировать спиральные рукава Млечного Пути.
Карта Млечного Пути, составленная по итогам анализа излучения нейтрального водорода в 1959 году Яном Оортом. Изображение из статьи J. H. Oort, 1959. A summary and assessment of current 21-cm results concerning spiral and disk structures in our galaxy
Так почему же нельзя на этой длине волны увидеть излучение водорода, испущенное в Темные века? Дело в том, что из-за расширения Вселенной длина волны излучения, испущенного в какой-нибудь момент времени, постепенно увеличивается. Степень этого увеличения описывается параметром красного смещения \(z\) (выражающим относительное изменение длины волны \(\Delta \lambda/\lambda\)). Так, излучение горячего газа, которое было испущено еще до рекомбинации с длиной волны несколько микрон, мы видим сейчас как космический микроволновой фон на длине волны несколько миллиметров (так как красное смещение для такого излучения примерно равно 1100).
Так как для реионизации красное смещение составляет \(z\sim 10\), излучение, испущенное в те времена на длине волны 21 см, приходит к нам с длиной волны 210 см. С частотами происходит обратное: изначальная частота 1420 МГц превращается примерно в 142 МГц. Проблема в том, что на таких частотах очень сильно излучают электроны в магнитном поле нашей Галактики: они на 5–6 порядков ярче. Сложность этой задачи — поймать на таком фоне редкие фотоны, долетевшие до нас из молодой Вселенной, — сравнима с задачей услышать писк комара рядом с включенным двигателем реактивного самолета.
Чувствительность и точность (разрешающая способность) радиотелескопов пропорциональны размеру «собирающей» поверхности, однако содержать слишком большие телескопы тяжело и дорого, поэтому наблюдатели придумывают различные ухищрения, чтобы увеличивать точность, но не строить огромные «тарелки». Один из вариантов — использовать радиоинтерферометрию: несколько радиотелескопов в разных уголках Земли (и даже в космосе, см. Радиоастрон), работают вместе как один большой телескоп. Точность при этом примерно такая же, как была бы у гиганта с размерами, сравнимыми с расстоянием между телескопами. У интерферометров, правда, довольно плохая чувствительность.
В 1999 году было предложено использовать Луну для наблюдений на радиоинтерферометрах. Спутник Земли — отличная «мишень» для калибровки приборов, а из-за того, что Луна блокирует часть радиоизлучения неба, радиоинтерферометр становится чувствительным не к абсолютной яркости неба, а к разности яркости неба и Луны (в радиодиапазоне), что значительно повышает точность.
Но чтобы такой метод работал, нужно уметь предсказывать «радиояркость» Луны с очень хорошей точностью. Для этого ученые и выполняют моделирование, подобное тому, что показано на верхнем изображении.
Источник