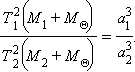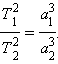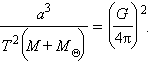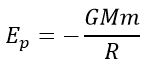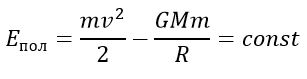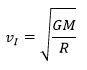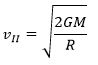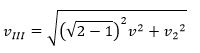Третий Закон Кеплера прочитать по новому
1. Третий закон Кеплера: Квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.
2. Если преобразовать известную формулу Кеплера, то получим формулу орбитального движения планеты :
R (в кубе) делить на T (в квадрате)
где также R — радиус орбиты (или полуосей эллипса)
T — период обращения планеты
Выяснилось, что для всех планет это отношения не меняется. Значение его зависит от того в каких единицах измеряем радиус и период..
3. В окончательном словесном выражении эта формула звучит так:
Для каждой планеты в общих единицах измерения отношение радиуса ее орбиты в кубе и ее периода в квадрате есть величина постоянная.
4.Частный случай третьего Закона Кеплера можно выразить в таком упрощенном виде:
Если радиус орбиты планеты выразить в астрономических единицах,а период в земных годах то тогда радиус в кубе равен периоду в квадрате.
3 2
R = T
4. есть еще одна вариация:
Произведение квадрата средних скоростей планет на средний радиус их орбит
(R x V x V ) , есть величина постоянная для всех планет Солнечной системы! (Проверено)
Эта формула удобна для вычислений и обязательны должна быть принята,но в физической природе нет квадрата скорости.
Эта формула математическая и речь в ней идет о расстоянии, пройденном за время.
Поэтому точнее написание формула для трехмерного пространства :
R S x S / t x t
где R радиус обриты планеты и S путь пройденный за определенное время t
7. Нам кажется,что формула третьего закона Кеплера есть производное из названного выше постулата о постоянстве для каждой планеты отношения куба радиуса орбиты и квадрата ее периода.
Третий закон Кеплера справедлив и для спутников планет.
Вероятно и для тел на орбите Земли.
8. Вероятно читателю будет интересно узнать о постоянстве такого соотношения основных параметров движения планет:
V х T / R
Соответственно: V скорость движения по орбите
T период обращения R радиус орбиты
проверка для некоторых планет V х T \ R :
Венера 35,02 х 0,615 : 0,7233 = 29,776
Земля. 29,783 х 1 : 1 = 29,783
Марс 24,13 х 1,88 :1,5236 = 29,77
Юпитер 13,07 х 11,86 : 5,204 = 29,78
Сатурн 9,66 х 29,46 : 9,54 = 29,83
Это значит,например, если мы знаем орбитальную скорость земли 29,783 км/сек
то чтобы узнать орбитальную скорость Марса нужно орбитальную скорость Земли 29,783 умножить на соотношение радиусов орбиты Марса и земли
1,523 и, разделив на соотношение периодов 1,88. получить орбитальную скорость Марса 24,13 км/сек
Источник
Квадраты периодов обращения планет вокруг солнца пропорциональны кубам больших
Три закона движения планет относительно Солнца были выведены эмпирически немецким астрономом Иоганном Кеплером в начале XVII века. Это стало возможным благодаря многолетним наблюдениям датского астронома Тихо Браге.
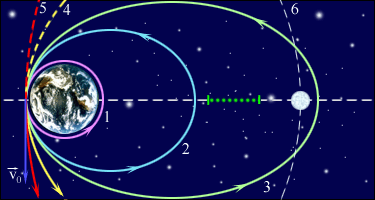
Первый закон Кеплера . Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
Второй закон Кеплера ( закон равных площадей ). Радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. Другая формулировка этого закона: секториальная скорость планеты постоянна.
Третий закон Кеплера . Квадраты периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.
Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.
В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам.
Скорость движения планеты в перигелии
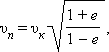 |
где к – средняя или круговая скорость планеты при = . Скорость движения в афелии
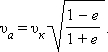 |
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения. Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.
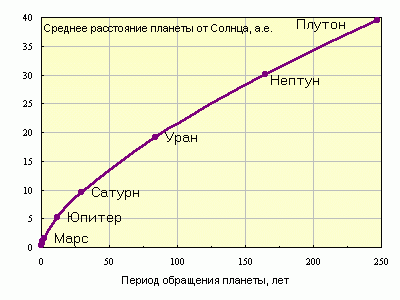 1 1 | ||||
| Рисунок 3.1.3.1. В обобщенном виде этот закон обычно формулируется так: квадраты периодов 1 и 2 обращения двух тел вокруг Солнца, помноженные на сумму масс каждого тела (соответственно 1 и 2) и Солнца
При этом взаимодействие между телами 1 и 2 не учитывается. Если пренебречь массами этих тел в сравнении с массой Солнца (т.е. 1 , 2 ), то получится формулировка третьего закона, данная самим Кеплером:
Третий закон Кеплера можно также выразить как зависимость между периодом обращения по орбите тела с массой и большой полуосью орбиты ( – гравитационная постоянная):
Здесь необходимо сделать следующее замечание. Для простоты часто говорится, что одно тело обращается вокруг другого, но это справедливо только для случая, когда масса первого тела пренебрежимо мала по сравнению с массой второго (притягивающего центра). Если же массы сравнимы, то следует учитывать и влияние менее массивного тела на более массивное. В системе координат с началом в центре масс орбиты обоих тел будут коническими сечениями, лежащими в одной плоскости и с фокусами в центре масс, с одинаковым эксцентриситетом. Различие будет только в линейных размерах орбит (если тела разной массы). В любой момент времени центр масс будет лежать на прямой, соединяющей центры тел, а расстояния до центра масс 1 и 2 тел массой 1 и 2 соответственно связаны следующим соотношением: 1/2 = 2/1. Перицентры и апоцентры своих орбит (если движение финитно) тела также будут проходить одновременно. Третий закон Кеплера можно использовать, чтобы определить массу двойных звезд. Источник Большая Энциклопедия Нефти и ГазаКвадрат — период — обращение — планетаКвадраты периодов обращения планет вокруг Солнца пропорциональны кубам соответствующих средних расстояний от Солнца. [1] Квадраты периодов обращения планет вокруг Солнца относятся как кубы их больших полуосей. [2] Квадраты периодов обращения планет вокруг Солнца пропорциональны кубам больших полуосей их орбит. [3] Квадраты периодов обращения планет вокруг Солнца пропорциональны кубам соответствующих средних расстояний планет от Солнца. [4] Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей их орбит. [5] Квадраты периодов обращения планет относятся, какжубы боль-щих полуосей их орбит. [6] Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. [7] Квадраты периодов обращения планет пропорциональны кубам их средних расстояний от Солнца. Или отношение R3IT2 одинаково для всех планет. [8] Квадраты периодов обращения планет вокруг Солнца пропорциональны кубам соответствующих средних расстояний планет от Солнца. [9] Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. [10] Квадраты периодов обращения планет относятся, как кубы больших полуосей их орбит. [11] Квадраты периодов обращения планет по эллипсам относятся как кубы больших полуосей. [12] Квадраты периодов обращения планет относятся, как кубы больших полуосей их орбит. [13] Отношение квадратов периодов обращения планет к кубам больших полуосей их орбит для всех планет одинаково. [14] Отношение куба большой полуоси планеты к произведению квадрата сидерического периода обращения планеты на сумму масс Солнца и планеты — есть величина постоянная. [15] Источник Потенциальная энергия взаимодействия двух телПусть два тела с массами M и m находятся на расстоянии R друг от друга. Тогда энергия их взаимодействия равна Полная энергияЕсли тело находится в гравитационном поле и имеет некоторую скорость, то его полная энергия равна Таким образом, в соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной. Теорема вириала В случае кругового движения кинетическая энергия в 2 раза меньше по модулю потенциальной. Поэтому Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела. При Eпол Система с отрицательной полной энергией называется гравитационно связанной . При Eпол = 0 тело движется по параболической траектории. Скорость тела на бесконечности равна нулю. При Eпол > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии. Первая космическая скоростьЭто скорость движения по круговой траектории вблизи поверхности Земли Это минимальная скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и стало спутником. Для Земли примерно 7,9 км/с. Вторая космическая скоростьЭто скорость движения по параболической траектории Она равна минимальной скорости, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца . Находится из условия равенства нулю полной энергии системы. Для Земли примерно 11,2 км/с. Третья космическая скоростьЭто скорость, при которой тело преодолевает притяжение Солнца где v – орбитальная скорость планеты, v 2 – вторая космическая скорость для планеты. Для Земли примерно 16,6 км/с. Задачи: Звезда и планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите массу планеты m, если известно, что скорость движения планеты равна v 1 , а скорость движения и период обращения звезды равны v 2 и T соответственно. Если бы все линейные размеры Солнечной системы были пропорционально сокращены так, чтобы среднее расстояние между Солнцем и Землей стало 1 м, то какова была бы продолжительность одного года? Считайте, что плотность небесных тел при этом не меняется. Автоматическая станция обращается вокруг планеты Марс с периодом T = 18 ч. Максимальное удаление от поверхности Марса (в апоцентре) a = 25000 км, минимальное (в перицентре) p = 1380 км. По указанным параметрам орбиты станции определите отношение массы Марса к массе Земли. Радиус Марса rм = 3400 км, радиус Земли rз = 6400 км. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты 422 тыс. км. Вычислить параболическую скорость на поверхности Луны, RЛ = 0.27 радиуса Земли, MЛ = 1/81 массы Земли. Источник Квадраты периодов обращения планет вокруг солнца пропорциональны кубам большихСовременная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола. В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам. Скорость движения планеты в перигелии где v c – средняя или круговая скорость планеты при r = a . Скорость движения в афелии Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения . Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел. Комета Галлея обращается вокруг Солнца с периодом обращения 76 лет. Нептун имеет период обращения 164,8 лет. Кто из них более удален от Солнца в точке афелия своей орбиты? аГ = 17,8 а.е., q = 0,59 а.е. Комета удаляется от Солнца на 2∙17,8 – 0,59 = 35,01 а.е. Большая полуось Нептуна а Нептуна = 30 а.е. Ответ. Дальше от Солнца в афелии находится комета Галлея. Комета Темпеля имеет вытянутую орбиту, ее перигелийное расстояние 1,37 а.е., период обращения вокруг Солнца Т = 5,26 лет. Найти наибольшее расстояние от Солнца, большую полуось и эксцентриситет кометы Темпеля. Большую полуось можно найти из третьего закона Кеплера T 2 / T 2 = a 3 / a 3 ; где Т = 1 год, а = 1 а.е. Наибольшее расстояние от Солнца – афелий орбиты кометы Q = 2 a – q = 4,63 а.е. Ответ. Эксцентриситет е = 0,54, афелий Q = 4,63 а.е., большая полуось а = 3,0 а.е. В XVIII веке была подмечена закономерность, которая в настоящее время называется правилом Тициуса–Боде. Средние расстояния от планет до Солнца выражаются, согласно этому правилу следующей формулой: а = 0,1∙(3∙2 n + 4) а.е. В 1993 году у пульсара PSR В 1257+12 были найдены три планеты. Все они находятся на расстояниях, пропорциональных (но не равных) расстояниям от Солнца Меркурия, Венеры и Земли (0,30/0,72/1,0). Что изменится в формулировке правила Тициуса – Боде для данной системы? Ответ. Коэффициент перед скобкой. Замечено, что противостояния некоторой малой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты? Понятие противостояния определено только для внешних планет: сидерический период Т = 2 года, а по третьему закону Кеплера T 2 / T 2 = a 2 / a 2 , отсюда большая полуось орбиты а = 1,59 а.е. Внешняя планета находится за орбитой Марса. Сколько времени нужно лететь с Земли на Марс по гомановской орбите в космическом корабле, перигелийное расстояние которого равно расстоянию от Земли до Солнца, а афелийное расстояние – расстоянию от Марса до Солнца? По третьему закону Кеплера большая полуось орбиты космического корабля Для Земли T = 1 год, a = 1 а.е., поэтому T = 1,4 года, а время полета Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 1 Какие небесные явления происходят при данных конфигурациях небесных тел: 1. Если А — планета Марс; В — Земля; С — Солнце, произойдет: 2. Если А — Земля; В — Солнце; С — планета Венера, произойдет: 3. В нижнем соединении не могут находиться … планеты: 1) внешние; 2) внутренние; 3) нижние планеты. 4. Рядом с Луной во время полнолуния могут быть видны … планеты: 1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать. 5. Максимальное угловое отклонение от Солнца наблюдается у: 1) Венеры; 2) Меркурия; 3) Марса. 6. Как меняется значение скорости движения кометы при ее перемещении от перигелия к афелию? 1) не изменяется; 2) увеличивается; 3) уменьшается; 4) скорость кометы не зависит от положения на орбите. 7. По каким траекториям движутся космические аппараты к Луне от Земли? 1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой. Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 2 Какие небесные явления происходят при данных конфигурациях небесных тел: 1. Если А — планета Юпитер; В — Земля; С — Солнце, произойдет: 2. Если А — Земля; В — Солнце; С — планета Меркурий, произойдет: 3. В нижнем соединении могут находиться … планеты: 1) внешние; 2) внутренние; 3) верхние планеты. 1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать. 5. Максимальное угловое отклонение от Солнца наблюдается у: 1) Венеры; 2) Меркурия; 3) Юпитера. 1) Чем дальше планета от Солнца, тем ее сидерический период больше. 2) Чем дальше планета от Солнца, тем ее сидерический период меньше. 3) Период обращения планет-гигантов не зависит от их расстояния до Солнца. 4) Период обращения планет-гигантов вокруг Солнца равен периоду их обращения вокруг оси. 7. По каким траекториям движутся космические аппараты к Луне от Земли? 1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой. Источник ➤ Adblockdetector |
 ) , относятся как кубы больших полуосей 1 и 2 их орбит:
) , относятся как кубы больших полуосей 1 и 2 их орбит: