Кто сформулировал законы движения планет вокруг солнца
Johannes Kepler, 1571–1630
Немецкий астроном. Родился в Вюртембурге. Начав с изучения богословия в Тюбингенской академии (позднее университет), увлекся математикой и астрономией и вскоре получил приглашение на должность преподавателя математики в гимназии австрийского города Грац. Там он снискал себе репутацию блестящего астролога благодаря ряду сбывшихся метеорологических прогнозов на 1595 год. Начиная с 1598 года Кеплер и другие протестанты стали подвергаться в католическом Граце жестоким религиозным гонениям, и в 1600 году ученый по приглашению датского астронома Тихо Браге переехал в Прагу. Работы Кеплера основывались на наблюдениях, сделанных Тихо Браге. Его дальнейшая жизнь сложилась трагично. Он жил в бедности и умер от лихорадки по дороге в Австрию, куда он отправился в надежде получить причитающееся ему жалованье.
Ч ем ближе планеты к Солнцу, тем больше линейная и угловая скорости их обращения вокруг Солнца. Период обращения планет вокруг Солнца по отношению к звездам называется звездным периодом.
Такой период обращения Земли относительно звезд называется звездным годом. Наименьший звездный период обращения у планеты Меркурий. У Марса он составляет около 2 лет, у Юпитера — 12 лет и, все возрастая с удалением от Солнца, у Плутона доходит до 250 лет.
Заслуга открытия законов движения планет принадлежит выдающемуся австрийскому ученому Кеплеру. В начале XVII в. Кеплер установил три закона движения планет. Они названы законами Кеплера.
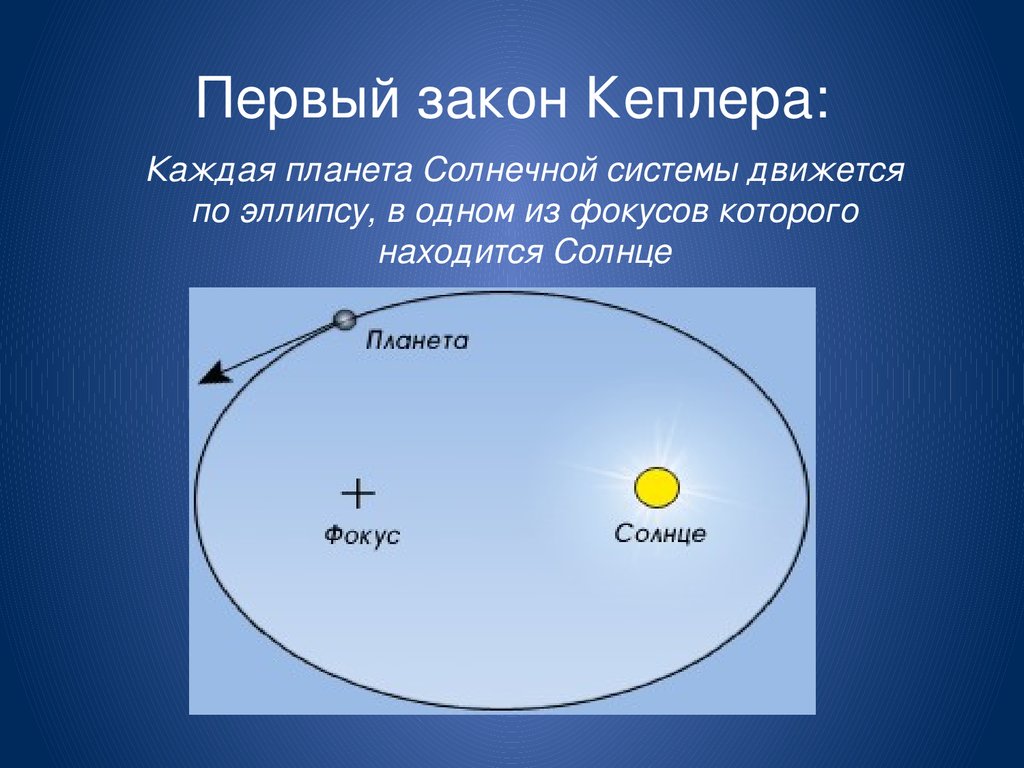
Первый закон Кеплера: каждая планета обращается вокруг Солнца по эллипсу, в одном аз фокусов которого находится Солнце.
Степень вытянутости эллипса характеризуется величиной его эксцентриситета. Эксцентриситет равен отношению расстояния фокуса от центра к длине большой полуоси. В пределе при совпадении фокусов и центра эксцентриситет равен нулю и эллипс превращается в окружность.
Ближайшая к Солнцу точка орбиты называется перигелием, а самая далекая от него точка называется афелием. Орбиты планет — эллипсы, мало отличающиеся от окружностей, их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е = 0,017.
Эксцентриситеты орбит у комет приближаются к единице. При е=1 второй фокус эллипса удаляется (в пределе) в бесконечность, так что эллипс становится разомкнутой кривой, называемой параболой. Ее ветви в бесконечности стремятся стать параллельными. При е>1 орбита является гиперболой. Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.
Кеплер открыл свои законы, изучая периодическое обращение планет вокруг Солнца. Ньютон, исходя из законов Кеплера, открыл закон всемирного тяготения. При этом он нашел, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу, в частности по кругу, по параболе и по гиперболе. Выяснилось, что некоторые кометы огибают Солнце, двигаясь по параболе или по гиперболе. В таком случае они уходят из солнечной системы и уже не являются ее членами.
Средняя скорость движения Земли по орбите 30 км/с. Орбита Земли близка к окружности, а скорость Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость для Земли будет равна √2*30 км/с = 42 км/с. При такой скорости относительно Солнца тело покинет солнечную систему.
Третий закон Кеплера: квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит.
Источник
Законы движения планет
В начале 17 века немецкий математик и астроном Иоганн Кеплер вывел три закона движения планет в Солнечной системе. Они были выведены на основании наблюдений за небесными телами, сделанных Браге и другими исследователями космического пространства того времени.
Первый закон Кеплера
Кеплер обратил внимание, что результаты наблюдений Браге расходятся с представлениями о круговой траектории обращения планет вокруг Солнца. Особенно это касалось Марса, чья траектория движения по наблюдения датчанина никак не могла описывать идеальный круг. Браге был очень точен в своих расчетах и сомнений в их правдивости у его последователя не возникло.
Тогда немецкий математик принял орбиты за эллипсы, у каждого из которых есть два фокуса. Это условные точки, выбранные таким образом, что сумма расстояний от них до любой точки эллипса – величина постоянная. При этом для эллиптической орбиты в одном из фокусов находится Солнце.
Форма эллипса вычисляется благодаря отношению фокального расстояния к большой полуоси орбиты. Полученное значение описывает эксцентриситет орбиты. Если он равен нулю – орбита представляет собой идеальную окружность, от нуля до единицы – эллипс различной вытянутости, больше единицы – параболу.
Второй закон Кеплера
Если орбита – это эллипс, то каким образом происходит движение небесного тела по ней? В каких отрезках орбитального пути оно ускоряется и замедляется?
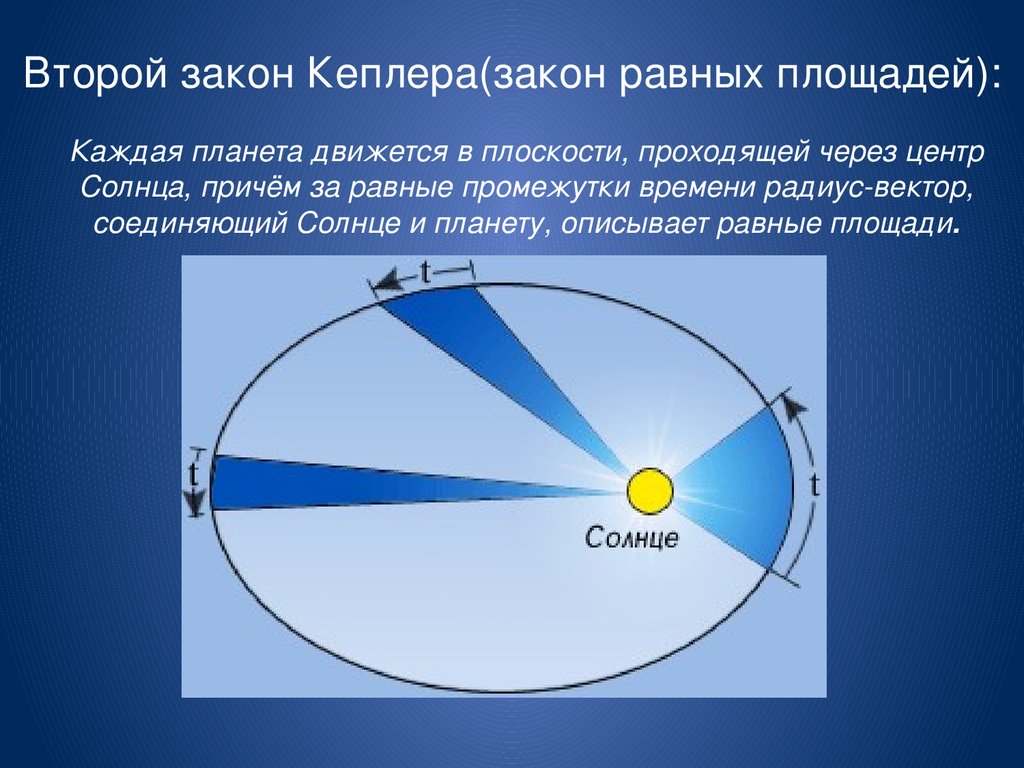
Немецкий ученый обнаружил, что есть взять два любых отрезка орбитального пути, которые планета Солнечной системы проходит за одинаковые промежутки времени, провести от их концов радиус-векторы к центральной звезде, то площади полученных образований будут одинаковы. Это упрощенная формулировка второго закона.
Для того, чтобы постоянство площадей сохранялось, тело должна двигаться в разных точках орбиты с разной скоростью. Так, например, Земля в наибольшем приближении к Солнцу движется быстрее, чем в максимальном удалении от него
Третий закон Кеплера
Третий постулат о движении небесных тел в Солнечной системе как раз касается понятий перигелия и афелия. Если провести между ними условную линию, получится большая ось траектории обращения планеты. Соответственно, половина этого отрезка – большая полуось.
Кеплер на основании наблюдений вывел, что отношение полных оборотов вокруг центральной звезды для двух любых планет системы, возведенных в квадрат, всегда равняется отношению больших полуосей орбитальных путей этих тел, возведенных в куб.
Трудность в доказательстве и принятии трех законов состояла в том, что он вывел их эмпирически. Но в конце 17 века Ньютоном был открыта классическая теория тяготения. Он и помог установить правильность суждений немецкого астронома и описал движение планет по эллипсу вокруг Солнца. Ньютон установил, что кроме массы объекта и его удаления от звезды никакие другие свойства не влияют на гравитационное притяжение.
Также Ньютон внес корректировки и в третий постулат Кеплера. Он открыл, что для соблюдения соотношения необходимо учитывать массу космического объекта. Данная трактовка третьего закона помогает установить массу планеты или спутника, зная величину его орбиты и период обращения.
Законы Иоганна Кеплера помогли установить форму планетарной траектории, вычислить период обращения планет, их скорость и ее изменения по мере приближения и удаления от Солнца. Ученый вывел Землю из ранга особенных астрономических объектов системы и установил, что она подчиняется всем трем законом, как и любая другая планета нашей звездной системы.
Источник
Законы движения Кеплера
Иоганн Кеплер и планеты Солнечной системы
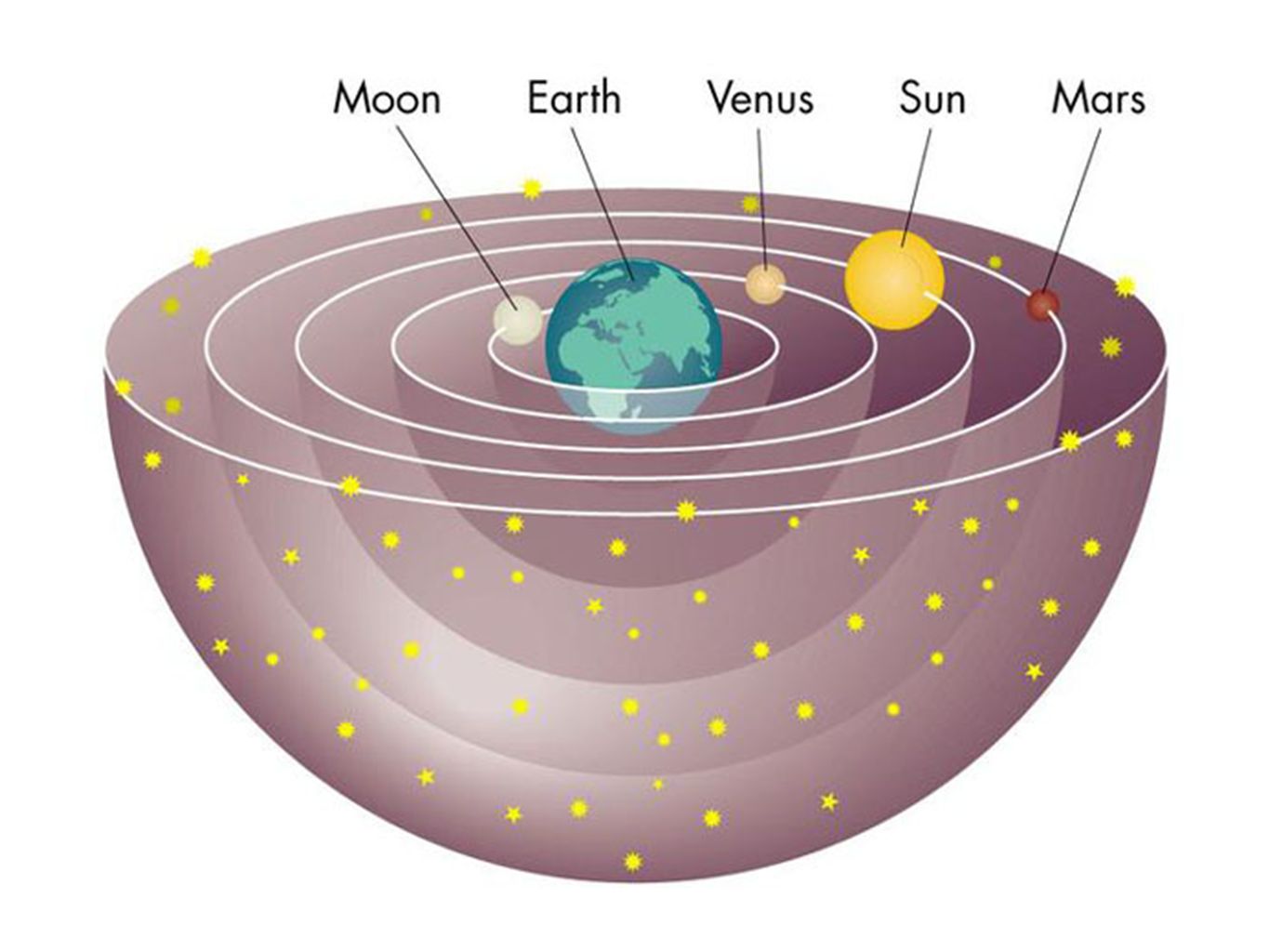
Астрономия конца XVI века отмечает столкновение двух моделей нашей Солнечной системы: геоцентрическая система Птолемея – где центром вращения всех объектов является Земля, и гелиоцентрическая система Коперника – где Солнце является центральным телом.
Модель Солнечной системы Клавдия Птолемея
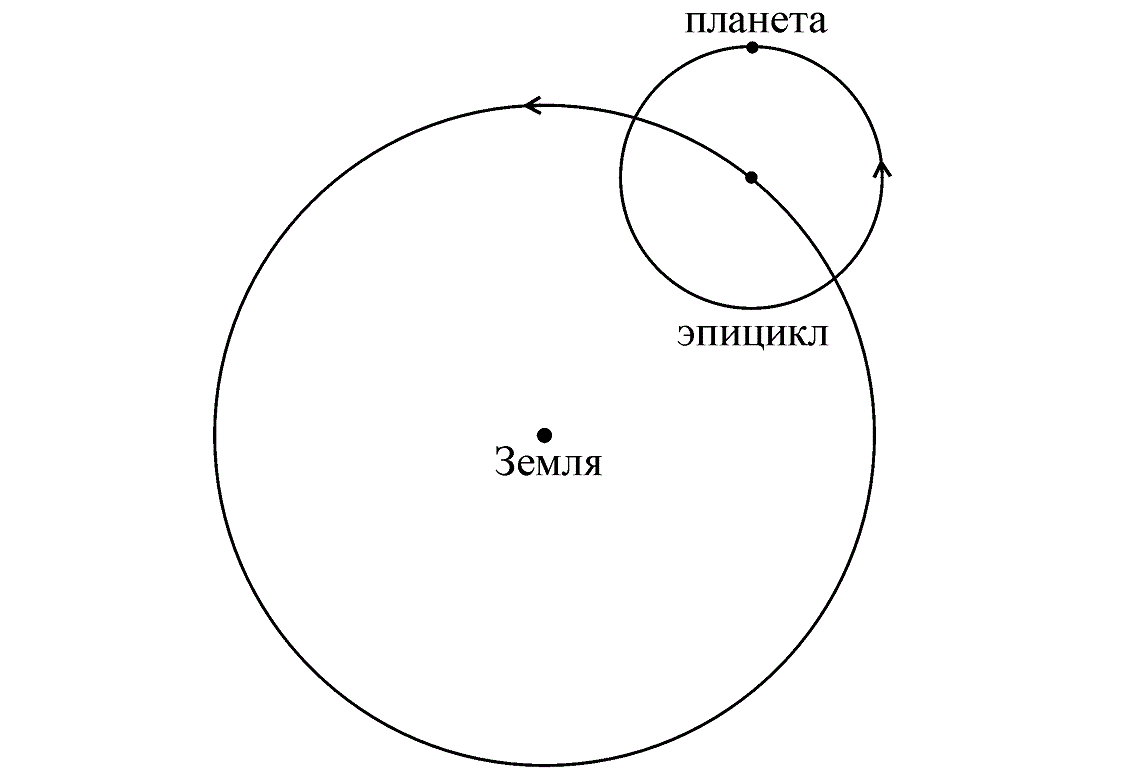
И хотя Коперник был ближе к истинной природе Солнечной системы, его работа имела недостатки. Основным из этих недостатков являлось утверждение, что планеты вращаются вокруг Солнца по круговым орбитам. С учетом этого, модель Коперника практически настолько же не согласовывалась с наблюдениями, как и система Птолемея. Польский астроном стремился исправить данное расхождение при помощи дополнительного движения планеты по кругу, центр которого уже двигался вокруг Солнца — эпицикл. Однако, расхождения в большей своей части не были устранены.
В начале XVII века немецкий астроном Иоганн Кеплер, изучая систему Николая Коперника, а также анализируя результаты астрономических наблюдений датчанина Тихо Браге, вывел основные законы относительно движения планет. Они были названы как Три закона Кеплера.
Первый закон Кеплера
Немецкий астроном пытался различными способами сохранить круговую орбиту движения планет, однако это не позволяло исправить расхождение с результатами наблюдений. Потому Кеплер прибегнул к эллиптическим орбитам. У каждой такой орбиты есть два так называемых фокуса. Фокусы – это две заданные точки, такие, что сумма расстояний от этих двух точек до любой точки эллипса является постоянной.
Иоганн Кеплер отметил, что планета движется по эллиптической орбите вокруг Солнца таким образом, что Солнце располагается в одном из двух фокусов эллипса, что и стало первым законом движения планет.
Первый закон Кеплера
Второй закон Кеплера
Проведем радиус-вектор от Солнца, которое располагается в одном из фокусов эллипсоидной орбиты планеты, к самой планете. Тогда за равные промежутки времени данный радиус-вектор описывает равные площади на плоскости, в которой движется планета вокруг Солнца. Данное утверждение является вторым законом.
Второй закон Кеплера
Третий закон Кеплера
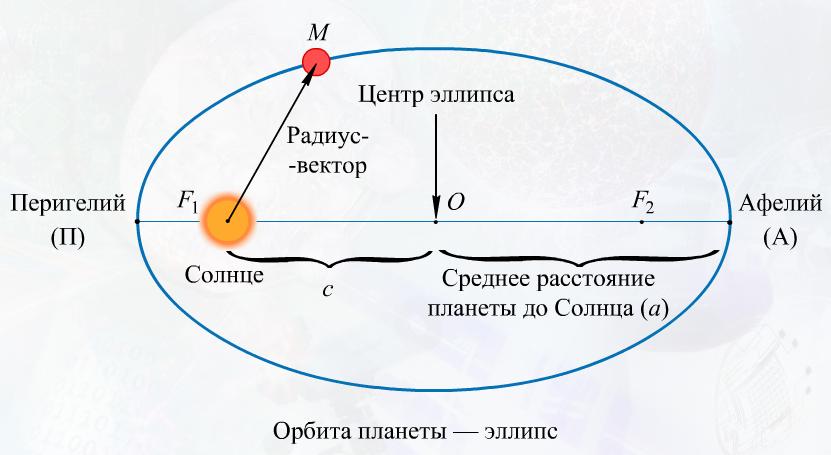
Каждая орбита планеты имеет точку, ближайшую к Солнцу, которое называется перигелием. Точка орбиты, наиболее удаленная от Солнца, называется афелием. Отрезок, соединяющий эти две точки называется большой осью орбиты. Если разделить этот отрезок пополам, то получим большую полуось, которую чаще используют в астрономии.
Основные элементы эллипса
Третий закон движения планет Кеплера звучит следующим образом:
Отношение квадрата периода обращения планеты вокруг Солнца к большой полуоси орбиты этой планеты является постоянным, и также равняется отношению квадрата периода обращения другой планеты вокруг Солнца к большой полуоси этой планеты.
Также иногда записывают другое отношение:
Одна из записей третьего закона
Дальнейшее развитие
И хотя законы Кеплера имели относительно невысокую погрешность (не более 1%), все же они были получены эмпирическим способом. Теоретическое же обоснование отсутствовало. Данная проблема позже была решена Исааком Ньютоном, который в 1682-м году открыл закон всемирного тяготения. Благодаря этому закону удалось описать подобное поведение планет. Законы Кеплера стали важнейшим этапом в понимании и описании движения планет.
‘ alt=»yH5BAEAAAAALAAAAAABAAEAAAIBRAA7 — Законы движения Кеплера» title=»Законы движения Кеплера»>
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Источник
Законы Иоганна Кеплера — великого философа, астронома и математика
В своё время, Кеплер на основании анализа наблюдений других учёных, Тихо Браге и Коперника, вывел три закона. Которые дают описание гелиоцентрической орбиты планеты. Основу его соотношений составили опыт и эксперименты.
Считается, что погрешность кеплеровых законом максимум 1%. Между тем, Кеплер не смог сам научно обосновать свои выводы. Более того, можно сказать, что выдвинул он их интуитивно. Впоследствии данные предположения теоретически доказал Исаак Ньютон. Также в дальнейшем их применение было обоснованно классической механикой.
Бесспорно, работы ученого в значительной мере способствовали пониманию внутренней системы движения космических объектов.
Познавать означает сопоставлять воспринятое извне с внутренними идеями и выносить суждение о том, насколько то и другое совпадает.
Первый закон Кеплера
Это эллипсический закон.
В нашей системе планеты осуществляют оборот по эллипсу. К тому же, Солнце находится на одном из фокусов данной кривой.
Форму эллипса и его сходство с окружностью определяют эксцентриситетом. Это выражение сечения конуса в числовой мере. Более того, именно он указывает на степень отклонения от окружности.
Его вычисляют делением промежутка от центра до фокуса эллипса на большую полуось. Если расстояние равно нулю, соответственно эллипс будет являться окружностью.
Открытие и использование закона всемирного тяготения в астрономии является доказательством первого закона Кеплера. Закон всемирного тяготения установил то, что каждый объект во Вселенной притягивает другой объект по определённой линии. Которая, помимо всего прочего, соединяет центры их масс. Но в то же время является пропорциональной массе каждого объекта, и обратно пропорциональной квадрату расстояния между этими объектами. Разработал закон всемирного тяготения Ньютон.
Первый закон Кеплера взаимосвязан с ньютоновскими законами.
Во втором законе Ньютон утверждал и доказывал, что ускорение объекта является пропорциональной равнодействующей всех сил. Которые прилагаются к объекту. Кроме того, ускорение также является обратно пропорциональным массе объекта.
Второй кеплеровский закон
По другому, его называют законом площадей. Он сообщает, что каждая планета движется в определённой плоскости. Которая, к тому же, простирается через центр Солнца. Вдобавок радиус-вектор, объединяющий планету и Солнце, заметает собой равные площади за равные промежутки времени.
В Солнечной системе планеты движутся вокруг Солнца совсем непостоянно. Например, от самой ближней точки орбиты до главной звезды наблюдается большая скорость, чем от самой дальней точки.
Действительно, мы наблюдаем такое явление в начале года. Видимое движение Солнца проходит быстрее, нежели в другое время. Так как Земля в это время расположена на ближнем пункте орбиты. Кстати, её называют перигелий. А прямо противоположную точку, то есть самую отдаленную-афелий.
Третий закон Кеплера
Часто называют его название гармоничный закон. Он подразумевает, что период вращения планеты в квадрате вокруг Солнца относится, как куб большой полуоси орбиты планеты.
По правилам силы гравитации, закон Кеплера не совсем точен. Помимо всего прочего, в нём должна учитываться масса планеты.
Гармоничный закон с учётом закона тяготения актуально применять для измерения массы космического объекта. Но только, если установлены их орбиты.
Источник