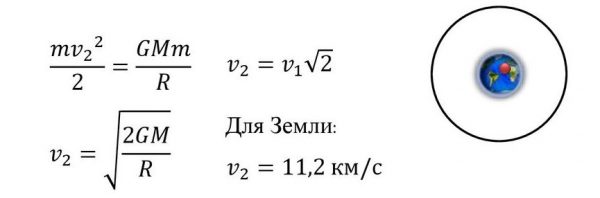Круговая скорость солнца равна
Брадлей в 1742 году обнаружил, что средние собственные движения звёзд почти по всему небу отличны от нуля и параллельны некоторому определенному направлению в пространстве. Естественно рассматривать это явление как результат движения Солнца относительно близких к нему звёзд. Изучение движения Солнца в пространстве явилось исторически первой задачей по исследованию звёздной кинематики.
Точка на небесной сфере, к которой направлено движение Солнца, называется апексом движения Солнца, или просто апексом, а диаметрально противоположная ей точка на небесной сфере — антиапексом. Само движение Солнца относительно окружающих его звёзд носит название движения к апексу. Составляющую собственного движения звёзд, вызванную движением Солнца к апексу, иногда называют, как уже говорилось в одной из предыдущих лекций, вековым параллаксом.
Можно рассматривать движение Солнца к апексу относительно всех наблюдаемых звёзд, или же относительно звёзд, отобранных по какому-либо признаку. В пространстве нет выделенной системы отсчёта, относительно которой можно было бы определить движение Солнца. Чтобы определить систему отсчёта, вводят понятие центроида группы объектов. Центроид задается всеми объектами рассматриваемой группы, а скоростью центроида считается средняя скорость движения этих объектов. Каждый из объектов, входящий в рассматриваемую группу (в том числе Солнце), имеет свою, так называемую пекулярную или остаточную скорость относительно центроида этих объектов. Очевидно, что сумма скоростей всех объектов относительно их центроида равна нулю. Центроид можно определить как точку, занимаемую Солнцем, движущуюся относительно его же со скоростью, равной средней скорости объектов в данном элементарном макроскопическом объеме пространства. Этот объем должен быть достаточно велик, чтобы в него попадало много объектов, но при этом составлять малую долю объема всей звёздной системы. Понятие центроида применимо к любой точке объема Галактики. При таком определении понятия центроида звёздная система приобретает свойство непрерывности , а скорости центроидов определяют ее поле скоростей .
Движение Солнца относительно центроида визуально ярких звёзд до 5 m — 6 m , среди которых встречаются как близкие звёзды, так и далекие гиганты и сверхгиганты, получило название стандартного движения Солнца . Округленные значения сферических экваториальных координат точки неба, в которую направлен вектор остаточной скорости Солнца (координаты стандартного апекса) приняты равными A=18 h , D=+30°, а величина скорости движения к апексу равна V0 = 19.5 км/с. Соответствующие координаты стандартного апекса в галактической системе координат есть L = 56°, B = +23°. Компоненты скорости Солнца в галактической системе координат получим по формулам:
 |
Отсюда возможно и обратное преобразование:
 |
Для стандартного апекса в галактической системе координат имеем: u0 = -10.2км/с, v0 = +15.1 км/с, w0 = +7.4 км/с.
Кроме выделяют так называемое основное движение Солнца , относя его к центроиду близких (в пределах, например, 25 пк от Солнца) звёзд главной последовательности. Оно определяется следующими величинами: V0 = 15.5 км/с, L = 45°, B = +24°. Определение движения Солнца относительно этой группы звёзд более обосновано, чем определение движения относительно разнородной совокупности ярких звёзд.
Наконец, движение Солнца относительно центра инерции Галактики получится прибавлением к основному движению Солнца линейной скорости вращения Галактики на солнечном галактоцентрическом расстоянии, с которой, по предположению, движется центроид окружающих Солнце близких звёзд.
Определить движение Солнца относительно избранного центроида нетрудно по лучевым скоростям объектов, определяющих центроид. Если известны расстояния до объектов, компоненты движения Солнца можно определить и по собственным движениям. Для определенности возьмем объектами нашей выборки звёзды, хотя скорость Солнца можно определять и относительно звёздных скоплений, отдельных газовых облаков, планетарных туманностей и других объектов.
Пусть единственной, кроме остаточной скорости звезды, составляющей движения является отражение движения Солнца в пространстве. Тогда для лучевых скоростей и собственных движений можно записать:
В выражениях (9-3) в правых частях штрихами обозначены остаточные компоненты скорости звезды, которые для больших объемов выборок должны согласно определению центроида в среднем компенсироваться. Поэтому можно принять их равными нулю и использовать выражения (9-3) для получения оценок величин компонентов движения Солнца в пространстве методом наименьших квадратов.
Движение Солнца в пространстве, как величина, определяющая систему отсчёта скоростей в Галактике, неоднократно определялось разными авторами относительно различных центроидов. В таблице 9-1 приведены некоторые из этих определений, взятые из работ различных исследователей. В первом столбце таблицы указаны объекты, относительно которых определено пространственное движение Солнца, а в шести последующих — величина этого движения.
|
Для наименьших значений движения Солнца (первые шесть строк таблицы 9-1) ошибки каждого компонента составляют (1 — 2) км/c, для остальных — несколько больше. Хорошо видно, что движение Солнца в пространстве разделяет объекты Галактики по кинематическим признакам на две подсистемы. К первой подсистеме относится большинство звёзд окрестностей Солнца с умеренными скоростями, к этой же подсистеме относятся рассеянные звёздные скопления и зоны HII, при этом более старые объекты показывают несколько большее движение. Очень сильно от этих подсистем отличаются по кинематическим признакам шаровые звёздные скопления, звёзды типа RR Лиры и субкарлики. Отметим, что межзвёздная среда по кинематическим характеристикам не отличается от большинства звёзд окрестностей Солнца.
Отдельно рассмотрим определение скорости Солнца относительно звёзд с круговыми галактическими орбитами. Дело в том, что имеется способ однозначно, независимо от выборки объектов определить точку отсчёта скоростей в окрестности Солнца, связав ее с круговой скоростью движения в Галактике , определив ее как скорость движения по круговой орбите на расстоянии Солнца от центра Галактики. У звёзд, движущихся по орбитам близким к круговым, остаточные скорости должны быть близки к нулю. Для определения движения Солнца относительно центроида звёзд, движущихся по круговым орбитам, необходимо создать большую выборку звёзд и постепенно удалять из нее звёзды с большими остаточными скоростями. В первой строке таблицы 9-1 движение Солнца было определено по выборке ОВ-звёзд окрестностей Солнца (около 450 звёзд), половина из которых была удалена как имеющая наибольшие остаточные скорости относительно среднего значения. Такой выбор базового центроида фиксирует систему отсчёта к наиболее молодым близким звездам поля, которые, по предположению, должны двигаться по круговым орбитам, как и межзвёздная среда, из которой они образовались. (Последнее утверждение верно лишь приблизительно, поскольку, как будет отмечено ниже, основная масса близких ОВ-звёзд принадлежит движущемуся относительно круговой скорости на солнечном галактоцентрическом расстоянии Поясу Гулда.) Одновременно и остаточные скорости самых разных объектов можно изучать относительно одного центроида, связанного физически с Галактикой в целом.
Движение Солнца в пространстве определяет систему отсчёта скоростей в окрестностях Солнца, так называемую локальную систему покоя (английская аббревиатура — LSR).
Источник
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
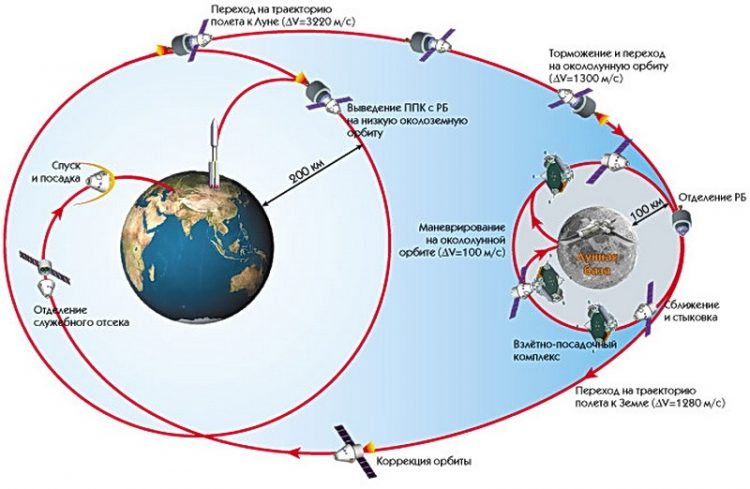
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
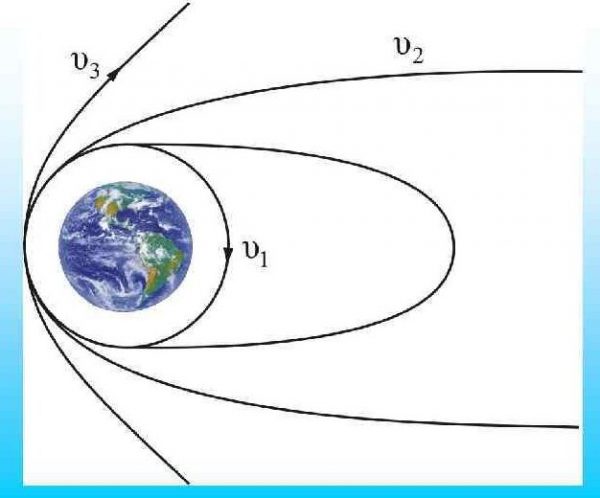
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
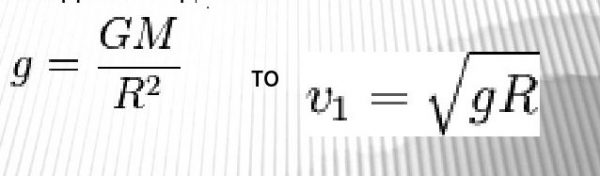
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
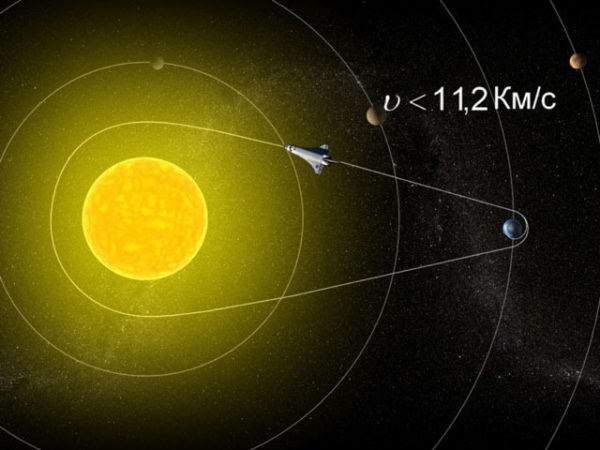
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник