Космос плоский или нет

Почему Вселенная плоская, а не сферическая?

Значение Большого взрыва очень часто неправильно понимают. Считается, что что-то взорвалось где-то, а затем взорванная часть расширилась до того места, где мы сейчас находимся. Это не правильно. До Большого взрыва не было ни пространства, ни времени. Таким образом, нет ничего «вне» Большого взрыва. Вселенная просто расширилась от очень маленького объема до огромного объема, и это расширение происходит даже сегодня. Итак, место, где мы сейчас находимся, соответствует некоторому месту в очень маленьком объеме в самой ранней Вселенной. Следовательно, Большой Взрыв произошел ВЕЗДЕ во Вселенной. Это происходило во всех местах, включая то место, где мы сейчас находимся.

Почему Вселенная выглядит плоской? Это был один из сложных вопросов в космологии долгое время. Сегодня большинство астрономов верят в теорию инфляции (и есть доказательства, подтверждающие это). Согласно этой теории, Вселенная подверглась экспоненциальному расширению примерно через 10-30 секунд после Большого взрыва. В результате к концу инфляционной эпохи что-то размером с атом расширилось до размеров Солнечной системы.

Если бы это было так, независимо от исходной геометрии Вселенной, это казалось бы нам плоским. Аналогия будет взять воздушный шар; мы можем легко увидеть его округленным; Теперь взорвите шарик до очень большого объема, а затем положите на его поверхность маленького муравья. Муравей будет думать, что это на листе; он не может обнаружить кривизну. Иными словами, расстояния, которые мы исследуем, слишком малы, чтобы обнаружить любую возможную кривизну во Вселенной.

Если, как вы говорите, «расстояния, которые мы исследуем, слишком малы, чтобы обнаружить любую возможную кривизну во Вселенной» . как мы можем принять недавние «доказательства» плоской вселенной? Все попытки доказать плоскостность или нет вселенной ограничены данными, собранными из наблюдаемой вселенной? Если это так, и мы предполагаем, что наш взгляд эквивалентен взгляду близорукого муравья на земле, то, безусловно, невозможно найти такое доказательство, если, конечно, информация не может распространяться быстрее света.

Во-первых, вы должны различать «вселенную» и «наблюдаемую вселенную». Технически, «вселенная» представляет собой все, что существует, в то время как «наблюдаемая вселенная» представляет собой все, что существует внутри нашего горизонта (то есть объем вселенной, в которой свет успел добраться до нас). Каждое наблюдение, которое мы можем когда-либо сделать, ограничено наблюдаемой вселенной, и у нас нет никакого способа точно знать, что происходит за горизонтом. Но многие люди используют «вселенную» как сокращение от «наблюдаемой вселенной», что может создать некоторую путаницу. Поэтому, когда мы говорим «WMAP предоставляет убедительные доказательства того, что Вселенная плоская», мы действительно имеем в виду «WMAP предоставляет убедительные доказательства того, что наблюдаемая Вселенная плоская».

WMAP (англ. Wilkinson Microwave Anisotropy Probe) — космический аппарат НАСА, предназначенный для изучения реликтового излучения, образовавшегося в результате Большого взрыва. Запущен 30 июня 2001 года.

Однако, согласно теории инфляции, даже если у вселенной есть некоторая кривизна, наблюдаемая вселенная должна быть плоской на уровне, на котором мы можем ее измерить. Но мы не * знаем *, что теория инфляции верна. Так что да, важно проводить эксперименты, подобные тем, которые проводятся WMAP. Если бы мы обнаружили отклонения от плоскостности в наблюдаемой вселенной, то это дало бы доказательства против инфляции.

Источник

Плоский космос

Подскажите фантастический роман, повесть (или фильм) в котором космические корабли приближаются к Земле не со стороны Плутона, Нептуна, Урана. А под заметным углом к эклиптике. А то что ни читаю – ракета, двигаясь к Земле из глубин космоса, обязательно пролетает мимо всех планет Солнечной системы, будто они специально выстраиваются вдоль траектории космического корабля.

Распространённый способ упростить управление в битвах в играх жанра стратегии — это сделать плоский космос. Плоский космос также популярен и в аркадах, вроде «Космических рейнджеров». Педаль в пол — если космос изображается вообще линейным. Это когда попасть с Нептуна, например, на Землю можно только минуя последовательно Уран, Сатурн, Юпитер, Марс и Луну, хотя в реальности эти небесные тела вовсе не обязаны вас поджидать в том самом месте, где вы будете пересекать их орбиты, и вполне могут находиться на противоположной от вас стороне.

Часто звёздные скопления в плоском космосе называют созвездиями. Не совсем верно (созвездие — это область звёздного неба), но так проще.

Содержание

Где встречается (не в играх) [ править ]

Seikai no Saga — гиперпространство дословно называется, «плоский космос», планар. Оно не просто плоское, оно истинно двухмерное. Корабли в нём летают в собственных пузырях обычного пространства, в планаре выглядящих массивными точками. Для сражений пузыри соединяют, потому перестрелки проходят почти всегда прямо в упор.
Роман Злотников, «И пришёл многоликий…» — в тексте прямым текстом сказано, что защитные сооружения в космосе образуют оборонительные кольца.
Реальная жизнь — большинство «обычных» галактик (и, скорее всего, планетных систем) вытянуты в плоскости вращения. Летать «поперёк» никто не запрещает, но смысл?
- Смысл в том, что эти «плоскости» не такие уж плоские. Даже в масштабах планетной системы существуют объекты, отстоящие от «общей» плоскости эклиптики на многие миллионы километров. О галактиках и говорить нечего. Наглядный пример: не считая очень далёкий Млечный Путь, звёзд на небе видно не одинаково много в любом направлении, в некоторых направлениях звёзд настолько много, что они сливаются во Млечный Путь в котором отдельные звёзды (кроме самых ярких сверх-гигантов) невооружённым взглядом не различить [1] .
Обстёбано в интернет-комиксе «Глубина заблуждения». Главные герои игнорируют блокаду планеты Нибиру именно потому, что планету «взяли в кольцо».

Где НЕ встречается (в играх) [ править ]

В случае игр проще назвать, где не встречается, чем перечислить все игры, где встречается.

Star Control (самый первый). Чтобы понятно было, что космос трёхмерный, он постоянно крутится вокруг оси.
Homeworld. Хотя за редкими (эпичными) исключениями всё интересное находится и происходит недалеко от базовой плоскости карты.
Nexus: the Jupiter incident
Star Wars: Rebellion
Старые DOSовские Star Wars: X-Wing, Star Wars: TIE Fighter, как и их потомки. Хотя сражения происходят, большей частью, в одной плоскости, сам движок вполне трёхмерен, что иногда позволяет любопытные финты. Так, в одной из миссий нужно пролететь на истребителе через зону массового боя, чтобы подойти на нужное расстояние к цели и сбросить торпеды. Так вот, можно просто отключить в самом начале оружие и защиту, дать всю мощность на движки и облететь зону боя сверху/снизу по дуге. Противники гонятся (то есть ИИ вполне себе понимает третье измерение), но тупо не успевают.
В Elite: Frontier космос условно не плоский: у каждой звезды присутствует z-координата, что приходится учитывать при прокладке гиперпрыжков, особенно если гипердвигатель слабый. Однако разброс по этой z-координате ничтожен (плюс-минус 10 световых лет, помню плохо и с цифрой могу ошибиться, поправьте, если не права) по сравнению с бескрайней шириной галактики по x и y.
А вот в Elite: Dangerous космос уже не плоский совсем. То есть да, галактика спиральная и в межгалактических масштабах плоская, но игроку от этого не легче, 1000 световых лет (при среднем расстоянии между системами в 10-15) по оси z найти довольно легко.
Stellaris — звёзды и корабли тут лежат не на плоскости, хоть и на геймплей это никак не влияет из-за особенностей сверхсветового перемещения и автоматизированных сражений.
Spore — почти то же самое. Внезапно большая z-координата может неприятно удивить, не дав переместиться в желаемую систему, но не более.
Star Citizen — никакой гравитации, никаких мух в меду… короче, взлёт-посадка без автопилота — уже задача не самая тривиальная.
«Звёздные волки» со всеми продолжениями — игровые локации имеют имеют 3 оси координат.
Ascendancy — муха в меду, но хотя бы в трёхмерном. Минус — все планетные системы соосны. Обоснуй — весь кластер зародился в одном космогоническом процессе.
Haegemonia: Legions of Iron — все небесные тела лежат в плоскости эклиптики, однако корабли могут летать куда хотят, вот только зачем?
- Периодически используется ИИ. При обнаружении корабля-шпиона близ планеты компьютер постоянно норовит увести его вниз от планеты. Забавно, что в какой-то момент он утыкается в невидимую стену уровня и прекращает движения, покорно отдаваясь на растерзание преследующим его истребителям. Кроме того, компьютер иногда отправляет путешествовать парочку боевых звеньев сильно выше орбитальной плоскости, дабы позже «неожиданно» атаковать планеты игрока сверху. Можно использовать и самому для обхода групп кораблей противника и/или военных баз. Впрочем, переоценивать данные маневры всё же не стоит: в кампании в подавляющем большинстве случаев лобовая атака группой прокачанных кораблей и с героями на борту проще и эффективней, благо низкая скорость и огневая мощь тяжелых кораблей способствуют именно этому варианту.
Sword of the Stars. Если специально не делать плоскую карту, то ближе к концу игры вполне можно заработать вывих мозга, пытаясь определить свои границы, так как экспансия идет по всем трем измерениям.
Starmade — полноценный объёмный космос.

С особо популярным фитильком [ править ]

Типичный результат того, что автор тупо перенёс реальные морские тактики и сражения в космос, а то, что космос отнюдь не плоский, «компенсировал» тем, что просто напрямую заменил линии на стенки. Результат плоским не выглядит, однако в сколь-либо длительной битве бросается в глаза, что стенки привязаны к определённой плоскости.

Legend of Galactic Heroes — большинство космических битв срисованы с реальных морских сражений, соответственно, о существовании третьего измерения почти никогда не вспоминают. То есть тактически битвы получаются плоские, но визуально битвы в аниме отнюдь не выглядят плоскими, так как корабли строятся не в линии, как в морских сражениях и компьютерных играх с плоским космосом, а в строго вертикальные стенки. Ключевой момент — «строго вертикальные», то есть всё было бы хорошо, если бы эти стенки отклонялись бы от строгой вертикали.
- Справедливости ради, иногда герои отходят от двухмерной тактики. Обоснуем может послужить трудность реализации и возможная её опасность. Корабли в ЛОГГ — это курсовые пушки с основным двигателем позади. При таком строении в корабль можно зарядить куда более мощное орудие (собственно, треть корабля — это большая лазерная пушка с огромной дальностью), в него труднее попасть, если корабли стоят лоб в лоб, и легче защитить силовым полем. С боков же корабли особо уязвимы и большинство битв выигрывается именно за счёт грамотного окружения, а «окружая» врага с трёх измерений собственный флот тоже подставляется под удар, ведь корабль врага может взять немного выше и расстрелять незадачливого тактика в корпус.
Да и в цикле книг о Хонор Харрингтон примерно то же самое наблюдается. Там даже линейные корабли называют кораблями стены. Фитилёк отгорел к переходу сражений на перестрелки тысячами ракет с астрономических расстояний.
Полностью отсутствует в цикле «Потерянный флот», где адмиралу приходится думать не только в трёх измерениях, а в четырёх (т. е. время)! Ведь без сверхсветовых локаторов и средств связи, можно только гадать что сейчас делает вражеский флот в двух световых часах от тебя (всё, что ты видишь сейчас — устарело на два часа). Автор старался сделать помесь современных морских сражений и воздушного боя. Хотя сражения описаны подробно, читатель должен сам быть чуть ли не тактическим гением сражений в космосе, чтобы разобраться.

Источник

Спросите Итана: почему Вселенная плоская?

Двигаясь по прямой линии в гиперторовой модели Вселенной, вы вернётесь в исходную точку, даже если пространство-время не будет искривлённым. Также Вселенная может быть замкнутой, имея положительную кривизну – как гиперсфера.

Какой формы Вселенная? Если бы вы жили до XIX века, вам бы, наверное, не пришло в голову, что у Вселенной вообще может быть какая-то форма. Вы, как и все остальные, начали бы изучать геометрию с правил Евклида, для которого пространство было всего лишь трёхмерной решёткой. Затем вы применяли бы физические законы Ньютона, и предполагали, что взаимодействия двух любых объектов направлены вдоль одной прямой линии, их соединяющей. Но с тех пор мы очень многое поняли. Пространство не просто искривляется в присутствии материи и энергии – мы можем это наблюдать. И всё же, если речь заходит о Вселенной в целом, пространство ничем не отличается от идеально плоского. Почему? На эту тему задаёт вопрос и наш читатель:

Почему вселенная относительно плоская, а не имеет форму сферы? Разве вселенная не будет расширяться перпендикулярно к плоской поверхности?

Давайте начнём со старого определения пространства, которое большинство из нас и представляет: в виде некоей трёхмерной решётки.

Мы часто представляем себе пространство в виде трёхмерной решётки, несмотря на то, что с точки зрения концепции пространства-времени это чрезмерное упрощение картины, зависящее от системы отсчёта. На самом деле пространство-время искривляется в присутствии материи и энергии, а расстояния не остаются неизменными, меняясь с расширением или сжатием Вселенной.

В Евклидовой геометрии, которую учило большинство из нас, есть пять постулатов, из которых можно вывести всё остальное.

Две любых точки можно соединить отрезком прямой.
Любой отрезок прямой можно продлить до бесконечности.
Любой отрезок можно использовать для создания круга, где один его конец будет в центре, а другой опишет окружность.
Все прямые углы одинаковы, и равняются 90° (или π/2 в радианах).
Параллельные прямые нигде не пересекаются.

Прим. пер.: пятый постулат Евклид формулировал так: «если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов». То есть, если одна прямая пересекает две других под прямыми углами, то те две прямые параллельны.

Всё, что вы рисовали на бумаге, подчиняется этим правилам, и всем нам известно представление о том, что Вселенная просто подчиняется трёхмерной версии правил Евклида.

Но это не обязательно так, и всё дело в пятом постулате. Чтобы понять это, посмотрим на линии долготы на глобусе.

Диаграмма Земного шара, отцентрированная на линии перемены дат, где также видно линии широты и долготы. На экваторе все линии долготы параллельны, но они всё равно пересекаются в двух местах: на Северном и Южном полюсах.

Любая линия долготы совершает полный круг, обходя Землю, пересекая экватор под углом в 90°. Поскольку экватор прямой, и все линии долготы – прямые, получается, что по определению на экваторе линии долготы параллельны. И если бы пятый постулат Евклида был истинным, то две линии долготы не могли бы пересекаться.

Но линии долготы пересекаются. Все они пересекаются в двух точках: на Северном и Южном полюсах.

По этой же причине нельзя развернуть сферу и разложить её на плоскости в квадрат: поверхность сферы фундаментально искривлённая и не плоская. Вообще существует три типа фундаментально отличных поверхностей в пространстве. Есть поверхности положительной кривизны, как сфера; поверхности отрицательной кривизны, как седло; и поверхности нулевой кривизны, как плоский лист бумаги. Если вам нужно узнать кривизну поверхности, вам нужно всего лишь нарисовать на ней треугольник. При этом кривизну будет измерить тем легче, чем он будет больше. Затем нужно просто измерить величину трёх его углов и сложить.

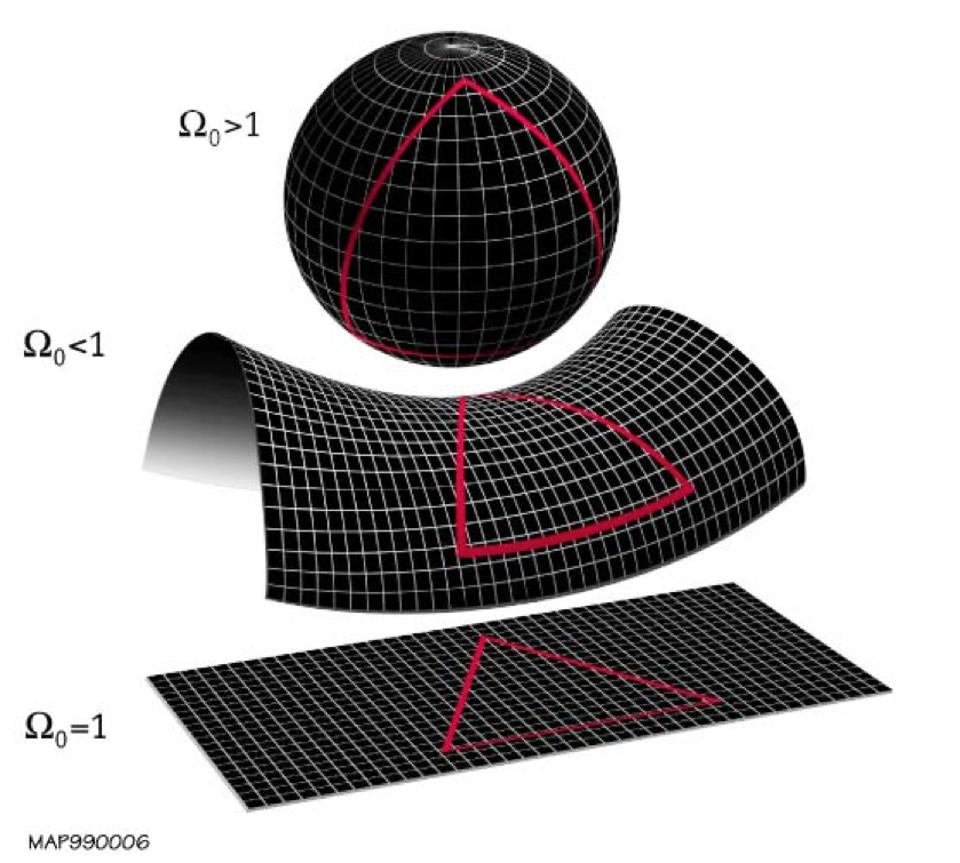
В зависимости от пространственной кривизны сумма получится разной. У Вселенной с положительной кривизной (вверху), отрицательной (в середине) или с нулевой (внизу) сумма углов треугольника окажется больше, меньше или равной 180° соответственно.

Большинство из нас знает, что будет, если нарисовать треугольник на плоском, не искривлённом листе бумаги. Три его внутренних угла дадут в сумме 180°. Но если вы возьмёте поверхность положительной кривизны, например, сферу, ваша сумма будет больше 180°, и чем больше треугольник относительно радиуса сферы, тем больше будет сумма. Если же вы возьмёте поверхность отрицательной кривизны, типа седла или гиперболоида, сумма внутренних углов всегда будет меньше 180°, и чем больше будет треугольник, тем больше сумма будет отличаться от 180°.

Идея о существовании фундаментально искривлённых поверхностей, не подчиняющихся пятому постулату Евклида, на которых параллельные прямые могут пересекаться или расходиться, почти 200 лет назад привело к появлению новой области, неевклидовой геометрии. Работали над ней и опубликовали свои работы в 1820-1830-х годах независимо российский математик Николай Иванович Лобачевский и венгерский математик Янош Бойяи. Эту идею далее развил Бернхард Риман, расширив её на произвольное количество измерении, и первым записал то, что сегодня известно нам, как метрический тензор, различные параметры которого описывают кривизну конкретной геометрии.

В начале XX века Альберт Эйнштейн использовал метрический тензор Римана для разработки Общей теории относительности: четырёхмерной теории пространства-времени и гравитации.

Иллюстрация гравитационного линзирования показывает, как изображение фоновых галактик, или любой луч света, искажается в присутствии массы. Но ещё это показывает, как само пространство изгибается и искажается в присутствии на переднем фоне массы. Если несколько фоновых объектов выстраиваются в линию с одной гравитационной линзой, находящейся на переднем плане, правильно расположенный наблюдатель увидит несколько наборов из нескольких изображений.

Проще говоря, Эйнштейн понял, что нет смысла рассуждать об абсолютных пространстве и времени. В ОТО при путешествии со скоростью, близкой к световой, пространство будет сжиматься вдоль направления вашего движения, а время – замедляться. У разных наблюдателей, движущихся с разными скоростями, часы будут идти по-разному. Есть правила, по которым пространство и время преобразуются для каждого из наблюдателей, они были описаны в СТО для вселенной без гравитации.

Но в нашей Вселенной гравитация есть. В частности, наличие не только массы, но вообще любой формы энергии, заставляет ткань пространства-времени искривляться определённым образом. У Эйнштейна ушло полных десять лет (с публикации СТО в 1905 году до приведения ОТО с гравитацией в окончательный, правильный вид) на то, чтобы понять, как включить гравитацию в теорию относительности, основываясь на ранней работе Римана. И результат его работы, ОТО, до сих пор успешно проходил все экспериментальные испытания.

Что тут примечательно: применяя уравнения поля из ОТО к нашей Вселенной, заполненной энергией и материей, расширяющейся, изотропной (имеющей одинаковую среднюю плотность по всем направлениям) и гомогенной (имеющей одинаковую среднюю плотность во всех местах), мы обнаруживаем тесную взаимосвязь между тремя следующими величинами:

количеством материи и энергии всех видов во Вселенной,
скоростью расширения Вселенной на крупнейших масштабах,
кривизной наблюдаемой части Вселенной.

Автор этих строк на фоне видеостены в Американском астрономическом сообществе, рядом с первым уравнением Фридмана. Самый левый член уравнения — это хаббловская скорость расширения в квадрате, определяющая развитие пространства-времени. Правее идут члены, относящиеся ко всем различным формам материи и энергии, а справа описывается кривизна пространства, определяющая будущее развитие Вселенной. Это уравнение называют важнейшим для всей космологии. Его в 1922 году вывел Фридман, практически в современном виде.

В самые первые моменты горячего Большого взрыва Вселенная была чрезвычайно горячей, плотной и крайне быстро расширялась. Поскольку в ОТО эволюция ткани пространства-времени так сильно зависит от содержащейся в ней материи и энергии, то такая Вселенная могла развиваться только тремя путями:

Если скорость расширения будет слишком малой для того количества материи и энергии, что есть во Вселенной, их общий гравитационный эффект замедлит скорость расширения, потом сведёт её к нулю, а потом заставит изменить знак на противоположный, что приведёт к сжатию. Вскоре Вселенная вновь схлопнется, придя к Большому сжатию.
Если скорость расширения будет слишком большой для того количества материи и энергии, что есть во Вселенной, их общий гравитационный эффект не только не сможет замедлить и обратить вспять расширение, он, возможно, даже не сильно его и замедлит. Опасность ускоренного расширения заключается в том, что довольно скоро во Вселенной исчезнет возможность формирования галактик, звёзд и даже атомов.
Если баланс двух этих величин будет как раз подходящим, получится Вселенная, вечно расширяющаяся и в изобилии формирующая в процессе богатые сложные структуры.

Последний вариант описывает нашу Вселенную, в которой всё хорошо сбалансировано. Но для этого нужна такая плотность материи и энергии, которая очень чётко соответствует скорости расширения с самых ранних времён.

Деликатный баланс между скоростью расширения и общей плотностью Вселенной настолько шаткий, что отклонение в любую сторону даже на 0,00000000001% приведёт к невозможности возникновения во Вселенной какой бы то ни было жизни, звёзд и даже, вероятно, молекул.

И то, что наша Вселенная существует, обладая наблюдаемыми нами свойствами, говорит о том, что на самом раннем этапе своей жизни она должна была быть очень приближена к плоской. У Вселенной со слишком большим количеством материи и энергии на данную скорость расширения была бы положительная кривизна, а со слишком малым – отрицательная. И только идеально сбалансированный случай даёт плоскую Вселенную.

Однако возможно, что Вселенная искривлена на чрезвычайно больших масштабах – возможно, больших, чем наблюдаемая нами часть Вселенной. Вы, наверное, представляете себе эксперимент по рисованию треугольника между нашим местоположением и двумя удалёнными галактиками и подсчёт суммы его углов. Но это можно будет сделать, только добравшись до этих галактик, чего мы пока не можем. В настоящее время технология не позволяет нам выбраться из нашего уголка Вселенной. Так же, как вы не можете точно измерить кривизну земной поверхности, не выходя со двора, мы не можем построить достаточно большой треугольник, будучи ограниченными пределами нашей Солнечной системы.

К счастью, мы можем провести два основных наблюдения, раскрывающих кривизну Вселенной. И оба они приводят нас к одинаковым выводам.

Различные угловые размеры флуктуаций реликтового излучения присущи разным вариантам пространственной кривизны. На сегодня Вселенная выглядит плоской, однако мы провели измерения с погрешностью в 0,4%. Если измерить точнее, возможно, проявится какая-либо кривизна – однако из имеющихся наблюдений следует, что даже если Вселенная имеет кривизну, её масштабы в 250 3 раз (более, чем в 15 млн раз) больше размера обозримой Вселенной.

1. Угловой размер флуктуаций температуры, наблюдаемых в реликтовом излучении

На ранних стадиях горячего Большого взрыва наша Вселенная была очень однородной – очень, но не идеально. В ней были крохотные несовершенства – участки, в которых плотность была чуть меньше или чуть больше средней. Наложились воздействия гравитации, притягивающей материю и энергию к более плотным участкам, и излучения, расталкивающего материю. В итоге получилось распределение флуктуаций температур, наложившее свой отпечаток на излучение, оставшееся от Большого взрыва, которое мы можем наблюдать: реликтовое излучение [или, как его называют в англоязычных источниках, космический микроволновой фон / прим. пер.].

У этих флуктуаций есть определённый спектр: они бывают теплее или холоднее на определённую величину на определённых масштабах расстояний. В плоской Вселенной эти масштабы выглядят такими, какие они есть. В искривлённой Вселенной они казались бы больше (при положительной кривизне) или меньше (при отрицательной). Судя по видимому размеру флуктуаций, которые мы наблюдаем при помощи космического телескопа «Планк» и других приборов, мы можем сказать, что Вселенная плоская с точностью до 99,6%.

Это говорит нам о том, что если Вселенная искривлена, масштаб этих искривлений в 250 раз больше наблюдаемой нами части Вселенной, диаметр которой составляет уже 92 млрд световых лет.

Можно заглянуть сколь угодно далеко в прошлое Вселенной, так далеко, как нам позволят наши телескопы, и скопления галактик дадут определённую шкалу расстояний – т.н. акустическую шкалу – развивающуюся во времени определённым образом. Подобный детальный анализ позволит понять, искривлена ли Вселенная, или же плоская.

2. Видимые угловые различия галактик, скапливавшихся в различные эпохи существования Вселенной

Существует определённая шкала расстояний, на которой вероятность скопления галактик увеличивается. Если выбрать сегодня любую галактику во Вселенной, и отойти от неё на определённое расстояние, можно задать вопрос: «какова вероятность найти другую галактику на таком расстоянии от первой?». Оказывается, что вероятность найти другую галактику велика на небольших расстояниях, и что эта вероятность при удалении будет падать определённым образом, с одной интересной характерной особенностью: вероятность найти другую галактику на расстоянии порядка 500 млн световых лет от первой будет чуть выше, чем на расстояниях в 400 или 600 млн световых лет.

Эта шкала расстояний расширялась вместе со всей Вселенной, поэтому в ранней вселенной «характерное расстояние» было меньше. Если бы Вселенная имела положительную или отрицательную кривизну, на эту особенность наложился бы дополнительный эффект. Это бы изменило видимые масштабы кластеризации галактик. То, что ничего подобного мы не наблюдаем, вкупе с результатами изучения реликтового излучения, даёт нам ещё более строгое ограничение: Вселенная плоская с точностью до 99,75%.

Иначе говоря, если Вселенная искривлена – к примеру, если это гиперсфера (четырёхмерный аналог трёхмерной сферы) – то её радиус должен быть по меньшей мере в 400 раз больше размера наблюдаемой Вселенной.

Квантовые флуктуации, появившиеся во время инфляции, растягиваются на всю Вселенную, а также вызывают флуктуации общей плотности энергии. Те, в свою очередь, вызывают появление несовершенств в ранней Вселенной, из-за которых и появляются температурные флуктуации, наблюдаемые нами в реликтовом излучении. По теории инфляции эти флуктуации должны быть адиабатическими.

Всё это говорит нам о том, откуда нам известно, что Вселенная плоская. Но чтобы понять, почему она плоская, нам нужно обратиться к теории нашего космического происхождения, приведшего к Большому взрыву: космической инфляции. Инфляция взяла Вселенную в том виде, в каком она была ранее, и растянула до огромных масштабов. К окончанию инфляции Вселенная оказалась гораздо больше: настолько огромной, что наблюдаемая нами часть неотличима от плоской.

Единственным отклонением от этой плоской картины будет сумма всех квантовых флуктуаций, растянувшихся по космосу во время самой инфляции. Насколько мы понимаем природу этих флуктуаций, их особенности дают новое предсказание, которое ещё только предстоит проверить с достаточной точностью: наблюдаемая нами Вселенная должна отличаться от идеально плоской картины на величину в диапазоне от 1/10 000 до 1/1 000 000.

Квантовые флуктуации, происходившие во время инфляции, растянулись на всю Вселенную, и по её окончанию превратились в флуктуации плотности. Со временем это породило крупномасштабные структуры сегодняшней Вселенной, а также температурные флуктуации, наблюдаемые нами в реликтовом излучении. Подобные новые предсказания необходимы для подтверждения предлагаемого механизма тонкой подстройки.

Пока что мы измерили кривизну с точностью до 1/400, и обнаружили, что от плоской она неотличима. Но если бы мы смогли добраться до сверхточных измерений, у нас была бы возможность подтвердить или опровергнуть предсказания ведущей теории космической эволюции на новом уровне. Мы не можем знать истинной формы Вселенной, но мы можем измерять и предсказывать её кривизну.

И хотя сегодня она кажется нам неотличимой от плоской, вполне может оказаться, что у неё есть небольшое, но реальное отклонение от нулевой кривизны. Через одно-два поколения, в зависимости от скорости технического прогресса, мы, возможно, узнаем, насколько наша Вселенная отличается от идеально плоской.

Источник