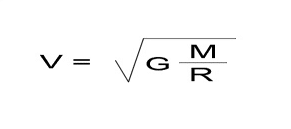Чему равна первая космическая скорость марса?
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
Первую космическую скорость можно определить через ускорение свободного падения —
Вычисление
Для того, чтобы покинуть пределы Солнечной системы с орбиты Земли, ракета массой m <\displaystyle m>должна обладать скоростью относительно Солнца vC<\displaystyle v_
где MC<\displaystyle M_
Ракета вследствие движения вместе с Землей по орбите вокруг Солнца уже обладает скоростью вращения Земли вокруг Солнца, которую можно найти, применив второй закон Ньютона:
Следовательно, при разгоне ракеты в направлении вектора скорости движения Земли по её орбите вокруг Солнца скорость космической ракеты vRZ<\displaystyle v_
Для того, чтобы удалить корабль из поля тяготения Земли, ему надо сообщить вторую космическую скорость
Следовательно, кинетическая энергия Ek<\displaystyle E_
Отсюда приходим к формуле:
где vZ<\displaystyle v_
Подставляя численные значения (для Земли vZ<\displaystyle v_
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Вторая космическая скорость
Основная статья: Вторая космическая скорость
Между первой и второй космическими скоростями в нерелятивистском случае существует простое соотношение:
Квадрат скорости убегания (второй космической скорости) равен удвоенному ньютоновскому потенциалу на поверхности тела, взятому с обратным знаком:
Вторая космическая скорость (параболическая скорость, скорость убегания) обычно определяется в предположении отсутствия каких-либо других небесных тел. Например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Источник
Первая космическая скорость Марса
Первая космическая скорость Марса — это не измерение темпов движения красной планеты, как может показаться дилетанту. Это условный параметр, вычисляемый по специальному калькулятору, размещённому во Всемирном информационном пространстве, уже определённый учёными и зафиксированный в специальных таблицах, или получаемый допотопными методами – собственноручными вычислениями по физической формуле.
Вычисления и формулы
Космические скорости Марса обусловлены его месторасположением, приближением во время годового оборота к разным по массе и расстоянию телам Вселенной, небольшой (по отношению к другим планетам) массой, наличием Фобоса и Деймоса. Поэтому в астрономии для чайников указывается средняя скорость.
Обратите внимание! Первая космическая скорость Марса, как и аналогичный параметр любого другого небесного тела – это ускорение, необходимое постороннему объекту, чтобы оторваться от поверхности планеты (звезды, спутника, астероида) и начать вращаться вокруг неё по круговой орбите, удалённой от поверхности на величину радиуса (половины диаметра) исследуемого объекта.
При этом, полученное от такого движения от поверхности, ускорение будет недостаточным для того, чтобы улететь от поверхности в окружающее пространство (по направлению к другому ближайшему или удалённому объекту), притяжения которого недостаточно для этого на Красной планете.
Первая космическая скорость Марса – это минимальное значение, определяемое расчётами. Есть и другие цифры величины перемещения в км и м в единицу времени, которых не будет хватать, чтобы оторваться и улететь в космос, продолжать оставаться на орбите, вращаясь, как Фобос и Деймос, в виде спутника, по траектории, заданной параметрами тела.
Первая космическая скорость Марса для расчётов потребует знания определённых параметров, уже давно определённых и зафиксированных учёными:
- массы загадочной планеты (М, она равна 6,4 * 10^23 кг);
- радиуса исследуемого небесного тела (R, 3,4 * 10^6 м);
- гравитационной постоянной (G, 6,67 * 10^-11 м^3/(кг*с^2).
V – искомый параметр, получается путём проведения вычислений:
Как данность, считается, что объект, запускаемый с планеты, стартует с его поверхности. Проведя вычисления, получаем ответ:
V = √ (G * M / R) = √ (6,67 * 10^-11 * 6,4 * 10^23 / (3,4 * 10^6)) = 3 543 м/с.
И ещё одна задача
Всего есть 3 искомых значения, и если первая позволяет объекту выйти на планетную орбиту, то вторая космическая скорость Марса – это характеристика, образно именуемая «скорость свободы». Именно так должен двигаться пленник красной планеты, который не хочет перманентно болтаться на орбите и намерен с неё улететь. Есть ещё и третья, необходимая, чтобы убыть из Солнечной системы. Она уменьшается по мере приближения к краям Вселенной и удаления от центра Солнечной системы.
Вторая космическая скорость Марса – 5,03 км/с, рассчитана уже давно, и, как и все вторые, позволяет улететь с орбиты небесного тела, разомкнув замкнутый круг вращения на орбите под действием его притяжения. Её особенность – движение по параболе, определение возможно, если есть данные о массе и радиусе. У Земли такая скорость в 2 раза больше, а для того, чтобы покинуть Солнце её придётся увеличить в несколько сотен раз.
Формула расчёта несколько отличается, но ненамного сложнее:
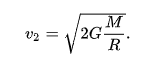
, где:
- v2 — вторая космическая скорость;
- R Марса, 3,4 * 10^6 м;
- g — Ускорение свободного падения у поверхности.
Простота и логичность вычислений доступны для всех, кто хорошо знаком со школьной программой физики. Марс – четвёртая по удалённости от Солнца, и вторая с конца, в ранжире по размеру планет Солнечной системы, планета, вокруг которой вращается сразу два спутника. На ней работают исследовательские станции, и обе расчётные величины используются в программе космических исследований.
Источник
Чему равна первая, вторая космическая скорость для Марса
Вычисление первой космической скорости на Марсе — задача несложная и описывается простыми физическими формулами. Именно эта скорость дает возможность летательному аппарату покинуть поверхность красной планеты и двигаться по ее орбите. А создание таких аппаратов — одна из важнейших целей в проектах по колонизации и исследованиям планеты Марс.
Даем определение космическим скоростям первой, второй
Чтобы ракета смогла попасть в космическое пространство, ей необходимо придать нужное ускорение и разогнать до скорости, которая позволит преодолеть силу земной гравитации.
Первая космическая скорость — это скорость, которую должен поддерживать объект, чтобы сохранять свое положение на орбите, двигаясь горизонтально над поверхностью планеты не снижаясь на нее и без ущерба для круговой траектории.
На Земле она составляет 7,9 километров в секунду. У Марса — меньше — 3,53 км в сек., так как масса Марса почти в два раза отличается от земной. Более подробно о расчетах этих величин расскажем ниже.
Но для межпланетных перемещений недостаточно вывести объект на орбиту. Нужно еще придать ему достаточный импульс, чтобы двигаться дальше, по параболе, полностью игнорируя силу планетного тяготения. Такая скорость считается 2-ой космо-скоростью. Другие ее названия — скорость освобождения, убегания или параболическая.
Вторая космическая скорость – это наименьшая скорость, которую должен развить объект, чтобы преодолеть силу притяжения центральной планеты и покинуть ее замкнутую орбиту.
Цифровые величины второй космической скорости для Марса, Земли равняются 5 км/с и 11,2 км/с соответственно.
Формулы вычисления этих двух космических скоростей получаются из основного закона классической теории тяготения Ньютона, который дает возможность с большой точностью рассчитать многие параметры и характеристики небесных объектов и звездных скоплений.
В результате изучения теории тяготения тел, установлено, что гравитационная сила притяжения двух объектов находится в прямой пропорциональности от масс этих тел и в обратной зависимости от расстояния между объектами:
F гр — это сила гравитации, m1, m2 — массы взаимодействующих тел, r — дистанция между ними. Важную роль в этой формуле имеет G — гравитационная постоянная:
Вычисление космических скоростей первой и второй
Для подсчета и определения первой космической скорости на Марсе воспользуемся уравнением движения, или II законом Ньютона:
В нашем примере F — сила притяжения, удерживающая тело на орбите, m — масса тела, a — его ускорение.
Ускорение при движении тела по окружности является центростремительным и равняется v2/r, где v — и есть 1-ая космическая скорость. В итоге после замены получаем формулу:
М — масса Марса, G — гравитационная константа, r — радиус орбиты.
Из этого равенства находим:
Зная массу Марса и другие величины, подставляем в формулу и получаем, что 1-ая космическая скорость Марса примерно равна:
v1 = 3,5 м/с = 3,53 км/с = 12728 км/ч = 2,2 мили/с = 7909 миль/ч
Продолжим расчет для второй космической скорости на Марсе. Формулу для нее получаем, пользуясь законом сохранения энергии, который описывает падение небесного объекта на планету из бесконечности:
Здесь r — радиус планеты, h — высота тела над планетой, M — масса Марса, G — гравитационный коэффициент, v — вторая космическая скорость.
Цифровое значение G стремительно мало и приводит к тому, что силы притяжения тел с маленькими массами, не ощутимы, что мы и наблюдаем у предметов на нашей планете Земле. Но для огромных астрономических тел гравитация и ее сила имеет первостепенное значение.
Решаем уравнение и находим v:
Таким образом, используя значения марсианских параметров, находим, что вторая космическая скорость для Марса составляет:
v2 = 5000 м/с = 18000 км/ч = 5 км/с = 3,11 мили/с = 11185 миль/ч
Соотношение обоих космических скоростей получается таким:
Кстати, если скорость летающего объекта имеет горизонтальное направление, по значению превышает 1-ую космическую, но меньше 2-ой космической, то тело будет двигаться по эллиптической орбите.
Формы орбит, по которым движутся улетающие объекты от планеты, представляют собой виды конических сечений:
- окружность — для тел, обладающих 1-ой;
- эллипс — при скорости, чуть меньше 2-ой;
- парабола — при 2-ой;
- гипербола — больше, чем 2-ая.
В школьных учебниках можно встретить множество интересных задач на космическую тематику. Многие из них начинаются словами: найдите вторую космическую скорость, вычислите значение первой для звезды, выведите формулу для расчета скорости летательного аппарата вокруг Марса и т.д.
Как вычислить нужные параметры и скорости — задачи типичные, и решаются с помощью выведенных выше формул.
Другие космические скорости — третья, четвертая и пятая
Кроме 1-ой и 2-ой космических скоростей (v1, v2) существуют и другие понятия — v3, v4 и v5. Все эти космические скорости — это скорости движения и характеристики летающих объектов или аппаратов в гравитационных полях астрономического пространства и действия небесных тел и систем — спутников, астероидов, звезд, комет, планет, галактик и звездных скоплений.
Все тела в космосе подчиняются закону всемирного тяготения, который был открыт одним из основоположников физики Исааком Ньютоном в 1666 году. Гравитация заставляет небесные тела притягиваться. Благодаря этим силам планеты удерживаются в системах, движутся вокруг звезд, а звезды собираются в галактики, формируя Вселенную. Кстати, физическая природа гравитации до сих не нашла полного объяснения. Механизм гравитационного взаимодействия до сих пор не разгадан учеными и не создана подходящая модель действия сил притяжения.
Критические космические скорости помогают ракетам и аппаратам вырваться из цепкого гравитационного влияния и отправиться в открытое пространство Вселенной. В результате их действия получается:
- v1 — предмет становится спутником небесного объекта, вращаясь на относительно небольшой высоте от его поверхности;
- v2 — в этом случае аппарат способен преодолеть силу гравитации и сможет удалиться от планеты;
- v3 — при таких скоростях аппарат уже может выйти за пределы не только гравитационного поля планеты, но и всей планетной системы (например, Солнечной), оторвавшись от притяжения центральной звезды;
- v4 — позволяет покинуть целую галактику;
- v5, v6 и тд. — понятие, можно сказать из области фантастики, скорость, которая позволяет улететь в любую точку любой другой галактики и даже Вселенной, уйти за пределы невиданной гравитации.
Первые две скорости помогают исследовать нашу солнечную систему и ее окрестности. Но их явно недостаточно, чтобы совершать путешествия свободно и быстро во всем космическом пространстве, которое раскрывается нам. Придет время, когда человечеству будут доступны другие сверхскорости. Но для этого нужно открыть иные источники дешевой энергии, а это пока за пределами наших возможностей.
Источник