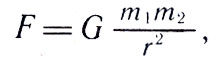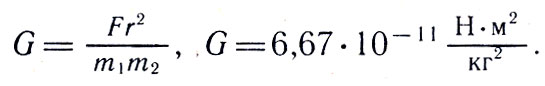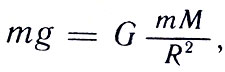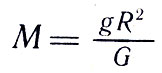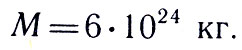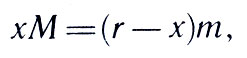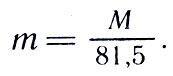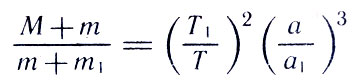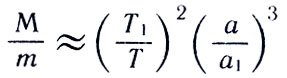Как взвесить землю луну

Как взвесить землю луну

Взвешивание Земли

Чтобы взвешивать планеты, прежде всего мы должны взвесить нашу Землю. Архимед сказал, что если бы у него была точка опоры, он мог бы сдвинуть Землю с помощью рычагов. С таким же успехом он мог бы взвесить Землю, наблюдая, насколько легко она сдвигается, когда он нажимает на рычаг. В действительности нам необходимо знать не вес Земли, но её массу. Вес тела есть только мера притяжения его Землёй, тогда как масса тела характеризует количество содержащейся в нём материи. Одно из великих открытий Ньютона заключалось в установлении факта, что вес тела пропорционален его массе. Если мы вернёмся к законам движения Ньютона, то увидим, что масса представляет собой меру силы, необходимой для изменения скорости движения тела на некоторую величину. Сдвинуть десятитонный вагон труднее, чем детскую коляску, вследствие разницы в массе. В пустом пространстве, где нет никаких притягивающих тел, ни вагон, ни детская коляска не будут иметь никакого веса, но массы их останутся неизменными.

Мы точно знаем, с какой силой действует притяжение Земли на единицу массы. Эта сила есть сила тяжести на поверхности Земли, которая притягивает нас к Земле и позволяет нам взвешивать различные предметы. Поскольку сила тяжести пропорциональна массе Земли, единственной неизвестной величиной является постоянная притяжения между двумя массами, так называемая постоянная тяготения ( Закон всемирного тяготения Ньютона утверждает, что два тела с массами m₁ и m₂, находящиеся на расстоянии r друг от друга, взаимно притягиваются с силой F=γm₁•m₂/r 2 , где γ — постоянная тяготения)).

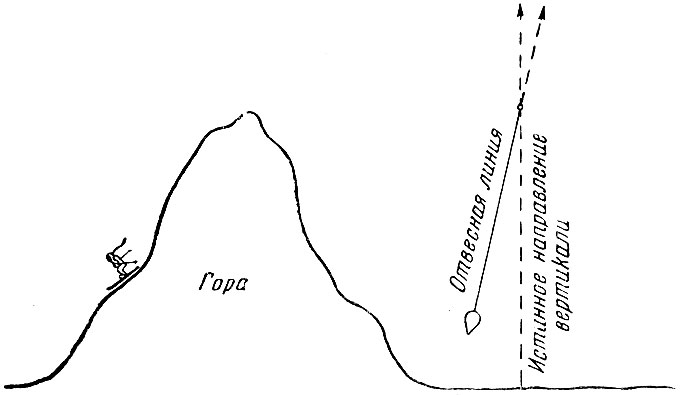
Один из методов определения этой постоянной заключается в измерении притяжения горы по отклонению линии отвеса. Как показано на рис. 30, линия отвеса направлена не строго вертикально, а отклонена от горы на некоторый угол, так как грузик отвеса притягивается к горе. Таким образом мы измеряем силу, с которой гора действует на грузик, и определяем массу горы, зная её размеры и составляющие её породы. Поскольку расстояние до горы измерить легко, мы имеем все данные для вычисления постоянной тяготения, а следовательно, и массы Земли.

Рис. 30. Гора притягивает свинцовый грузик. Направление отвеса отклоняется от вертикали, давая меру притяжения горы

Описанный метод весьма прост, но менее точен, чем лабораторные методы. С помощью весьма чувствительных инструментов можно непосредственно измерить притяжение, которое оказывает большой свинцовый шар на такой же шар меньших размеров, и таким образом получить значение постоянной тяготения. Поскольку вес малого шара измеряет величину притяжения его Землёй, массу Земли можно выразить в массах большого шара, применяя закон тяготения. Если бы Землю можно было положить на весы на её поверхности, то она весила бы 6 600 000 000 000 000 000 000 т.

Сила тяготения, есть лишь небольшое отклонение от отсутствия всякой силы; она становится заметной, лишь когда мы имеем дело с огромными количествами материи. Представим себе шар, сделанный из всего золота добытого во всём мире, скажем, 30000 т; такой шар имел бы 14 м в диаметре. Если бы этот шар находился в пространстве, вдали от всех притягивающих сил, то человек весом 80 кг, сидящий на нём, весил бы столько же, сколько 0,3 г на Земле. Сверчок легко мог бы поднять этого человека, а лягушка могла бы вообще сбросить его с золотого шара. Поскольку обычно человека не так легко отогнать от золота, мы можем заключить, подобно Эзопу, что сила скупости значительно превосходит силу тяготения.

Источник

Как взвесить землю луну

Как взвесить Солнце?

В повседневной жизни тяготение тел друг к другу (кроме силы тяжести) неощутимо. Слишком ничтожно мала гравитация (т. е. тяготение) по сравнению с другими силами. Лишь исполинские массы Земли и других космических тел создают иллюзию мощности тяготения. Но только очень тонкими экспериментами удается измерить, как притягивают друг друга небольшие тела.

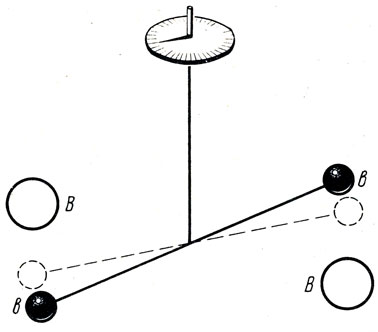
Первый успешный опыт такого рода был проделан еще в 1798 г. соотечественником Ньютона Г. Кавендишем (1731-1810). Его установка, получившая название крутильных весов (рис. 34), состояла из двух маленьких шариков (в), соединенных стержнем, который подвешивался на кварцевой нити. Вблизи этих шариков Кавендиш помещал два массивных свинцовых шара (В). Эти шары, притягивая концы стержня, закручивали кварцевую нить. По закручиванию нити можно вычислить силу притяжения F. По закону тяготения

где m₁ и m₂ — массы маленьких шариков, r — расстояние между ними и большими шарами, a G — коэффициент пропорциональности, называемый постоянной тяготения, значение которого можно определить из указанной формулы:

Рис. 34. Крутильные весы Кавендиша

Зная G и используя закон тяготения, можно определить массу Земли и других космических тел. В самом деле, пусть масса Земли М. Тогда любое тело массой т притягивается Землей с силой

где R — радиус Земли. Отсюда масса земного шара равна

Подставив в формулу известное значение величин, получим

По закону тяготения Земля и Луна обращаются вокруг общего центра тяжести С, который лежит внутри Земли. Обозначим его расстояние до центра Земли буквой х. Тогда по законам механики

где М — масса Земли, m — масса Луны, а r — расстояние между ними. Из-за движения Земли вокруг точки С меняется астрономическая долгота Солнца (по сравнению с той, которая была бы при отсутствии такого движения). Точные астрономические измерения приводят к выводу, что х = 4635 км и, следовательно,

«Взвесив» Луну, или, точнее говоря, определив ее массу, можно перейти к «взвешиванию» Солнца. Пусть некоторая планета массой т имеет спутник массой m₁. Массу Солнца обозначим М, а периоды обращения планеты вокруг Солнца и спутника вокруг планеты соответственно Т и T₁. Тогда по уточненному третьему закону Кеплера следует:

где а и a₁ — полуоси орбит планеты и спутника. Так как масса планеты мала по сравнению с массой Солнца, а у спутника много меньше, чем у планеты, приходим к приближенному равенству

Используя в качестве планеты и ее спутника Землю и Луну, получаем, что масса Солнца примерно в 333 000 раз больше массы Земли, т. е. масса Солнца приблизительно равна 2*10 30 кг.

Описанные методы «взвешивания» небесных тел не всегда применимы и далеко не единственны. Но любые иные методы в конечном счете основываются на законе всемирного тяготения: неизвестную массу тела находят по гравитационному воздействию этого тела на другие тела.

Источник

Как взвесили Землю

Как взвесили Землю

Прежде всего необходимо объяснить смысл выражения: «взвесить Землю». Ведь если бы даже было возможно взвалить земной шар на какие-нибудь весы, то где же весы эти установить? Когда мы говорим о весе какой-нибудь вещи, то в сущности речь идет о той силе, с какой вещь эта притягивается Землей или стремится падать к Земле, к ее центру. Но сама-то наша Земля не может же падать на себя! Поэтому говорить о весе земного шара бессмысленно, пока не установлено, что надо понимать под этими словами.

Смысл слов «вес Земли» может быть только таков. Вообразите, что из Земли вырезали куб в метр вышины и взвесили. Вес этого куба записали, а сам куб поместили на прежнее место; потом вырезали соседний кубический метр и тоже взвесили. Записав вес второго куба, установили его на свое место и вырезали третий. Если перебрать так один за другим все кубические метры, из которых состоит наша планета, взвесить их поодиночке, а затем все их веса сложить, мы узнаем, сколько весит все вещество, составляющее земной шар. Короче сказать, поступая указанным образом, мы взвесили бы Землю.

Само собою разумеется, что на деле выполнить такую работу немыслимо. Если бы мы даже могли изрыть всю поверхность земного шара, то забраться в его недра мы не в силах. Нигде еще человек не вкапывался в землю глубже 4 километров, – а ведь до центра земного шара свыше 6 000 километров… Значит ли это, что людям надо отказаться от надежды узнать вес своей планеты? Существует, однако, косвенный путь для взвешивания земного шара. Ученые пошли по этому пути и достигли полного успеха. Вот в чем состоит этот косвенный путь. Мы знаем, что вес вещи есть сила, с какою эта вещь притягивается Землею. Один кубический сантиметр воды притягивается Землею с силой одного грамма (ведь он весит один грамм). Если мы возьмем не кубический сантиметр воды, а кубический метр воды, заключающий воды в миллион раз больше, то он будет притягиваться в миллион раз сильнее: его вес будет 1 000 000 граммов, т. е. одна тонна. Но притяжение между взвешиваемою вещью и Землею зависит также от количества материи в ней, и если бы наша планета заключала в себе вещества в миллион раз больше, один грамм весил бы на такой Земле целую тонну. И наоборот, если бы Земля заключала в миллион раз меньше вещества, она притягивала бы все вещи во столько же раз слабее, и тогда один грамм весил бы на такой планете только миллионную долю грамма.

Косвенный путь взвешивания Земли состоял в том, что ученые изготовили как бы крошечную Землю и измерили, с какою силою она притягивает к себе 1 грамм вещества. Сделано это было примерно так. К одной чашке очень чувствительных и точных весов подвешивается шарик, и весы уравновешиваются гирей, поставленной на другую чашку. Затем под первую чашку подводят большой свинцовый шар, вес которого точно известен. При этом оказывается, что весы выходят из равновесия: большой шар притягивает к себе маленький шарик, подвешенный к чашке весов и заставляет ее опускаться. Чтобы снова уравновесить весы, нужно на другую чашку положить небольшой добавочный грузик. Этот добавочный грузик и измеряет ту силу, с какой большой шар притягивает к себе маленький. Мы можем теперь сказать, во сколько раз сила притяжения земного шара больше, чем сила притяжения свинцового шара. Но это еще не значит, что во столько же раз Земля тяжелее свинцового шара: надо принять в расчет и то, что подвешенный шарик отстоит от центра Земли на 6 400 километров, а от центра свинцового шара – всего только на несколько сантиметров. Ученым в точности известно, как ослабевает сила взаимного притяжения с увеличением расстояния; поэтому они смогли учесть влияние различия расстояния в нашем случае и определить, во сколько именно раз земной шар заключает в себе больше килограммов вещества, чем свинцовый. Короче сказать, они могли узнать, сколько весит Земля. А именно: узнали, что Земля весит круглым числом шесть тысяч миллионов миллионов миллионов тонн:

6 000 000 000 000 000 000 000 тонн.

Если бы мы отвешивали такую массу на весах и каждую секунду клали на чашку миллион тонн, то знаете, сколько времени должны были бы мы безостановочно, день и ночь, работать, чтобы закончить такое отвешивание? Двести миллионов лет! А ведь один миллион тонн во много раз тяжелее самых тяжелых сооружений, возведенных руками человека. Эйфелева башня весит всего 9 000 тонн, а корабли-исполины – линкоры и плавающие пассажирские дворцы – не тяжелее 30–50 тысяч тонн.

Тем удивительнее должна нам казаться научная изобретательность человека, который сумел измерить этот чудовищный груз, сумел взвесить ту планету, на которой он живет.

Конечно, в действительности опыт был обставлен не так просто, как мы изобразили. Чтобы сделать его суть понятнее, нам пришлось упростить его, отбросив все подробности. Притяжение свинцового шара настолько слабо, что для его обнаружения и измерения потребовался целый набор очень точных и сложных инструментов, устройство которых представляет интерес только для тех, кто намерен и имеет возможность сам повторить этот опыт.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

С неба на землю

С неба на землю Радость видеть и понимать есть самый прекрасный дар природы. Эйнштейн Загадка небесной лазуриПочему небо голубое. Нет такого человека, который не задумался над этим хоть раз в жизни.Объяснить происхождение цвета неба старались уже средневековые

ОТКРЫТИЕ НЕОЖИДАННЫХ СВОЙСТВ АТМОСФЕРЫ — СТРАННЫЕ ЭКСПЕРИМЕНТЫ — ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПО ОДНОМУ ПРОВОДУ БЕЗ ВОЗВРАТНОГО — ПЕРЕДАЧА ЧЕРЕЗ ЗЕМЛЮ ВООБЩЕ БЕЗ ПРОВОДОВ

ОТКРЫТИЕ НЕОЖИДАННЫХ СВОЙСТВ АТМОСФЕРЫ — СТРАННЫЕ ЭКСПЕРИМЕНТЫ — ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПО ОДНОМУ ПРОВОДУ БЕЗ ВОЗВРАТНОГО — ПЕРЕДАЧА ЧЕРЕЗ ЗЕМЛЮ ВООБЩЕ БЕЗ ПРОВОДОВ Другая из этих причин в том, что я пришел к осознанию того, что передача электрической энергии

С небес на землю и обратно

С небес на землю и обратно В современной физике говорят о четырех фундаментальных силах. Первой открыли силу гравитации. Известный школьникам закон всемирного тяготения определяет силу притяжения F между любыми массами m и M, разделенными расстоянием R:F = G mM/R2.Школьникам

ВЕРНЕМСЯ НА ЗЕМЛЮ

ВЕРНЕМСЯ НА ЗЕМЛЮ Теория струн, скорее всего, содержит немало глубоких и перспективных идей. Она уже помогла нам заглянуть краешком глаза во владения квантовой гравитации и математики и обеспечила интересными ингредиентами для построения новых моделей. Но, скорее всего,

15. Что делает Землю особенной?

15. Что делает Землю особенной? Три причины: жизнь, жизнь, жизнь. Земля — единственная планета, которая может похвастаться биологией. Но она имеет также и другие особые свойства, возможно, относящиеся к жизни.Из четырех скалистых планет Солнечной системы Земля —

25. Как Луна влияет на Землю?

25. Как Луна влияет на Землю? Два раза в день море надвигается на пляжи, а затем отступает. Такие приливы, которые впервые объяснил Исаак Ньютон, вызваны Луной.Вопреки распространенному мнению, приливы на Земле вызваны не столько гравитацией Луны, сколько изменениями в

Глава 8 Последствия падений крупных небесных тел на землю

Глава 8 Последствия падений крупных небесных тел на землю Кто что ни говори, а подобные происшествия бывают на свете, — редко, но бывают. Н. В. Гоголь. «Нос» Последствия падений крупных тел на Землю в целом известны. Мы будем рассматривать только те, которые можно

Источник