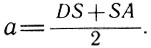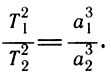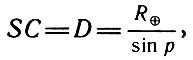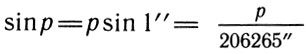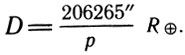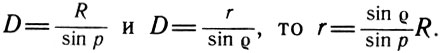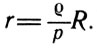§ 117. Законы движения планет
В конце XVI в. датский астроном И. Кеплер, изучая движение планет, открыл три закона их движения. На основании этих законов И. Ньютон вывел формулу для закона всемирного тяготения. В дальнейшем, используя законы механики, И. Ньютон решил задачу двух тел — вывел законы, по которым одно тело движется в поле тяготения другого тела. Он получил три обобщенных закона Кеплера.
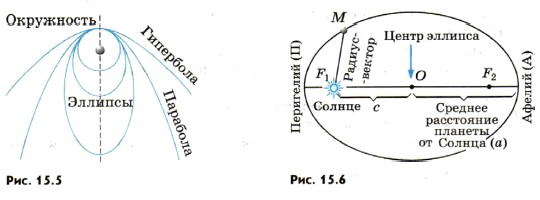
Первый закон Кеплера. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе (рис. 15.5).
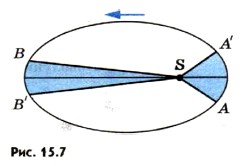
Планеты движутся вокруг Солнца по эллиптической орбите (рис. 15.6). Ближайшая к Солнцу точка орбиты называется перигелием, самая далекая — афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором. Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. Эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а — среднее расстояние планеты до Солнца.
По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 1 (см. рис. 15.5).
Движение естественных и искусственных спутников вокруг планет, движение одной звезды вокруг другой в двойной системе также подчиняются этому первому обобщенному закону Кеплера.
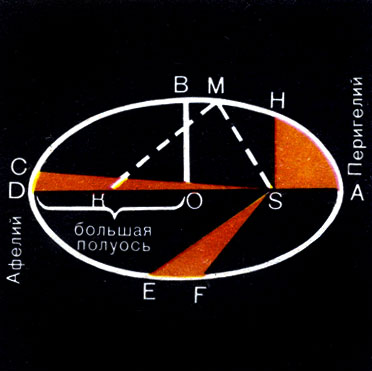
Второй закон Кеплера. Каждая планета движется так, что радиус-вектор планеты за равные промежутки времени описывает равные площади.
Планета проходит путь от точки А до А’ и от В до В’ (рис. 15.7) за одно и то же время. Другими словами, планета движется быстрее всего в перигелии, а медленнее всего — когда находится на наибольшем удалении (в афелии). Таким образом, второй закон Кеплера определяет скорость движения планеты. Она тем больше, чем планета ближе к Солнцу. Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с.
Третий закон Кеплера. Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная.
Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как
где М1 и М2 — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца 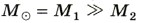
Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений.
Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит.
Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них.
Вопросы к параграфу
1. Перечислите основные элементы эллиптической орбиты планеты.
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
Источник
Решебник по физике за 11 класс Мякишев: вопросы к параграфам 59-125
Вопрос 117.
1. Перечислите основные элементы эллиптической орбиты планеты?
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
1. Планеты движутся вокруг Солнца по эллипсам. Ближайшая к Солнцу точка орбиты называется перигелием, самая удаленная — афелием. Вектор, проведенный из некоторой точки эллипса в фокус, называется радиус-вектором. Отношение расстояния между фокусами к длине большой оси эллипса, называется эксцинтриситетом.
2. Квадраты периодов обращения двух планет относятся как кубы средних расстояний до Солнца.
3. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе.
4. Третий закон Кеплера:


а — среднее расстояние между телами, Т — период обращения одного тела относительно другого, G — гравитационная постоянная.
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже 👇
Вы получите: 🎭 Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
или пишите «Хочу бесплатные шаблоны» в директ Инстаграм @shablonoved.ru
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже 👇
Вы получите: 🎭 Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
Источник
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
6. Выполните задание.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Законы движения планет
Третий закон Кеплера. Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная.
Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как
где М1 и М2 — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца 
Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений.
Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит.
Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них.
Вопросы к параграфу
1. Перечислите основные элементы эллиптической орбиты планеты.
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
Источник
Как связаны периоды обращения планет с их средними расстояниями до солнца
11. Законы Кеплера
Иоганн Кеплер (1571-1630). Выдающийся немецкий астроном и математик, открывший законы движения планет вокруг Солнца. Кеплер был активным сторонником учения Коперника и своими работами способствовал его утверждению и развитию
Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну Кеплеру (1571-1630). В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.
Первый закон Кеплера. Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 30).
Рис. 30. Закон площадей (второй закон Кеплера)
Эллипсом (см. рис. 30) называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной. Эта сумма расстояний равна длине большой оси DA эллипса. Точка О — центр эллипса, К и S — фокусы. Солнце находится в данном случае в фокусе S. DO=OA=a — большая полуось эллипса. Большая полуось является средним расстоянием планеты от Солнца:
Ближайшая к Солнцу точка орбиты А называется перигелием, а самая далекая от него точка D — афелием.
Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет равен отношению расстояния фокуса от центра (OK=OS) к длине большой полуоси а, т. е. 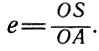
Орбиты планет — эллипсы, мало отличающиеся от окружностей; их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е=0,017.
Второй закон Кеплера (закон площадей). Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади, т. е. площади SAH и SCD равны (см. рис. 30), если дуги 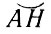
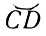
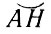
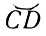
Третий закон Кеплера. Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит. Если большую полуось орбиты и звездный период обращения одной планеты обозначить через a1,T1, а другой планеты — через а2, Т2, то формула третьего закона будет такова:
Этот закон Кеплера связывает средние расстояния планет от Солнца с их звездными периодами и позволяет установить относительные расстояния планет, от Солнца, поскольку звездные периоды планет уже были вычислены, исходя из синодических периодов, иначе говоря, позволяет выразить большие полуоси всех планетных орбит в единицах большой полуоси земной орбиты.
Большая полуось земной орбиты принята за астрономическую единицу расстояний (а
Ее значение в километрах было определено позднее, лишь в XVIII в.
Пример решения задачи
Задача. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?
Упражнение 8
1. Марс дальше от Солнца, чем Земля, в 1,5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
2. Определите период обращения искусственного спутника Земли, если наивысшая точка его орбиты над Землей 5000 км, а наинизшая 300 км. Землю считать шаром радиусом 6370 км. Сравните движение спутника с обращением Луны.
3. Синодический период планеты 500 сут. Определите большую полуось ее орбита и звездный период обращения.
12. Определение расстояний и размеров тел в солнечной системе
1. Определение расстояний
Среднее расстояние всех планет от Солнца в астрономических единицах можно вычислить, используя третий закон Кеплера. Определив среднее расстояние Земли от Солнца (т. е. значение 1 а. е.) в километрах, можно найти в этих единицах расстояния до всех планет Солнечной системы.
С 40-х годов нашего века радиотехника позволила определять расстояния до небесных тел посредством радиолокации, о которой вы знаете из курса физики. Советские и американские ученые уточнили радиолокацией расстояния до Меркурия, Венеры, Марса и Юпитера.
Вспомните, как по времени прохождения радиолокационного сигнала можно определить расстояние до объекта.
Классическим способом определения расстояний был и остается угломерный геометрический способ. Им определяют расстояния и до далеких звезд, к которым метод радиолокации неприменим. Геометрический способ основан на явлении параллактического смещения.
Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя (рис. 31).
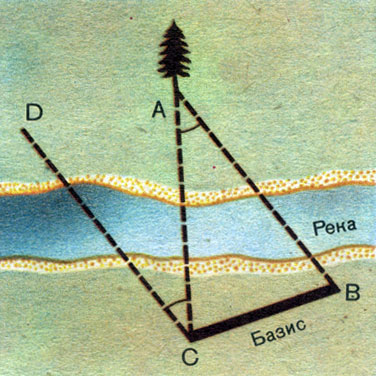
Рис. 31. Измерение расстояния до недоступного предмета по параллактическому смещению
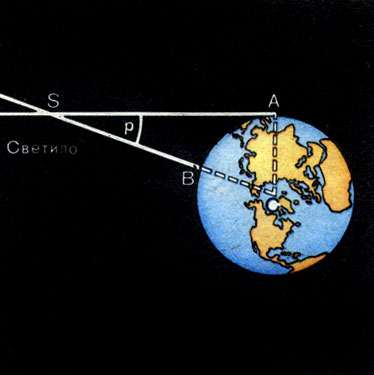
Посмотрите на вертикально поставленный карандаш сначала одним глазом, затем другим. Вы увидите, как он при этом переменил положение на фоне далеких предметов, направление на него изменилось. Чем дальше вы отодвинете карандаш, тем меньше будет параллактическое смещение. Но чем дальше отстоят друг от друга точки наблюдения, т. е. чем больше базис, тем больше параллактическое смещение при той же удаленности предмета. В нашем примере базисом было расстояние между глазами. Для измерения расстояний до тел Солнечной системы за базис удобно взять радиус Земли. Наблюдают положения светила, например Луны, на фоне далеких звезд одновременно из двух различных пунктов. Расстояние между ними должно быть как можно больше, а соединяющий их отрезок должен составлять с направлением на светило угол, по возможности близкий к прямому, чтобы параллактическое смещение было максимальным. Определив из двух точек А и В (рис. 32) направления на наблюдаемый объект, несложно вычислить угол р, под которым с этого объекта был бы виден отрезок, равный радиусу Земли. Следовательно, чтобы определить расстояния до небесных тел, нужно знать значение базиса — радиуса нашей планеты.
Рис. 32. Горизонтальный параллакс светила
2. Размер и форма Земли
На фотоснимках, сделанных из космоса, Земля выглядит как шар, освещенный Солнцем, и показывает такие же фазы, как Луна (см. рис. 42 и 43).
Точный ответ о форме и размере Земли дают градусные измерения, т. е. измерения в километрах длины дуги в 1° в разных местах на поверхности Земли. Этот способ еще в III в, до н. э. применял живший в Египте греческий ученый Эратосфен. Теперь этот способ используется в геодезии — науке о форме Земли и об измерениях на Земле с учетом ее кривизны.
На ровной местности выбирают два пункта, лежащие на одном меридиане, и определяют длину дуги между ними в градусах и километрах. Затем вычисляют, скольким километрам соответствует длина дуги, равная 1°. Ясно, что длина дуги меридиана между выбранными точками в градусах равна разности географических широт этих точек: Δφ= = φ1 — φ2. Если длина этой дуги, измеренная в километрах, равна l, то при шарообразности Земли одному градусу (1°) дуги будет соответствовать длина в километрах: 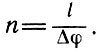
Одна из наибольших дуг меридиана от Ледовитого океана до Черного моря была измерена в России и в Скандинавии в середине XIX в. под руководством В. Я. Струве (1793-1864), директора Пулковской обсерватории. Большие геодезические измерения в нашей стране выполнены после Великой Октябрьской социалистической революции.
Градусные измерения показали, что длина 1° дуги меридиана в километрах в полярной области наибольшая (111,7 км), а на экваторе наименьшая (110,6 км). Следовательно, на экваторе кривизна поверхности Земли больше, чем у полюсов, а это говорит о том, что Земля не является шаром. Экваториальный радиус Земли больше полярного на 21,4 км. Поэтому Земля (как и другие планеты) вследствие вращения сжата у полюсов.
Шар, равновеликий нашей планете, имеет радиус, равный 6370 км. Это значение принято считать радиусом Земли.
Упражнение 9
1. Если астрономы могут определять географическую широту с точность до 0,1″, то какой максимальной ошибке в километрах вдоль меридиана это соответствует?
2. Вычислите в километрах длину морской мили, которая равна длине V дуги экватора.
3. Параллакс. Значение астрономической единицы
Угол, под которым со светила виден радиус Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом.
Чем больше расстояние до светила, тем меньше угол ρ. Этот угол равен параллактическому смещению светила для наблюдателей, находящихся в точках А и В (см. рис. 32), точно так же как ∠CAB для наблюдателей в точках С и В (см. рис. 31). ∠CAB удобно определять по равному ему ∠DCA, а равны они как углы при параллельных прямых (DC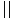
Расстояние (см. рис. 32)
где R
Горизонтальный параллакс Луны составляет 57′. Все планеты и Солнце гораздо дальше, и их параллаксы составляют секунды дуги. Параллакс Солнца, например, ρ
При малых углах sinρ≈ρ, если угол ρ выражен в радианах. Если ρ выражен в секундах дуги, то вводится множитель 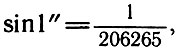
Тогда
Знание этих соотношений упрощает вычисление расстояния по известному параллаксу:
Пример решения задачи
Задача. На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9″?
Упражнение 10
1. Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля?
2. Расстояние Луны от Земли в ближайшей к Земле точке орбиты (перигее) 363 000 км, а в наиболее удаленной точке (апогее) 405 000 км. Определите горизонтальный параллакс Луны в этих положениях.
4. Определение размеров светил
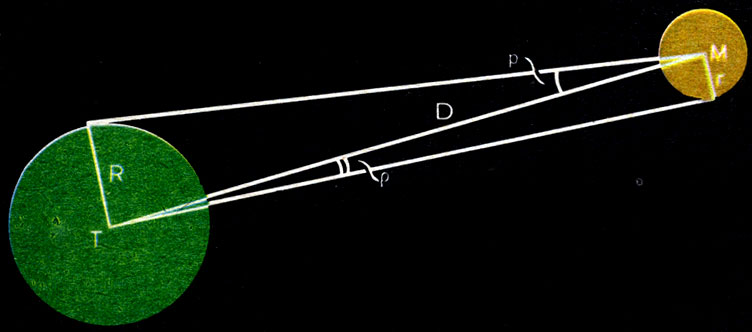
На рисунке 33 Т — центр Земли, М — центр светила линейного радиуса r. По определению горизонтального параллакса радиус Земли R виден со светила под углом ρ. Радиус же светила r виден с Земли под углом 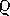
Если углы 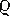
Этот способ определения размеров светил применим только тогда, когда виден диск светила.
Зная расстояние D до светила и измерив его угловой радиус 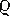
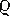
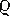
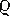
Пример решения задачи
Задача. Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 0,5°?
Упражнение 11
1. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы соответственно равны 8,8″ и 57′?
2. Чему равен угловой диаметр Солнца, видимого с Плутона?
3. Во сколько раз больше получает энергии от Солнца каждый квадратный метр поверхности Меркурия, чем Марса? Нужные данные возьмите из приложений.
4. В каких точках небосвода земной наблюдатель видит светило, находясь в точках B и A (рис. 32)?
5. В каком отношении численно меняется видимый с Земли и с Марса угловой диаметр Солнца от перигелия к афелию, если эксцентриситеты их орбит соответственно равны 0,017 и 0,093?
Задание 5
1. Измерьте транспортиром ∠DCA (рис. 31) и ∠ASC (рис. 32), линейкой — длину базисов. Вычислите по ним соответственно расстояния СА и SC и проверьте результат прямым измерением по рисункам.
2. Измерьте на рисунке 33 транспортиром углы р и 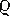
3. Определите периоды обращения искусственных спутников, двигающихся по эллиптическим орбитам, изображенным на рисунке 34, измерив их большие оси линейкой и приняв радиус Земли равным 6370 км.
Рис. 33. Определение линейных размеров небесных светил по их угловым размерам
Источник