Решебник по физике за 11 класс Мякишев: вопросы к параграфам 59-125
Вопрос 117.
1. Перечислите основные элементы эллиптической орбиты планеты?
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
1. Планеты движутся вокруг Солнца по эллипсам. Ближайшая к Солнцу точка орбиты называется перигелием, самая удаленная — афелием. Вектор, проведенный из некоторой точки эллипса в фокус, называется радиус-вектором. Отношение расстояния между фокусами к длине большой оси эллипса, называется эксцинтриситетом.
2. Квадраты периодов обращения двух планет относятся как кубы средних расстояний до Солнца.
3. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе.
4. Третий закон Кеплера:


а — среднее расстояние между телами, Т — период обращения одного тела относительно другого, G — гравитационная постоянная.
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже 👇
Вы получите: 🎭 Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
или пишите «Хочу бесплатные шаблоны» в директ Инстаграм @shablonoved.ru
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже 👇
Вы получите: 🎭 Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
Источник
§ 117. Законы движения планет
В конце XVI в. датский астроном И. Кеплер, изучая движение планет, открыл три закона их движения. На основании этих законов И. Ньютон вывел формулу для закона всемирного тяготения. В дальнейшем, используя законы механики, И. Ньютон решил задачу двух тел — вывел законы, по которым одно тело движется в поле тяготения другого тела. Он получил три обобщенных закона Кеплера.
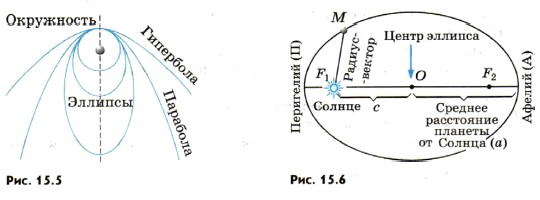
Первый закон Кеплера. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе (рис. 15.5).
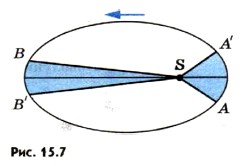
Планеты движутся вокруг Солнца по эллиптической орбите (рис. 15.6). Ближайшая к Солнцу точка орбиты называется перигелием, самая далекая — афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором. Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. Эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а — среднее расстояние планеты до Солнца.
По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 1 (см. рис. 15.5).
Движение естественных и искусственных спутников вокруг планет, движение одной звезды вокруг другой в двойной системе также подчиняются этому первому обобщенному закону Кеплера.
Второй закон Кеплера. Каждая планета движется так, что радиус-вектор планеты за равные промежутки времени описывает равные площади.
Планета проходит путь от точки А до А’ и от В до В’ (рис. 15.7) за одно и то же время. Другими словами, планета движется быстрее всего в перигелии, а медленнее всего — когда находится на наибольшем удалении (в афелии). Таким образом, второй закон Кеплера определяет скорость движения планеты. Она тем больше, чем планета ближе к Солнцу. Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с.
Третий закон Кеплера. Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная.
Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как
где М1 и М2 — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца 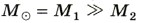
Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений.
Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит.
Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них.
Вопросы к параграфу
1. Перечислите основные элементы эллиптической орбиты планеты.
2. Как связаны периоды обращения планет с их средними расстояниями до Солнца?
3. Сформулируйте первый обобщенный закон Кеплера.
4. Запишите третий обобщенный закон Кеплера.
Источник
Как связаны период обращения планет с их средними расстояниями до солнца
Цель работы: изучение движения тел под действием сил тяготения; проверка третьего закона Кеплера.
На смену геоцентрической системе мира, созданной в начале нашей эры Птолемеем, пришла гелиоцентрическая система, созданная Коперником. Несколько позднее немецкий астроном И. Кеплер на основе астрономических наблюдений установил законы движения планет вокруг Солнца.
Согласно 1-му закону Кеплера любая планета движется вокруг Солнца по замкнутой кривой, которая называется эллипсом (внешне похож на овал). Солнце находится в одном из фокусов этого эллипса. Эллипс имеет два фокуса: это две такие точки внутри кривой, сумма расстояний от которых до произвольной точки эллипса постоянна. Оказывается, что орбиты всех планет Солнечной системы лежат примерно в одной плоскости. Большинство планет движутся по орбитам-эллипсам, которые близки к окружностям. Лишь Марс и Плутон имеют сравнительно вытянутые орбиты.
Второй закон Кеплера устанавливает, что скорость планеты больше тогда, когда она в своем движении находится ближе к Солнцу (в так называемой точке перигелия) и меньше тогда, когда она находится на наибольшем расстоянии от Солнца (в точке афелия). Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и ее средним расстоянием от Солнца, он применяется ко всему коллективу планет Солнечной системы.
Законы Кеплера получили свое объяснение лишь после открытия законов тяготения. Физические объекты участвуют в гравитационном взаимодействии, т.е. они притягиваются друг к другу. Гравитационное взаимодействие обладает всеобщей универсальностью: ему подвержены все материальные объекты и даже физические поля. Закон всемирного тяготения был открыт И. Ньютоном. Он утверждает, что два неподвижных точечных тела взаимодействуют друг с другом с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними, т.е.
 , , | (1) |
где γ называют гравитационной постоянной. Этот закон справедлив и для взаимодействия однородных шаров, но в этом случае под r следует понимать расстояние между их центрами.

Отсюда получаем, что 


 . . | (2) |
Это и есть третий закон Кеплера, который можно сформулировать следующим образом: отношение куба расстояния от планеты до Солнца к квадрату периода ее обращения вокруг Солнца есть величина постоянная, одинаковая для всех планет Солнечной системы. В случае движения по эллипсу, когда расстояние от планеты до Солнца при движении изменяется, в законе фигурирует некоторое среднее расстояние, т.е. полусумма максимального и минимального расстояний от данной планеты до Солнца. Закон Кеплера справедлив для любой планетной системы, а также для системы спутников какой-либо конкретной планеты, например, для системы спутников Юпитера или Урана. В последнем случае под М в формуле (2) понимается масса соответственно Юпитера или Урана.
Источник
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
вкл. 27 Ноябрь 2016 .
Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
6. Выполните задание.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Источник
Как связаны период обращения планет с их средними расстояниями до солнца
§ 11. К онфигурация планет. С инодический период
1. Конфигурация планет и условия их видимости
У словия видимости планет Подробные сведения о положении планет и условиях их видимости даются в «Школьном астрономическом календаре» на каждый учебный год. Эту информацию можно найти и в Интернете. меняются по-разному: если Меркурий и Венеру можно видеть только утром или вечером, то остальные — Марс, Юпитер и Сатурн — бывают видны также и ночью. По временам одна или несколько планет могут быть вовсе не видны, поскольку они располагаются на небе поблизости от Солнца. В этом случае говорят, что планета находится в соединении с Солнцем. Если же планета располагается на небе вблизи точки, диаметрально противоположной Солнцу, то она находится в противостоянии . В этом случае планета появляется над горизонтом в то время, когда Солнце заходит, а заходит она одновременно с восходом Солнца. Следовательно, всю ночь планета находится над горизонтом.
Соединение и противостояние, а также другие характерные расположения планеты относительно Солнца называются конфигурациями . Внутренние планеты (Меркурий и Венера), которые всегда находятся внутри земной орбиты, и внешние, которые движутся вне её (все остальные планеты), меняют свои конфигурации по-разному. Названия различных конфигураций внутренних и внешних планет, которые характеризуют расположение планеты относительно Солнца на небе, приведены в таблице и на рисунке 3.4.
Рис. 3.4. Конфигурации внутренней и внешней планеты
Источник